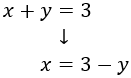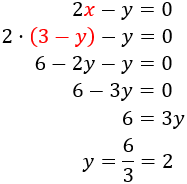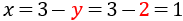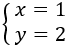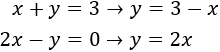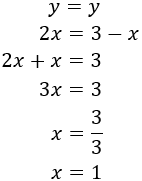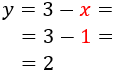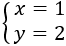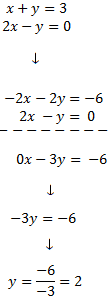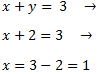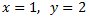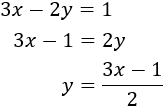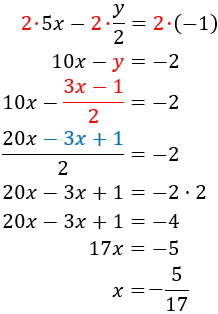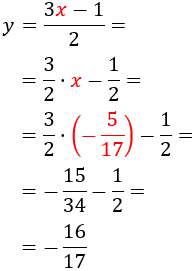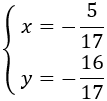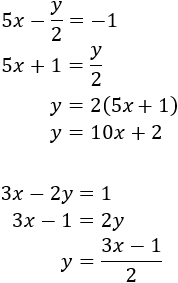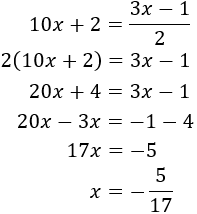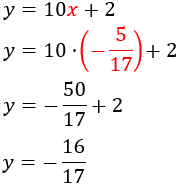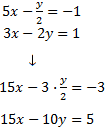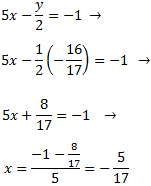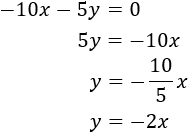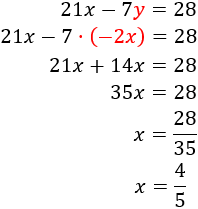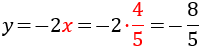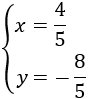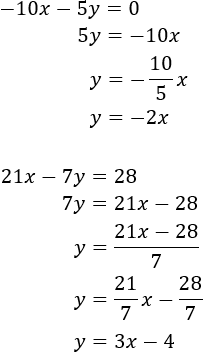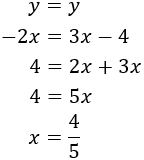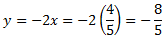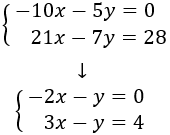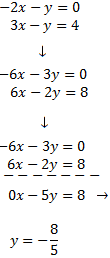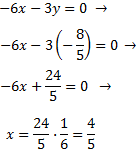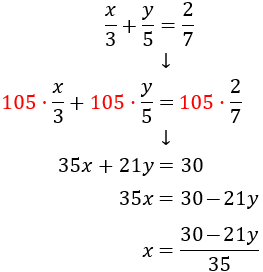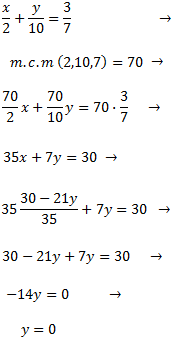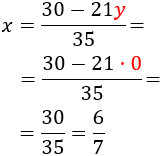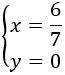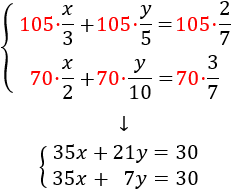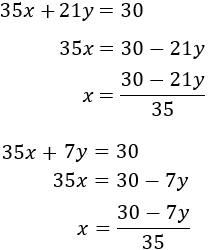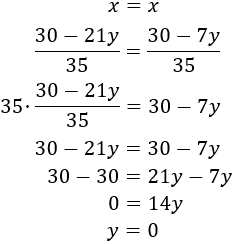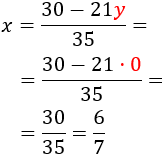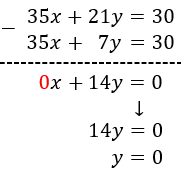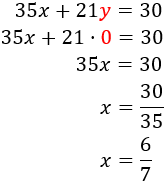Solving a System of Linear Equations |
Content of this page:
-
Introduction
-
The methods
-
4 resolved systems of linear equations by substitution, addition and equalization
Introduction
A system of linear equations (or linear system) is a group of (linear) equations that have more than one unknown factor. The unknown factors appear in various equations, but do not need to be in all of them. What these equations do is to relate all the unknown factors amongt themselves. For example,
$$\left\{ \begin{eqnarray} 3x+2y=1 \\ x-5y=6 \end{eqnarray} \right. $$is an equation system with two equations with two unknown factors (x and y).
Solving this type of problems (a system) consists in finding a value for each unknown factor in a way that it applies to all the equations in the system. The solution of the example system is:
$$ \begin{eqnarray} x=1 \\ y=-1 \end{eqnarray}$$There is not always a solution and even there could be an infinite number of solutions. If there is only one solution (one value for each unknown factor, like in the previous example), the system is said to be a consistent dependent system. We will not speak about other kinds of systems.
To solve consistent dependent a system, we need at least the same number of equations as unknown factors. In this section we will resolve linear systems of two equations and two unknown factors with the methods we describe next, which are based on obtaining a first degree equation (a linear equation).
The methods
-
Substitution (elimination of variables): It consists in isolating one of the unknown factors (for example x) and substitute that expression in the other equation. Thus a first degree equation with the unknown factor y is obtained. Once resolved, we obtain the value of x using the value of y we know.
-
Elimination: It consists in operating the equations, for example, adding or subtracting both equations so one of the unknown factors disappears. Thus an equation with only one known factor is obtained.
Equalization: It consists in isolating from both equations the same unknown factor to be able to equal both expressions, obtaining one equation with one unknown factor.
Let us not forget that if we multiply an equation by a number different from 0, the initial equation and the obtained one are equivalent. This means that both equations have the same solutions and thereby we can work with one or the other. We will use this property often in the elimination method.
Resolved Systems of Linear Equations
System 1
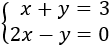
System 2
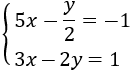
System 3
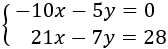
System 4
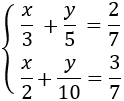

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.