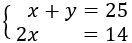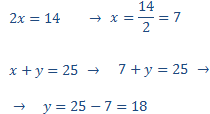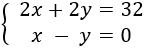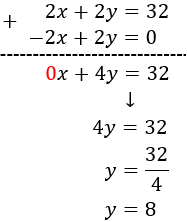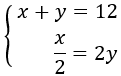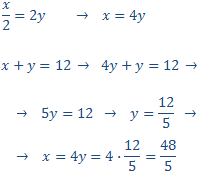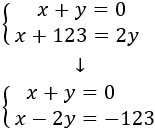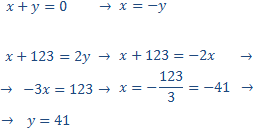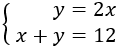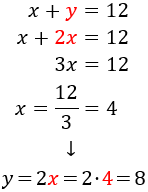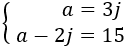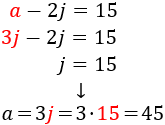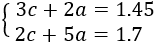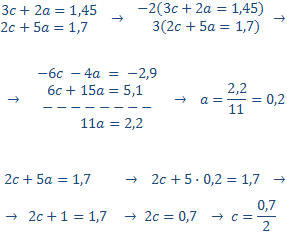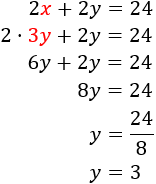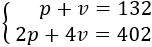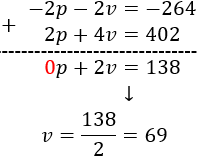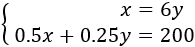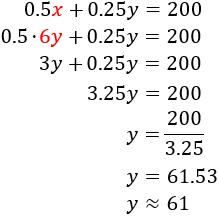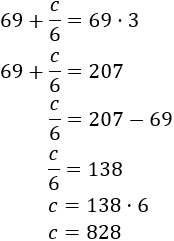We call x the first number and y the second number.

The numbers add 25:

$$ x + y = 25 $$

The double of one of the numbers is 14 (we can consider that this number is x):

$$ 2x = 14 $$

We have the system

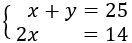
We apply substitution:

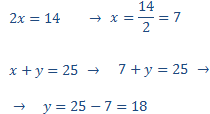
So, the numbers are 7 and 18.

We call x the first number and y the second number.

The double of the sum of two numbers is 32:

$$ 2(x + y) = 32 $$

The subtraction of them is 0:

$$ x - y = 0 $$

We have the system

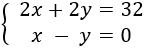
We apply reduction:

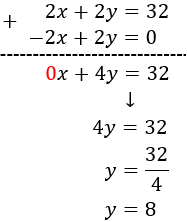
So, the numbers are 8 and 8.

x = first number

y = second number

The numbers add 12:

$$ x + y = 12 $$

Half of one of them is double the other:

$$ \frac{x}{2} = 2y $$

We have the system

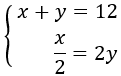
We apply substitution:

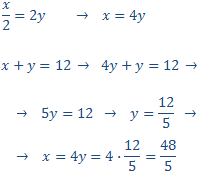
So, the numbers are

$$ \frac{18}{5},\ \frac{12}{5} $$

We call

x = first number

y = second number

The numebers add 0:

$$ x + y = 0 $$

If we add 123 to one of them, we get the double of the other one:

$$x + 123 = 2y $$

We have the system:

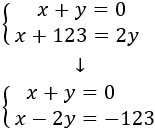
We apply substitution:

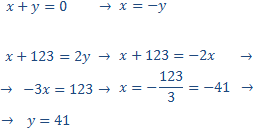
So, the numbers are 41 and -41.

The number is xy, where x is the first digit and y is the second one.

The second digit is double the first:

$$ y = 2x $$

Adding both digits gives 12:

$$ x + y = 12 $$

We have the system:

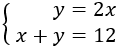
We resolve with substitution:

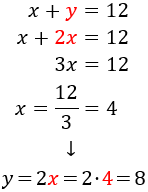
So, the number is 48.

We call

a =Anne's age

j = Jacob's age

Anne is three times the age of her son Jacob:

$$ a = 3j $$

In 15 years, Anne's age will be double Jacob's:

$$ ( a + 15 ) = 2( j + 15 ) $$

We have the system:

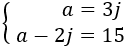
We apply substitution:

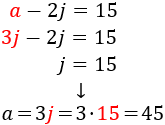
Anne is 45 years old and her son Jacob is 15 year's old, so Anne is 30 years older than her son.

We call

c = number of glass marbles

a = number of steel marbles

3 glass marbles and 2 steel ones are 1.45$:

$$ 3c + 2a = 1,45 $$

2 glass marbles and 5 steel ones are 1.7$:

$$ 2c + 5a = 1,7 $$

We have the system:

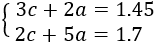
We apply reduction:

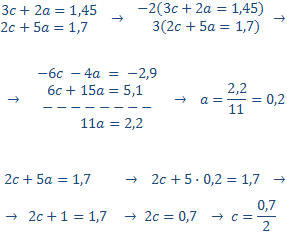
One steel marble is 0.2$ and a glass one is 0.35$.

The rectangle has 4 sides: two are the same as each other (base) and another two are the same as each other (height).

The perimeter is the sum of all the sides.

We call x the large side and y the short side.

The perimeter is 24:

$$ 2x + 2y = 24 $$

The large side measures three times the short side:

$$ x = 3y $$

We have the system:

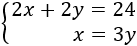
We apply substitution:

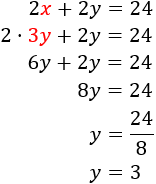
The large sides measure 9 units and the short sides 3 (each of them).

a. Take into account that each duck has 2 legs and each cow has 4. The sum is 402 (two legs per duck and 4 per cow).

p = number of ducks

v = number of cows

These animals add 132:

$$ p + v = 132 $$

The sum of their legs is 402 (two legs per duck and 4 per cow):

$$ 2p + 4v = 402 $$

We have the system:

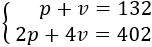
We apply reduction:

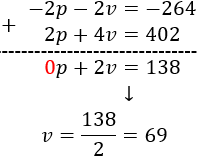
There are 63 ducks and 69 cows.

b. In accord with the quantities of food are estimated, we won't obtain a exact number of animals, only an estimation.

y = number of roosters

x = number of chickens

There is one rooster per 6 chickens:

$$x = 6y $$

A chicken eats is 0.5Kg, double what the rooster does. The total is 200Kg:

$$0,5x + 0,25y = 200 $$

We have the system:

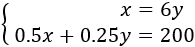
We apply substitution:

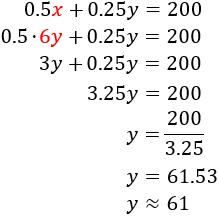
We can say there are 61 roosters and 366 chickens.

c. We know there are 69 cows.

c = number of rabbits

The sixth part of the rabbits are with the cows, so there are

$$ 69 + c/6 $$

animals in the cow's keep.

Counting the rabbits, the number of animals in the keep is triple:

$$ 69 + \frac{c}{6} = 69\cdot 3 $$

We resolve the linear equation:

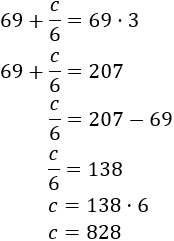
There are 828 rabbits.

We write the score as 100 instead of 10:

$$ 8.05 \cdot 10 = 80.5 $$

We call x the number of correct answers and y the wrong answers.

Due to the fact that all questions must be answered, the following equation must be true

$$ x + y = 100 $$

Each correct answer adds 1 and each wrong subtracts 0.5:

$$ 1\cdot x - 0.5 \cdot y = 80.5 $$

Now we resolve the equation system by substitution:

We isolate the x from the first equation:

$$ x + y = 100 $$

$$ x = 100 - y $$

Now we substitute x in the second equation:

$$ x - 0.5 \cdot y = 80.5 $$

$$ (100-y) - 0.5 \cdot y = 80.5 $$

We resolve the linear equation:

$$ 100-y - 0.5 \cdot y = 80.5 $$

$$ 100-80.5 = y +0.5 y $$

$$ 19.5 = 1.5y$$

$$ y = \frac{19.5}{1.5} = 13$$

We conclude that the amount of wrong answers is y = 13.

We can easily work out how may correct answers there are:

$$ x = 100 - y = 100 - 13 = 87 $$

We call the numerator x and the denominator y.

So, the fraction is

$$ \frac{x}{y} $$

We add 7 to the numerator and denominator and we get 2/3:

$$ \frac{x+7}{y+7} = \frac{2}{3} $$

Notice that from the equality above we get:

$$ 3(x+7) = 2(y+7) $$

We operate to simplify it:

$$ 3x+21 = 2y+14 $$

$$ 3x -2y = -7 $$

Now we proceed the same way but subtracting 3:

$$ \frac{x-3}{y-3} = \frac{1}{4} $$

We operate to simplify it:

$$ 4(x-3) = y-3 $$

$$ 4x-12 = y-3 $$

$$ 4x-y = 9 $$

Therefore the linear equation system is the following:

$$ 3x -2y = -7 $$

$$ 4x-y = 9 $$

We solve it with equalization (to change the method). Thus we isolate the x's from both equations.

From the first equation:

$$ 3x -2y = -7 $$

$$ x = \frac{-7+2y}{3} $$

From the second equation:

$$ 4x-y = 9 $$

$$ x = \frac{9+y}{4} $$

We equal both x's:

$$ \frac{-7+2y}{3} = \frac{9+y}{4}$$

We resolve the linear equation:

$$ 4(-7+2y) = 3(9+y)$$

$$ -28+8y = 27 + 3y $$

$$ 5y = 55 $$

$$ y = \frac{55}{5} = 11 $$

We calculate x from y:

$$ x = \frac{-7+2y}{3} =$$

$$ x = \frac{-7+22}{3} =$$

$$ x = \frac{15}{3} =$$

$$ x = 5 $$

So, the fraction we obtain is

$$ \frac{x}{y} = \frac{5}{11} $$

The 1230 2L bottles are equivalent to a total of

$$ 1230 \cdot 2 = 2460 L $$

litres of lemonade.

One of the equations of the system is the one provided by the exercise information.

The other equation is the following:

$$ L_L + L_A = 2460 $$

So, the total litres of lemonade is the sum of water and concentrate.

We resolve the system by substitution:

From the second equation:

$$ L_L = 2460 - L_A $$

We substitute in the first equation:

$$ L_L = \frac{2 L_A}{5} $$

$$ 2460 - L_A = \frac{2 L_A}{5} $$

We resolve the linear equation:

$$ 5\cdot 2460 - 5L_A = 2L_A $$

$$ 12300 = 5L_A + 2L_A $$

$$ 12300 = 7L_A $$

$$ L_A = \frac{12300}{7} = 1757.14L $$

Note: L indicates the litres, it has nothing to do with the name of the unknown factor.

Now we calculate the litres of lemon concentrate:

$$ L_L = 2460 - 1757.14 = 702.86L $$

Since we need 20 lemons to make a litre of concentrate and we want 702.86L of concentrate, we need

$$ 20\cdot 702.86 = 14057.2 $$

The total of lemons needed is 14058.

We call b the base of the rectangle and a the height.

Note that the length of the rope is the perimeter. Therefore

$$ 2a + 2b = 34 $$

If we draw the diagonal of the rectangle, we will see two right angle triangles, the hypotenuse being the diagonal:

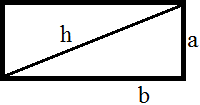
We apply the Pithagoras' Theorem:

$$ a^2 + b^2 = h^2 $$

where h represents the hypotenuse (the diagonal). Then,

$$ a^2 + b^2 = 13^2 = 169 $$

The difficulty of the problem is due to the fact the last equation is not linear (the unknown factors are to the power of two).

We isolate a from the first equation:

$$ 2a + 2b = 34 $$

$$ a = \frac{34-2b}{2} = 17-b$$

Now we substitute a in the non lineal equation:

$$ a^2 + b^2 = 169 $$

$$ (17-b)^2 + b^2 = 169 $$

We calculate the square of the subtraction (newton's binomial theorem):

$$ (17-b)^2 = 17^2 +b^2 -2\cdot 17b =$$

$$ = 289 +b^2 -34b $$

Then, we have a quadratic equation:

$$ 289 +b^2 -34b + b^2 = 169 $$

We simplify a bit:

$$ 2b^2 -34b +120 =0 $$

We omit the procedure, because it does not belong to the unit of systems of equations.

The solutions are:

$$ b=12,\ b=5 $$

So a has two values:

$$ a = 17-b = 17-5=12 $$

$$ a = 17-b = 17-12=5 $$

Notice that in fact there is only one solution to the problem, because if we consider b = 12 then a = 5 and if b = 12, then a = 5. This is due to the fact is does not matter if we consider a side as the base or the height.

Therefore the sides of the rectangle are 12 and 5 meters.

We will call the number of VIP tickets v and the number of normal tickets n (it does not matter what name we give the unknown factors).

The total number of tickets is the same as the number of people:

$$ v + n = 160 $$

They raise:

$$ 300v + 50n = 23000 $$

We resolve the system with equalization. Thus we isolate c in both equations:

From the first equation:

$$ v = 160-n $$

From the second equation:

$$ v = \frac{23000 - 50n}{300} $$

We equal both expressions:

$$ 160-n = \frac{23000 - 50n}{300} $$

The solution to the linear equation above is:

$$ n = 100 $$

Therefore

$$ v = 160-100 = 60 $$

So, they sold 60 VIP tickets and 100 normal.

We will call g the number of green balls, r the number of red balls and y the number of yellow balls.

The second point says that

$$ g+r = 5y $$

The third point says that

$$ g = 3y $$

And the fourth point says that

$$ y+r = 123 $$

We have a system of linear equations of 3 equations with 3 unknown factors.

We apply substitution:

We substitute g from the second equation in the first one:

$$ g+r = 5y $$

$$ 3y+r = 5y $$

We isolate r:

$$ r = 5a -3a $$

$$ r = 2a $$

We substitute r in the third equation:

$$ y+r = 123 $$

$$ y+2y = 123 $$

$$ 3y = 123 $$

$$ y = 41 $$

Now we use the value of y to obtain the other unknown factors:

$$ r = 2y = 82 $$

$$ g = 3y = 123 $$

Since the numbers are 3 digits long, it will look like

$$ xy0 $$

or

$$ x0y $$

where x and y represents digits.

Notice that the numbers 0xy are not really three digit long, because 0xy = xy.

In both cases, it has to be

$$ x+y = 7 $$

Hence we have these possibilities

x	y	x + y
1	6	7
2	5	7
3	4	7
4	3	7
5	2	7
6	1	7
7	0	7

Notice that x cannot be 0, because in both cases it is the first digit.

In the table we have the 7 possibilities and are valid for both cases.

So, to start with there will be 14 numbers, but we have to remove one because the values of the last row provide the same number.

The solution is 13 numbers.