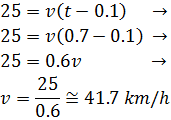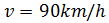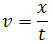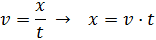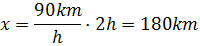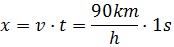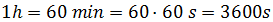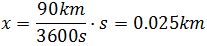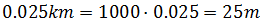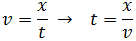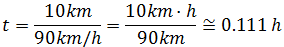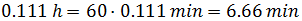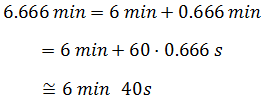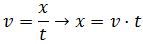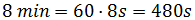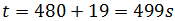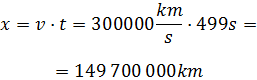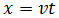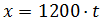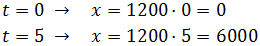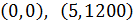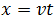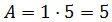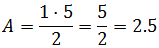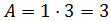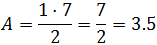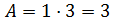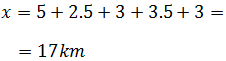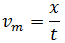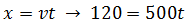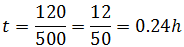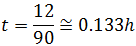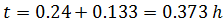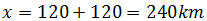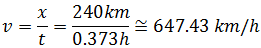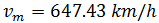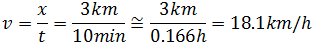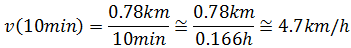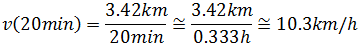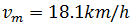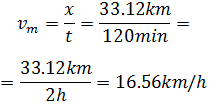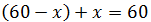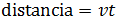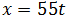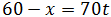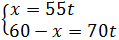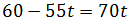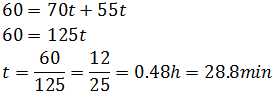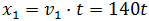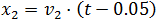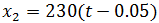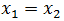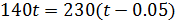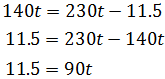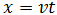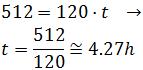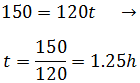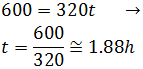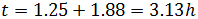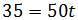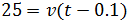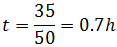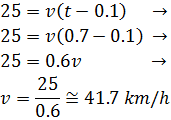Problema 1
Un camión se mueve a velocidad constante de 90km/h por una autopista recta.
- ¿qué distancia recorre en 2 horas?
- ¿qué distancia recorre por segundo?
- ¿cuánto tardará en recorrer 10km?
SOLUCIÓN:
La velocidad del camión es
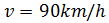
expresada en kilómetros (espacio) por hora (tiempo).
Apartado a: ¿qué distancia recorre en 2 horas?
La ecuación del movimiento es
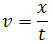
donde conocemos la velocidad y el tiempo.
Queremos obtener la distancia recorrida: aislamos la
x antes de sustituir en la ecuación:
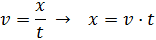
Ahora sustituimos los datos
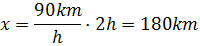
Hemos escrito las unidades de tiempo para tratarlas como factores,
de este modo, como el tiempo, h, está multiplicando y dividiendo, desaparece,
quedando únicamente la unidad de distancia, km.
Por tanto, el camión recorre 180 kilómetros en 2 horas.
Apartado b: ¿qué distancia recorre por segundo?
De nuevo tenemos que calcular la distancia, pero ahora, en un tiempo de 1 segundo.
Sabemos que la distancia recorrida es
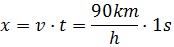
Notemos que en el denominador tenemos el tiempo en horas y en el numerador en
segundos. Necesitamos la misma unidad. Para ello, pasaremos las horas a segundos.
Una hora son
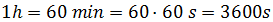
Entonces, escribimos 3600s donde tenemos la h:
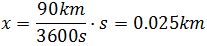
Como las unidades del tiempo son la misma, se han anulado.
El espacio recorrido obtenido está en kilómetros, por lo que si queremos evitar
los decimales podemos pasarlo a metros:
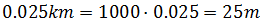
Por tanto, el camión recorre 25 metros cada segundo.
Apartado c: ¿cuánto tardará en recorrer 10km?
Ahora sabemos la distancia, x = 10km , y tenemos que calcular el tiempo.
Aislamos el tiempo en la ecuación:
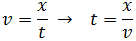
y sustituimos los datos
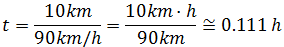
Notemos que las horas están dividiendo en el denominador, por lo que pasan
multiplicando al numerador.
Escribimos el tiempo en minutos para evitar los decimales:
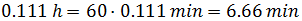
Para ser más exactos,
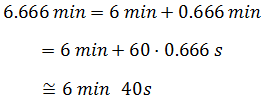
Por tanto, el camión tarda unos 6 minutos y 40 segundos en recorrer 10km.
Problema 2
La velocidad de la luz en el vacío es
c = 300 000 km/s. La luz del Sol tarda en llegar a la
Tierra 8 minutos y 19 segundos. Calcular la distancia entre el Sol y la Tierra.
SOLUCIÓN:
La velocidad la hemos llamado c en vez de v ya que para la luz se
utiliza este nombre, pero el procedimiento es el mismo.
Por tanto, conocemos la velocidad, c, y el tiempo, t = 8 min 19s.
Podemos calcular la distancia:
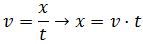
Antes de sustituir tenemos que expresar el tiempo en una sola unidad.
Como la velocidad la tenemos en kilómetros por segundo,
pasamos el tiempo a segundos:
Por un lado, los 8 minutos son
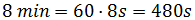
Por tanto, el tiempo es
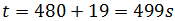
Ahora sustituimos los datos en la ecuación:
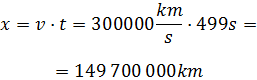
Por tanto, la distancia del Sol a la Tierra es de 149 700 000km, es decir,
casi 150 millones de kilómetros.
Problema 3
Dibujar la gráfica del espacio recorrido en función del tiempo y la
gráfica de la velocidad en función del tiempo del movimiento
rectilíneo uniforme de una aeronave que vuela a 1200 km/h.
SOLUCIÓN:
La ecuación del movimiento rectilíneo uniforme es
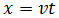
Sustituimos la velocidad y obtenemos
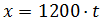
Como la velocidad está en kilómetros por hora, la unidad de medida del
tiempo, t, será horas y la del espacio, x, en kilómetros.
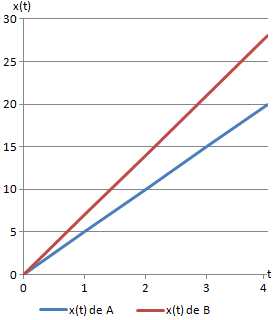
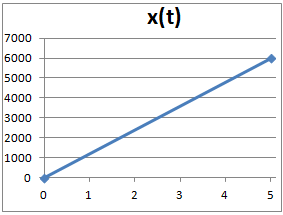
Para dibujar la gráfica del espacio recorrido en función del tiempo,
damos dos valores a t y dibujamos el par (x,t).
Escogemos, por ejemplo,
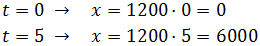
Una vez dibujados los puntos
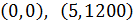
Sólo tenemos que unirlos en línea recta ya que sabemos que en este tipo
de movimiento el espacio es una recta con pendiente
la velocidad (la ecuación es una ecuación lineal):
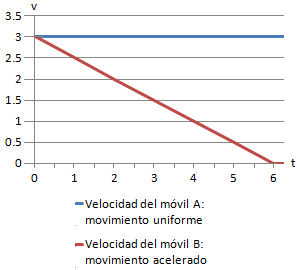
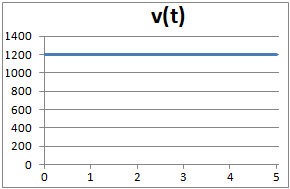
Como la velocidad es constante,
la gráfica de v(t) será una recta horizontal, una recta paralela al eje
de abscisas:
Problema 4
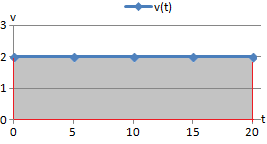
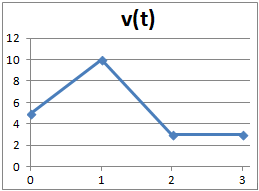
La siguiente gráfica representa la velocidad (km/h)
en función del tiempo de un automóvil.
Calcular la distancia que recorre el automóvil sin hacer
uso de las ecuaciones del movimiento ya que se trata de un
movimiento con velocidad no constante.
SOLUCIÓN:
Sabemos que el espacio recorrido es
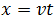
y que, por tanto, el área que se encuentra por debajo de la gráfica
de la velocidad en función del tiempo es el espacio recorrido.
Para calcular el área tenemos que dividirla en tres polígonos:
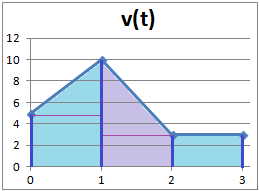
El primer polígono lo dividimos en un rectángulo y un triángulo:
El área del rectángulo es
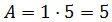
El área del triángulo es
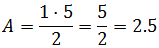
Procedemos de igual modo con el segundo polígono:
El área del rectángulo es:
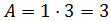
Y la del triángulo es
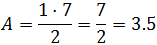
El último polígono es un rectángulo de base 1 y altura 3. Su área es
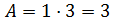
Ahora sumamos todas las áreas y tendremos la distancia recorrida:
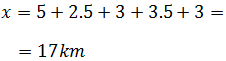
Por tanto, el espacio recorrido son 17 km. Sabemos que
son kilómetros porque en la gráfica el tiempo está en horas y la velocidad en
kilómetros por hora.
Problema 5
En un movimiento rectilíneo con velocidad no constante, la velocidad media es
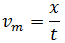
donde x es la distancia recorrida final y t el tiempo transcurrido.
La velocidad media es la velocidad que el móvil debería tener para recorrer
la misma distancia en el mismo tiempo realizando un movimiento rectilíneo uniforme,
es decir, con velocidad constante.
Sabemos que un cohete espacial recorre 120km a una velocidad constante de 500km/h.
Cuando alcanza los 120km, su velocidad pasa a ser, de forma instantánea,
900km/h. A esta velocidad recorre otros 120km.
Calcular la velocidad media del cohete.
SOLUCIÓN:
En realidad, se trata de dos movimientos rectilíneos uniformes: uno durante
los primeros 120 kilómetros y el otro durante los 120 kilómetros restantes.
En cada uno de estos dos movimientos tenemos una velocidad distinta y,
por tanto, como la distancia es la misma, cada movimiento tendrá una duración.
En el primer movimiento, la velocidad es de 500km/h. Por tanto, tenemos la ecuación
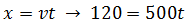
El tiempo que dura el movimiento es de
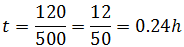
En el segundo, la velocidad es de 900km/h.
Del mismo modo que antes, obtenemos que el tiempo es
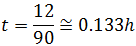
Por tanto, el tiempo total transcurrido es
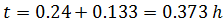
Y la distancia total recorrida es
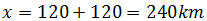
Ahora supongamos que realizamos un movimiento rectilíneo uniforme durante
0.373 horas y recorremos una distancia de 240 kilómetros. La velocidad de este
movimiento es:
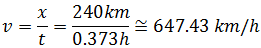
Por tanto, la velocidad media del cohete es
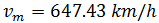
Problema 6
Las siguientes tablas recogen los tiempos y las distancias
recorridas por dos ciclistas que parten en el mismo instante
desde el mismo origen y en el mismo sentido en línea recta:
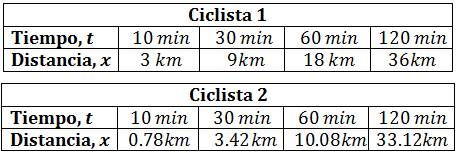
Dibujar las gráficas que corresponden a los datos para
responder a las siguientes preguntas:
- ¿las velocidades son constantes o los movimientos son acelerados?
- calcular la velocidad media de cada ciclista.
- ¿qué ciclista habrá recorrido una distancia mayor transcurridas 3 horas
desde el instante de la salida?
SOLUCIÓN:
Apartado a:
Sabemos que en el movimiento rectilíneo uniforme la gráfica de la
distancia recorrida en función del tiempo tiene que ser una recta.
Por tanto, la velocidad del ciclista 2 no puede ser constante.
Podemos comprobar que la velocidad del ciclista 1 es constante
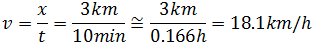
Y obtenemos esta velocidad para cualquier para de datos de la tabla que tomemos.
En cambio, para el ciclista 2 tenemos que, para el tiempo t = 10 min, la velocidad es
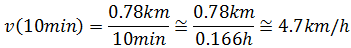
Mientras que para el tiempo t = 20 min la velocidad es
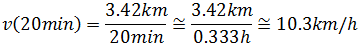
Y cada vez obtenemos una velocidad mayor. La velocidad no
es constante, es un movimiento acelerado.
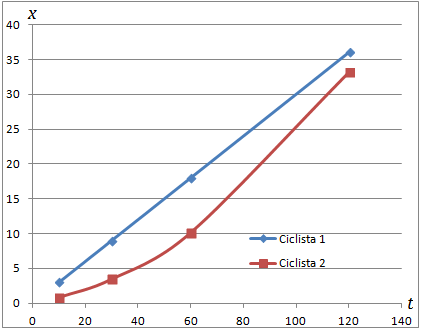
Apartado b:
La velocidad media es la velocidad que debería tener el móvil
para recorrer la misma distancia en el mismo tiempo con velocidad constante.
Como la velocidad del ciclista 1 es constante, su velocidad media es
dicha velocidad, es decir,
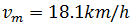
La velocidad del ciclista 2 no es constante.
Su velocidad media es la distancia recorrida entre el tiempo
empleado, esto es,
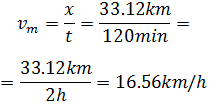
Apartado c
Puesto que no sabemos exactamente cómo es el
movimiento del ciclista 2, no podemos estar seguro de
quién recorrerá más distancia. Pero a partir de los 80 minutos,
la gráfica del ciclista 2 crece más rápidamente que
la del ciclista 1.
Si suponemos que las gráficas siguen
con el mismo crecimiento, transcurridas las 3 horas,
la gráfica del ciclista 2 crecerá por encima de la otra gráfica
y, por tanto, la distancia recorrida será mayor.
Problema 7
En el mismo instante, una motocicleta sale de la ciudad A y otra de la ciudad B,
con la intención de encontrarse en el camino recto de 60 kilómetros que une
ambas ciudades.
Sabiendo que las velocidades de las motocicletas son 70km/h y 55km/h,
calcular cuánto tardarán en encontrarse.
SOLUCIÓN:
El diagrama de la situación es
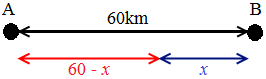
Como cada motocicleta circula a una velocidad,
no se encuentran en la mitad del camino. La que tiene
una velocidad menor habrá recorrido x kilómetros y,
por tanto, la otra habrá recorrido 60-x, ya que la suma de
ambas distancias ha de ser la distancia que hay entre
las ciudades. En efecto,
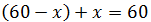
Por otro lado, el tiempo es el mismo para ambas motocicletas
ya que salen en el mismo instante.
La ecuación del movimiento rectilíneo uniforme es
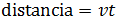
Para la motocicleta que circula a 55km/h tenemos
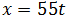
Y, para la otra
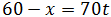
Tenemos un sistema de ecuaciones:
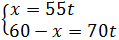
Sustituimos la primera ecuación en la segunda:
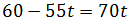
Resolvemos la ecuación de primer grado:
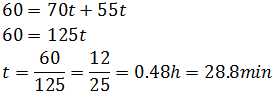
Por tanto, las motocicletas se encuentran transcurridos unos
29 minutos desde su salida.
Problema 8
En una persecución policial, el automóvil a la fuga lleva una velocidad de
140km/h cuando pasa por un determinado punto de una carretera.
Tres minutos después, el automóvil oficial que sigue al anterior
pasa por dicho punto a una velocidad de tan solo 230km/h para evitar
causar un accidente con los demás vehículos de la carretera a causa de
un exceso de velocidad.
Se supone que las velocidades indicadas son constantes y la
carretera es recta. Calcular cuánto tardará la policía en alcanzar al
delincuente.
SOLUCIÓN:
Puesto que las velocidades son en kilómetros por hora,
para el tiempo usaremos horas. Tres minutos son 3/60 h = 0.05 h .
El determinado punto de la carretera es el punto de referencia que usaremos.
Este punto será x = 0.
El punto donde se encuentran, que no sabemos cuál es, lo llamaremos z.
Usaremos la siguiente notación:
x1, v1 son el espacio recorrido y la velocidad,
respectivamente, del automóvil a la fuga.
x2, v2 son el espacio recorrido y la velocidad,
respectivamente, del automóvil policial
Por tanto, tenemos que
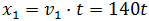
Sin embargo, la ecuación para la policía es
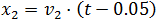
Ya que la policía comienza el movimiento 0.05 horas después
(consideramos que el movimiento comienza cuando el vehículo pasa
por el punto x = 0).
Por tanto,
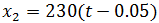
La policía alcanzará al delincuente cuando ambos automóviles
hayan recorrido la misma distancia, dicho matemáticamente, cuando
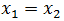
Esto ocurrirá en el punto que hemos llamado anteriormente z.
La igualdad x1 = x2 es la misma que
(sustituyendo las ecuaciones)
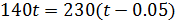
Tenemos una ecuación de primer grado. La resolvemos:
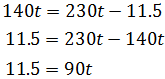
Despejamos el tiempo
$$ t = \frac{11.5}{90} \simeq 0.13 h$$
$$ 0.13h · 60 = 7.8 min $$
Por tanto, la policía tardará aproximadamente 8 minutos en alcanzar al delincuente.
Problema 9
Las ciudades A y B distan 600 kilómetros. Hay un tren de alta
velocidad que circula entre ambas ciudades a 320km/h.
En otra ciudad, C, a 150 kilómetros en línea recta de la
ciudad A y a 512 kilómetros en línea recta de la ciudad B,
un motorista tiene que decidir qué ruta tomar para llegar a la ciudad B.
Las posibilidades son las siguientes:
- viajar desde C hasta B en su motocicleta
- viajar desde C hasta A en su motocicleta y desde A hasta B en tren
Encontrar la ruta más rápida sabiendo que la velocidad a la que circula
la motocicleta es 120km/h. ¿Es la ruta más corta en cuanto a distancia?
SOLUCIÓN:
La situación de las ciudades es la siguiente
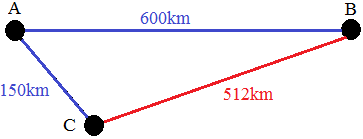
Los movimientos son rectilíneos uniformes,
por lo que usaremos la ecuación
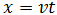
Calculamos el tiempo que requiere la primera ruta:
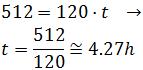
La otra ruta la tenemos que descomponer en
dos movimientos (rectilíneos uniformes):
Por tanto, la ruta más rápida es la segunda, es decir, de C a A y de A a B.
Sin embargo, es la ruta más larga puesto que se recorren 750km.
Problema 10
Dos caminos rectos, A y B, terminan en el mismo punto,
que es el punto de encuentro de dos amigos: Félix y Erika.
La longitud del camino A y B es 25km y 35km, respectivamente.
Félix circula por el camino B a una velocidad de 50km/h y Erika
circula por el camino A. Calcular la velocidad a la que tiene que
viajar Erika para que ambos amigos lleguen al punto de encuentro
en el mismo instante sabiendo que Erika comenzó su viaje 6 minutos
más tarde que Félix.
SOLUCIÓN:
El movimiento de cada amigo es rectilíneo y uniforme.
Para Félix tenemos la ecuación:
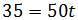
Como Erika parte 6 minutos más tarde, su tiempo lleva un retraso de
6 minutos, su ecuación es
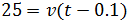
Ya que 6 minutos son 0.1h
Tenemos un sistema de dos ecuaciones y dos incógnitas.
De la primera ecuación obtenemos el tiempo, t:
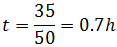
Sustituimos en la segunda ecuación para obtener la velocidad: