Contenido de esta página:
Recordatorio del MRU
MRUA: definición, fórmulas y gráficas
11 problemas resueltos de MRUA
Nota: en este tema, se considera el movimiento en 1 dimensión, por lo que no se utilizan vectores.
Definición, ecuación y gráficas.
Definición, fórmulas y gráficas.

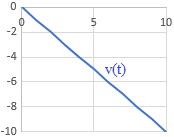
Describir el movimiento de la siguiente gráfica de un móvil que se mueve en línea recta y calcular \(v(0)\), \(v(4)\), \(v(10)\) y \(v(15)\):
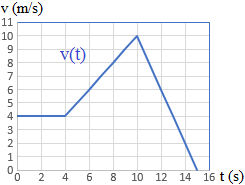
¿La gráfica podría corresponder a un móvil que se mueve en círculos y no en línea recta?
Es la gráfica de la velocidad en función del tiempo de un movimiento.
Observando la gráfica podemos deducir:
Además, observando la gráfica, las velocidades son
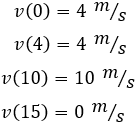
Es decir, el móvil se encuentra inicialmente en movimiento con velocidad constante, posteriormente aumenta su velocidad hasta el instante t = 10s, cuando comienza a decrecer su velocidad hasta quedar inmóvil en el instante t = 15s.
La gráfica nos informa sobre la velocidad del móvil en función del tiempo, independientemente de la forma de su trayectoría. Un móvil sí podría moverse en círculos con esta gráfica de v/t.

Elegir la gráfica de la velocidad en función del tiempo que se corresponde a cada situación.
Gráfica a:
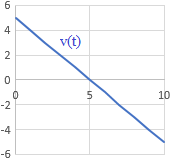
Gráfica b:
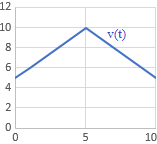
Gráfica c:
Situaciones:
Dejar caer una moneda desde la azotea de un edificio: el movimiento comienza en el momento en el que se suelta la moneda y termina cuando ésta llega al suelo.
Lanzar una moneda hacia arriba en línea recta: el movimiento comienza cuando se suelta la moneda y termina cuando cae al suelo.
Efectuar un adelantamiento a un auto en marcha con otro auto: el movimiento comienza justo antes de realizar el adelantamiento y termina cuando, una vez rebasado el auto, se lleva la misma marcha que al inicio.
La gráfica a describe la situación 2. En el instante \(t=0\) la velocidad no es 0 porque la moneda tiene una velocidad inicial positiva necesaria para moverse hacia arriba. La velocidad decrece hasta llegar a 0 por el efecto de la gravedad (cuando la moneda alcanza la altura máxima). En dicho instante, el efecto de la gravedad provoca que la velocidad siga decreciendo y volverse negativa, lo que se corresponde con el movimiento de la caída libre de la moneda.
La gráfica b describe la situación 3. En \(t=0\) el auto no tiene velocidad 0 porque está en marcha. La velocidad aumenta hasta rebasar al otro auto y después, decrece para continuar con su marcha.
La gráfica c describe la situación 1. La velocidad en \(t=0\) es 0 puesto que la moneda está inicialmente en reposo. La velocidad decrece por efecto de gravedad.

Calcular la aceleración (en \(m/s^2\)) que se aplica para que un móvil que se desplaza en línea recta a 90.0 km/h reduzca su velocidad a 50.0 km/h en 25 segundos.
Comentar el resultado.
La velocidad inicial del móvil es
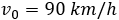
También conocemos la velocidad a los 25 segundos:
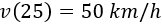
La fórmula de la velocidad es
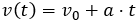
Despejamos la aceleración:
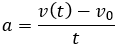
Antes de sustituir los datos, escribimos la velocidad en metros por segundo para tener las mismas unidades:

Sustituimos los datos en la fórmula de la aceleración que obtuvimos anteriormente:
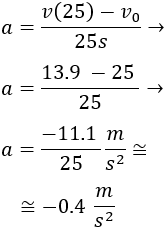
Por tanto, la aceleración es de \(-0.4 m/s^2\).
Como la velocidad inicial es positiva y el móvil va frenándose, entonces la aceleración es negativa.

Un tren de alta velocidad en reposo comienza su trayecto en línea recta con una aceleración constante de \(a = 0.5m/s^2\). Calcular la velocidad (en kilómetros por hora) que alcanza el tren a los 3 minutos.
Como el tren está en reposo, la velocidad inicial es 0:
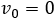
Nótese que la aceleración es en metros por segundos al cuadrado y el tiempo es en minutos. Debemos escribir el tiempo en segundos:
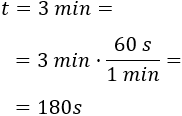
Calculamos la velocidad aplicando la fórmula:
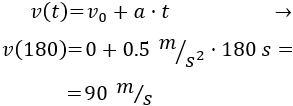
Tenemos la velocidad en metros por segundo, así que la escribimos en kilómetros por hora:
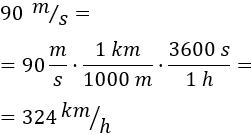
Por tanto, la velocidad del tren a los tres minutos es \(324km/h\).

Calcular la aceleración que aplica un tren que circula por una vía recta a una velocidad de 216.00km/h si tarda 4 minutos en detenerse desde que acciona el freno.
La velocidad inicial del tren es
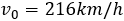
La escribimos en metros por segundo:
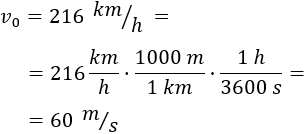
Escribimos el tiempo en segundos:
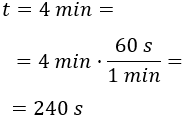
La velocidad final, es decir, a los 4 minutos, es 0 puesto que debe detenerse:
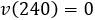
Despejamos la aceleración de la fórmula de la velocidad:
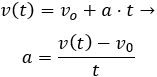
Sustituimos los datos:
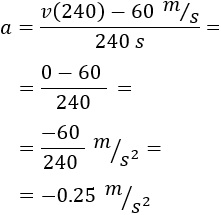
Por tanto, la aceleración es \(-0.25 m/s^2\).

Un ciclista que está en reposo comienza a pedalear hasta alcanzar los 16.6km/h en 6 minutos. Calcular la distancia total que recorre si continúa acelerando durante 18 minutos más.
Como el pedaleo continúa durante 18 minutos, el movimiento dura un total de 24 minutos.
Primero, calculamos la aceleración sabiendo que en 6 minutos pasa del reposo a 16.6km/h. Los 6 minutos son \(6/60 =0.1\) horas.
Despejamos la aceleración de la fórmula de la velocidad:
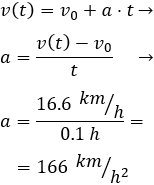
Ahora, calculamos la posición a los 24 minutos (son \(24/60 = 0.4\) horas):
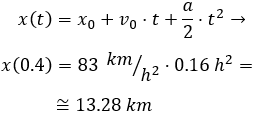
El ciclista recorre 13.28 kilómetros.

En una carrera cuyo recorrido es recto, una moto circula durante 30 segundos hasta alcanzar una velocidad de 162.00km/h. Si la aceleración sigue siendo la misma, ¿cuánto tiempo tardará en recorrer los 200 metros que faltan para rebasar la meta y a qué velocidad lo hará?
Debemos considerar el movimiento desde que comienza la carrera. Suponemos que la moto se encuentra en reposo al inicio:
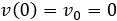
Cuando la moto está en la salida, la posición inicial es 0:
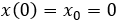
La moto aplica una aceleración (constante) y la velocidad aumenta hasta 162.00km/h en 30 segundos.
Escribimos la velocidad en metros por segundo:
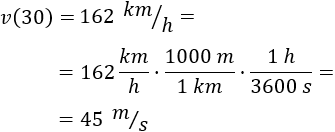
Calculamos la aceleración:
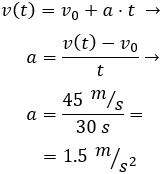
Calculamos la posición a los 30 segundos:
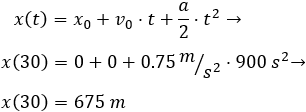
La moto debe recorrer en total 875 metros. Podemos calcular el tiempo sabiendo la distancia total:
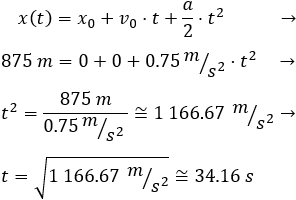
Por tanto, el tiempo que tardará en recorrer los últimos 200 metros es 4.16 segundos y la velocidad será
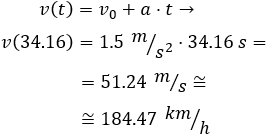

Dejamos caer una moneda desde una altura de 122.5 metros. Calcular el tiempo que tarda en posarse sobre el suelo.
Nota: la gravedad es \(g=9.8m/s^2\).
La velocidad inicial de la moneda es 0:
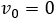
Cuando la soltamos, la velocidad aumenta por efecto de la gravedad hasta llegar al suelo. Luego la aceleración es
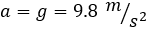
La velocidad en el instante \(t\) es
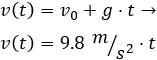
Para calcular el tiempo, aplicamos la fórmula de la posición:
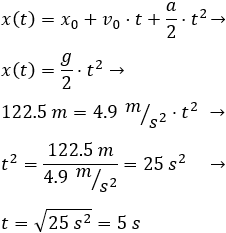
Por tanto, la moneda tarda 5 segundos en llegar al suelo.

Desde 600 metros de altura se lanza hacia el suelo una botella de cristal con una velocidad inicial de \(18.36km/h\). Calcular la velocidad de la botella en el instante previo de romperse contra el suelo.
La velocidad inicial de la botella es
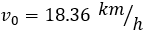
La escribimos en metros por segundo:
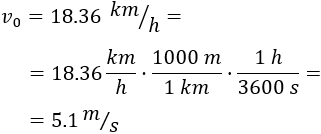
La aceleración es la gravedad:
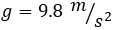
Nota: hemos escrito la velocidad inicial de la botella con signo positivo. Por tanto, como la botella se dirige hacia el suelo, la gravedad debe tener el mismo signo. Si el lanzamiento fuera hacia el cielo, la gravedad tendría que ser negativa.
La velocidad en el instante \(t\) es
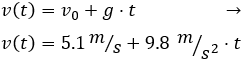
Para calcular el tiempo, aplicamos la fórmula de la distancia recorrida:
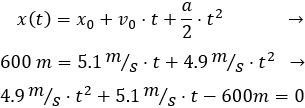
Resolvemos la ecuación de segundo grado:
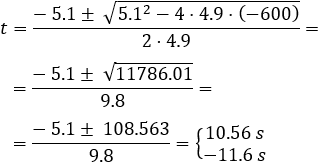
La solución es \(t=10.56s\) ya que el tiempo no puede ser negativo.
Calculamos la velocidad en \(t=10.56s\):
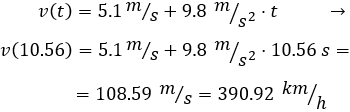

Un estudiante de física dispara una pistola lanza-pelotas en línea recta desde el suelo. Según las especificaciones de la pistola, la velocidad de lanzamiento es de \(29.4 m/s\).
Calcular la altura que alcanza la pelota y el tiempo que tarda en caer al suelo desde que se dispara.
La pelota comienza un movimiento vertical hacia arriba con una velocidad inicial
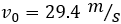
Como el movimiento es hacia arriba y el efecto de la gravedad es contrario, debemos escribir una aceleración negativa:
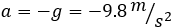
En un determinado tiempo, \(t_1\), la pelota tendrá velocidad 0. Es el momento en el que se detiene para comenzar a caer.
Primero, estudiamos el movimiento hasta \(t_1\).
La velocidad en el instante \(t_1\) de la pelota es 0:
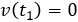
Podemos calcular \(t_1\) a partir de la fórmula de la velocidad:
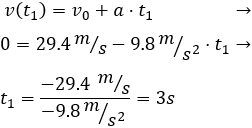
Calculamos la altura que alcanza la pelota:
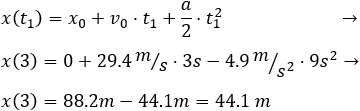
Por tanto, la altura que alcanza la pelota es 44.1 metros y el tiempo que tarda es 3 segundos.
Ahora, consideramos otro movimiento. Éste consiste en una caída libre de 44.1 metros: la velocidad inicial es 0 y la gravedad es \(-9.8m/s^2\).
La velocidad en el instante \(t_2\) es
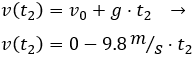
Para calcular el tiempo que tarda en caer, utilizamos la fórmula de la posición sabiendo que tiene que recorrer 44.1 metros:
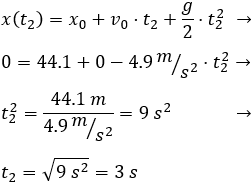
Por tanto, la pelota tarda 6 segundos en caer al suelo (desde que se dispara) y la altura máxima que alcanza es de 44.1 metros.
Nota: cuando la pelota ya está en el suelo tiene velocidad 0, pero no podemos utilizar este dato para calcular el tiempo que tarda en caer ya que esta velocidad no es debido al efecto de la gravedad, sino al del suelo. Por tanto, hemos considerado la velocidad en el instante en el que la pelota va a tocar el suelo.
Es interesante comentar que el objeto tarda lo mismo en subir que en bajar. Esto se debe a que la gravedad es constante.
Asimismo, la velocidad inicial del objeto (en valor absoluto) coincide con la velocidad final (justo antes de impactar en el suelo):
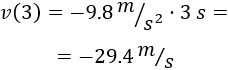
La velocidad inicial y la final tienen signos distintos ya que tienen sentidos opuestos: sentido de subida y sentido de bajada.

En un movimiento rectilíneo uniformemente acelerado, se define la velocidad media como
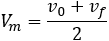
siendo \(v_0\) la velocidad inicial y \(v_f\) la velocidad final.
El teorema de la velocidad media de Merton establece que la distancia que recorre un móvil en un MRUA es la misma que la que recorre un móvil en un MRU con velocidad constante e igual a la velocidad media del primero.
Obtener la fórmula de la distancia que recorre un móvil (longitud de la trayectoria) en un MRUA aplicando el teorema de Merton y sabiendo que la velocidad en un MRUA es
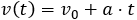
La distancia recorrida en un MRU es
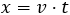
Aplicamos el teorema sustituyendo la velocidad en la fórmula anterior del MRU por la velocidad media del MRUA:
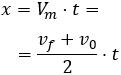
Podemos escribir la velocidad media en función del tiempo que dura el movimiento:
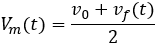
Así, la distancia recorrida es
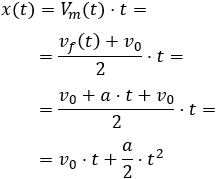
Movimiento Rectilíneo Uniformemente Acelerado (MRUA) - (c) - matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.