Dimensión de semejanza y de Hausdorffde fractales autosemejantes |
Contenido de esta página:
-
Introducción: dimensión de semejanza y de Hausdorff.
-
Dimensión de semejanza o de homotecia.
-
Ejemplos: cálculo de la dimensión de Hausdorff de fractales producidos por un IFS.
Los IFS de la mayoría de los fractales que aparecen en esta página se encontran en la página: Construccuión de fractales autosemejantes.
1. Introducción
Vamos a definir y a calcular la dimensión de semejanza de fractales autosemejantes. Cada uno de estos fractales es el atractor de algún sistema de funciones iteradas (IFS).
En el caso de este tipo de fractales, las dimensiones de semejanza y la de Hausdorff-Besicovitch (definición mucho más compleja) coinciden. Más concretamente, estas dimensiones son la solución de la ecuación
$$ r_1^{D}+r_2^{D}+..+r_n^{D} = 1$$
donde ri es la razón de cada función fi contractiva del IFS.
En los ejemplos que veremos en esta página todas las funciones que conforman los IFS tienen la misma razón de contracción r, por lo que el fractal está formado por n copias de sí mismo a escala r. Por tanto, tendremos
$$ nr^D = 1 $$
$$ r^D = \frac{1}{n}$$
$$ D\cdot ln(r) = -ln(n) $$
$$ D = -\frac{ln(n)}{ln(r)} = \frac{ln(n)}{ln\left(\frac{1}{r}\right)} $$
2. Dimensión de semejanza
Se define la dimensión de semejanza o de homotecia de un fractal autosemejante formado por n copias de sí mismo a escala r como
$$D = \frac{ln(n)}{ln(\frac{1}{r})}$$
Esta definición nos proporciona resultados como:
la dimensión de un segmento es 1:
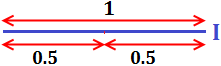
El segmento de longitud 1, I = [0,1], es un fractal autosemejante formado por 2 copias suyas a escala r = 0.5.
Luego su dimensión de semejanza es
$$D = \frac{ln(2)}{ln(2)} = 1$$
la dimensión de un cuadrado es 2:

El cuadrado de lado 1, I2 = [0,1]2, es un fractal autosemejante formado por 4 copias suyas a escala r = 0.5.
Luego su dimensión de semejanza es
$$D = \frac{ln(4)}{ln(2)} = 2$$
la dimensión de un cubo es 3:
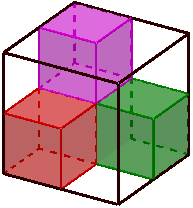
El cubo de lado 1, I3 = [0,1]3, es un fractal autosemejante formado por 8 copias suyas a escala r = 0.5.
Luego su dimensión de semejanza es
$$D = \frac{ln(8)}{ln(2)} = 3$$
3. Ejemplos
En este apartado calculamos la dimensión de Hausdorff de fractales generados por un sistema de funciones iteradas (IFS). Como dijimos en la introducción, en este tipo de fractales la dimensión de Hausdorff coincide con la dimensión de semejanza, así que calcularemos directamente la dimensión de semejanza.
Triángulo de Sierpinski

El triángulo de Sierpinski está formado por 3 copias suyas a escala r = 0.5.
Luego su dimensión de semejanza es
$$D = \frac{ln(3)}{ln(2)} \simeq 1.584962500 $$
Curva de Koch
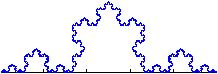
La curva de Koch está formada por 4 copias suyas a escala r = 1/3.
Luego su dimensión de semejanza es
$$D = \frac{ln(4)}{ln(3)} \simeq 1.261859507$$
Pentágono de Sierpinski

El pentágono de Sierpinski está formado por 5 copias suyas a escala
$$ r = \frac{3-\sqrt{5}}{2} $$
Luego su dimensión de semejanza es
$$D = \frac{ln(5)}{ln(\frac{2}{3-\sqrt{5}})} \simeq 1.672275938$$
Alfombra de Sierpinski

La alfombra de Sierpinski está formada por 8 copias suyas a escala r = 1/3.
Luego su dimensión de semejanza es
$$D = \frac{ln(8)}{ln(3)} \simeq 1.892789260$$
Dragón de Heighway

El dragón de Heighway está formado por 2 copias suyas a escala
$$ r =\frac{\sqrt{2}}{2} = \frac{1}{\sqrt{2}}$$
Luego su dimensión de semejanza es
$$D = \frac{ln(2)}{ln(\sqrt{2})}= 2$$
Fractal de Vicsek

El fractal de Vicsek está formado por 5 copias suyas a escala r = 0.3.
Luego su dimensión de semejanza es
$$D = \frac{ln(5)}{ln(3)} \simeq 1.464973520$$

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.
