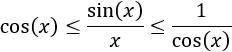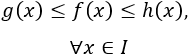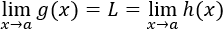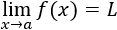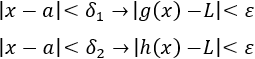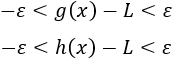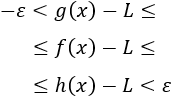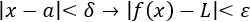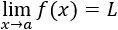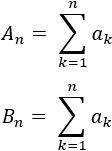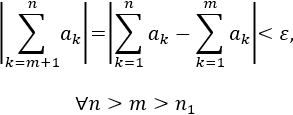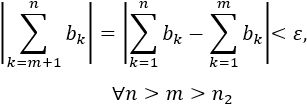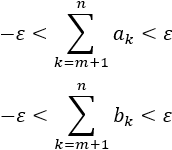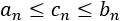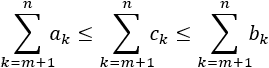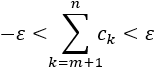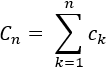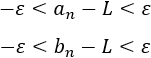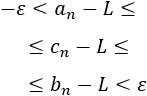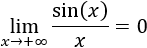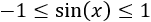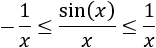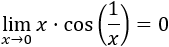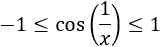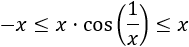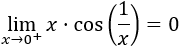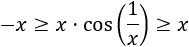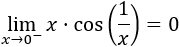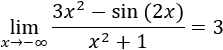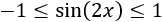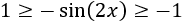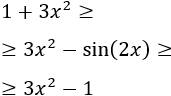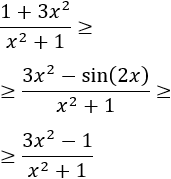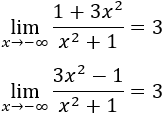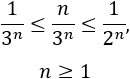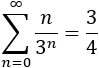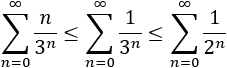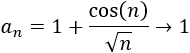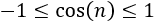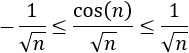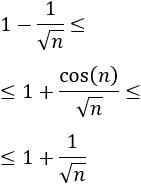Teorema del emparedado o del sándwich
En esta página enunaciamos y demostramos el teorema del emparedado. También, proporcionamos varias versiones y ejemplos de aplicación.
Contenido de esta página:
- Introducción
- Enunciado y demostración
- Versión para series
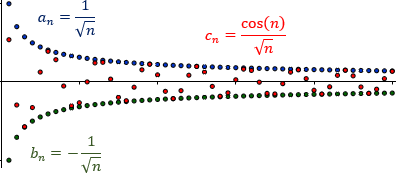
- Versión para sucesiones
- Ejemplos de aplicación
Páginas relacionadas
Otras páginas:
1. Introducción
El teorema del emparedado (también llamado teorema del sándwich, del bocadillo y de encaje, entre otros) es un resultado muy intuitivo y útil a la hora de calcular el límite de algunas funciones.
El teorema afirma que, si dos funciones tienen el mismo límite, entonces las funciones que están comprendidas entre éstas también tienen el mismo límite:
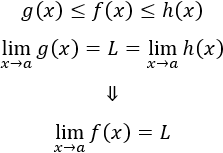
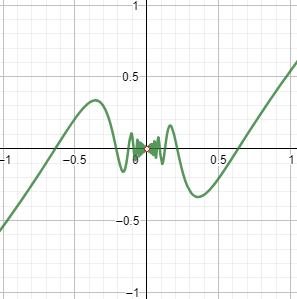
Ejemplo de gráficas de funciones encajadas (funciones \(\pm \frac{1}{2x+1}\), \(\pm \frac{1}{2x}\), \(\pm \frac{1}{x}\) y \(\pm \frac{2}{x}\)):
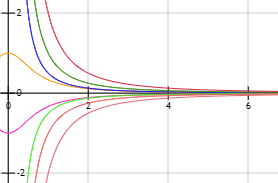
El ejemplo típico que se utiliza para mostrar la utilidad de este resultado es el cálculo del límite
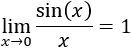
Nota: este límite es fácil de calcular, por ejemplo, aplicando la regla de L'Hôpital.
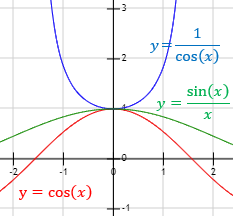
Para demostrar que el límite anterior es igual a 1 sólo hay que tener en cuenta que para \(x\) pequeños,