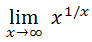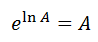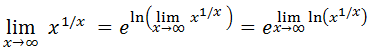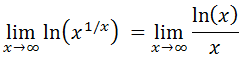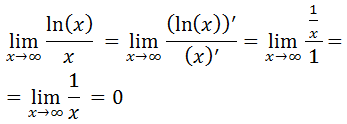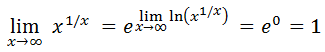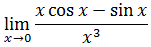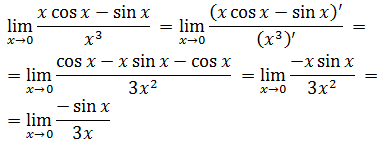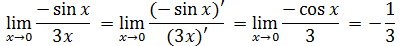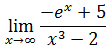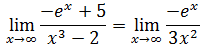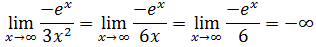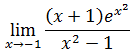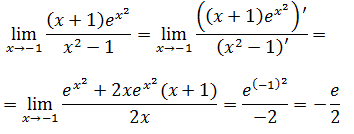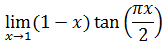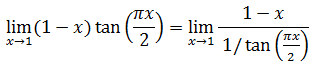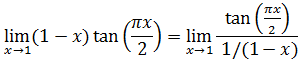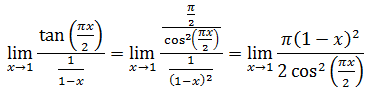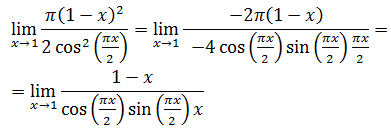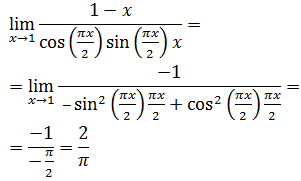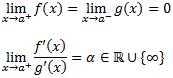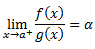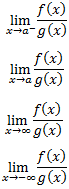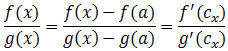Guillaume de l'Hôpital y su regla

En esta página proporcionamos una breve biografía de l'Hôpital y enunciamos y demostramos la regla de l'Hôpital. Se incluyen ejemplos de aplicación de dicha regla.

Contenido de esta página:

1. l'Hôpital y su regla
2. Ejemplos de aplicación de la Regla de l'Hôpital
3. Demostración de la primera regla de l'Hôpital

Guillaume François de l’Hôpital (1661-1704), más conocido como marqués de l’Hôpital, fue un matemático parisino conocido por la llamada Regla de l'Hôpital. Esta regla permite, como veremos a continuación, el cálculo de límites de fracciones en las que el numerador y denominador tienden ambos al infinito o a cero.

En realidad, la mecionada regla fue demostrada por Johann Bernoulli (1667-1748), pero por un acuerdo entre ambos, el descubrimiento lo publicó el marqués en su obra Analyse des infiniment petits pour l’intelligence des lignes courbes en 1696. Esta obra es considerada el primer libro publicado sobre cálculo diferencial.

El acuerdo secreto fue revelado por el propio Bernoulli que, tras la muerte del marqués, aseguró ser el verdadero autor de la mayoría de los resultados publicados por l’Hôpital. Cabe decir que, aunque se dice que l’Hôpital quiso llevarse los méritos, nunca anunció ser el descubridor y, de hecho, agradeció a Bernoulli su ayuda en su libro.

La regla sirve para calcular límites con la indeterminación 0/0 y la indeterminación infinito dividido infinito, aunque, en realidad, como veremos en los ejemplos, podemos usarla para otras indeterminaciones.

Dicho matemáticamente, de forma no rigurosa:

$$ \lim_{x \to a} \frac{f(x)}{g(x)} = \lim_{x \to a} \frac{f'(x)}{g'(x)} $$

Podemos aplicar la regla tantas veces como queramos, siempre que tengamos la indeterminación cociente de infinitos o de ceros.

La regla es cierta tanto para los límites con x tendiendo a un punto como a infinito.

Ejemplos de aplicación

Límite 1

Límite 2

Límite 3

Límite 4

Límite 5

Sean \(f\) y \(g\) dos funciones derivables en \(]a,b[\) con \(g(x)\) y \(g'(x)\) distintos de 0 y, además,

Entonces, el límite del cociente \(f(x)/g(x)\) es \(\alpha\):

El resultado es cierto también para los siguientes límites:

Demostración

Supondremos que \(\alpha\) es real, los demás casos son análogos. Definimos \(f(a) = g(a) = 0\). Entonces, \(f\) y \(g\) son continuas en \([a,b[\) y derivables en \(]a,b[\). Por el teorema del valor medio de Cauchy, para cada \(x\) existe \(c_x\) en \(]a,x[\) tal que

Sea la sucesión \(\{x_n\}^\infty_{n=1}\) contenida en \(]a,b[\) convergente a \(a\). Entonces, se tiene que la sucesión \(\{c_{x_n}\}^\infty_{n=1}\) también converge a \(a\) puesto que \(a< c_{x_n} < x_n\). Por tanto,

$$ \lim_{x\to a^+} \frac{f(x)}{g(x)} = \alpha$$