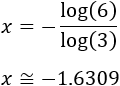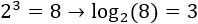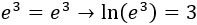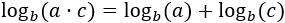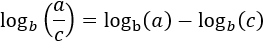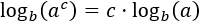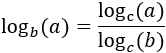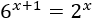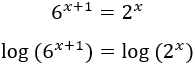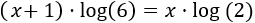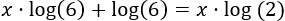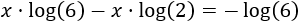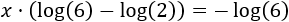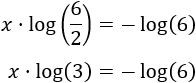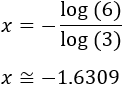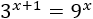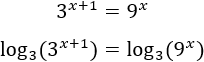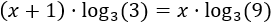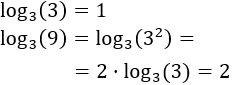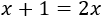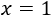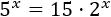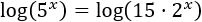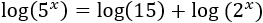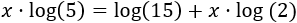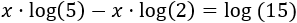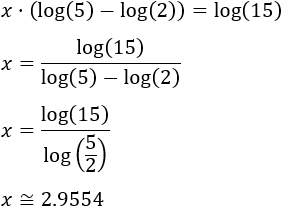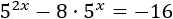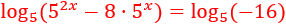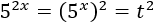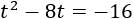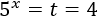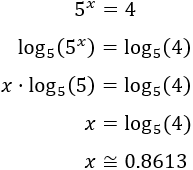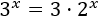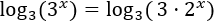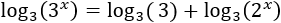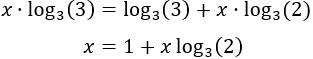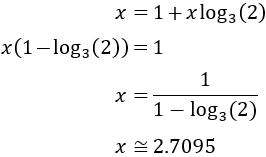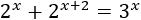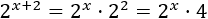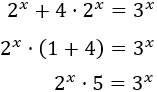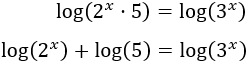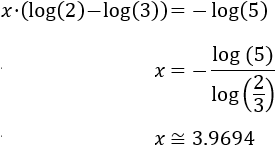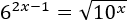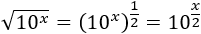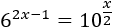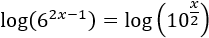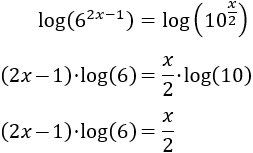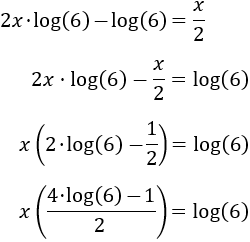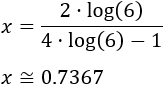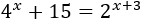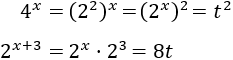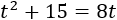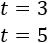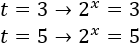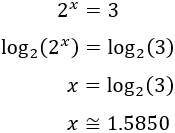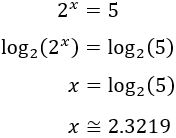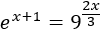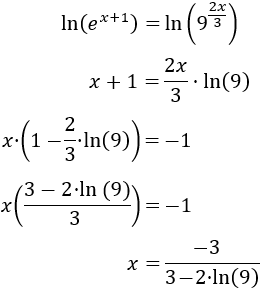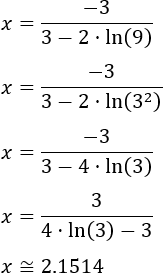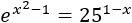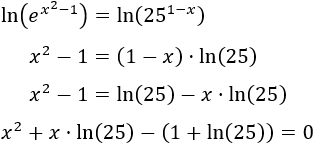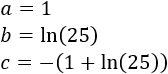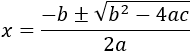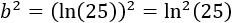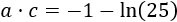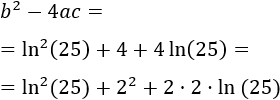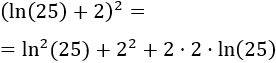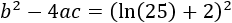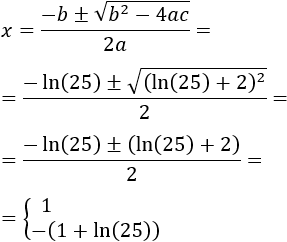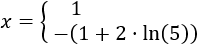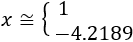Como cada autor emplea una notación, en cada ecuación indicaremos la base del logaritmo que aplicamos para evitar las confusiones. Asimismo, aproximaremos las soluciones para que sea más rápido comprobarlas si se han utilizado logaritmos en bases distintas.
Las primeras ecuaciones las explicaremos más detalladamente.
Nota: en esta página no calculamos las soluciones complejas, sólo las reales.
Ecuación 1 
Resolver con logaritmos en base 10:
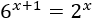
Solución:
Escribiremos el logaritmo en base 10 sin indicar explícitamente la base (es lo habitual).
Aplicamos logaritmos en base 10:
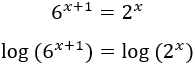
Aplicamos la propiedad del logaritmo de la potencia, la cual nos permite escribir los exponentes fuera de los logaritmos (multiplicando):
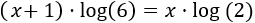
Desarrollamos el producto del lado izquierdo:
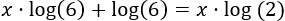
Escribimos en el lado izquierdo los sumandos en los que aparece la incógnita y los otros en el lado derecho:
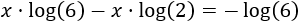
Extraemos el factor común \(x\) en el lado izquierdo:
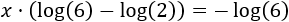
Aplicamos la propiedad de la resta de logaritmos en el lado izquierdo:
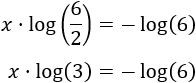
Finalmente, aislamos la incógnita:
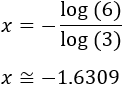
Luego la solución (real) de la ecuación exponencial es \(x = -\frac{\log(6)}{\log(3)}\).
Ecuación 2 
La siguiente ecuación se puede resolver sin aplicar logaritmos, pero se pide resolver con logaritmos en base 3:
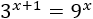
Solución:
Esta ecuación puede resolverse sin aplicar logaritmos porque podemos escribir la potencia de base 9 como una potencia de base 3 y, por tanto, tendríamos bases iguales y podríamos igualar los exponentes. Sin embargo, vamos a resolverla con logaritmos porque ésta es otra opción válida de resolución.
Aplicamos logaritmos en base 3:
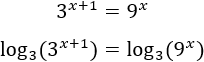
Escribimos los exponentes fuera de los logaritmos:
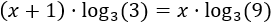
Calculamos los logaritmos que aparecen en la ecuación:
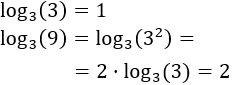
Por tanto, la ecuación queda como
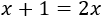
Y la solución es
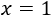
Se ha elegido logaritmo en base 3 porque las bases (3 y 9) son potencias de 3, pero podríamos haber utilizado otras bases.
Contenido de esta página en papel y en versión Kindle:
Ecuación 3 
Resolver aplicando logaritmos en base 10:
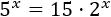
Solución:
Aplicamos logaritmos de base 10:
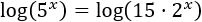
El logaritmo del lado derecho podemos escribirlo como una suma de logaritmos (logaritmo del producto):
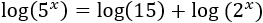
Extraemos los exponentes de los logaritmos:
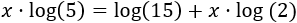
Escribimos en el lado izquierdo los sumandos que tienen la incógnita:
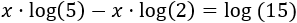
Finalmente, extraemos factor común y despejamos la incógnita:
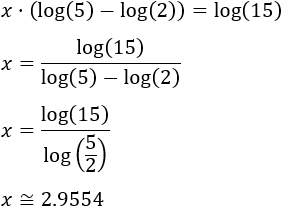
Ecuación 4 
Resolver aplicando el cambio de variable \(t = 5^x\) y logaritmos en base 5:
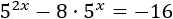
Solución:
No podemos resolver la ecuación aplicando logaritmos directamente porque tendríamos un argumento negativo, lo cual no es aceptable:
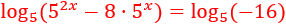
Además de esto, las propiedades de los logaritmos no permiten simplificar el logaritmo de la resta del lado izquierdo.
Si aplicamos el cambio de variable \(t = 5^x\), entonces \(5^{2x}\) queda como
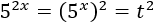
Con lo que la ecuación resultante es
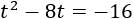
Es una ecuación de segundo grado cuya única solución es \(t = 4\).
Deshacemos el cambio de variable:
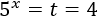
Aplicamos logaritmos en base 5 para resolver la ecuación exponencial que hemos obtenido:
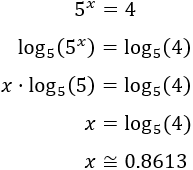
Ecuación 5 
Resolver mediante logaritmos en base 3:
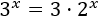
Solución:
Aplicamos directamente logaritmos en base 3:
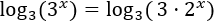
El logaritmo de la derecha puede escribirse como una suma:
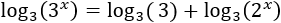
Escribimos los exponentes fuera de los logaritmos:
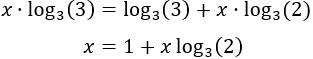
Aislamos la incógnita:
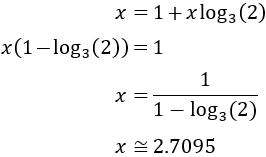
Ecuación 6 
Resolver aplicando logaritmos en base decimal (base 10):
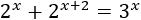
Solución:
Simplificamos la ecuación antes de aplicar logaritmos. El segundo sumando de la izquierda puede escribirse como
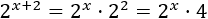
Operamos un poco en la ecuación:
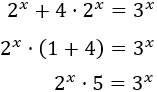
Aplicamos logaritmos en base decimal:
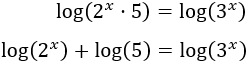
Operando de forma similar a las ecuaciones anteriores,
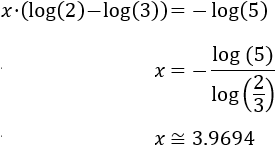
Ecuación 7 
Escribir la siguiente ecuación como una ecuación exponencial para resolverla mediante logaritmos en base decimal:
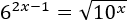
Solución:
Lo único que debemos hacer es escribir la raíz cuadrada como una potencia y aplicar la propiedad de la potencia de una potencia (multiplicar los exponentes):
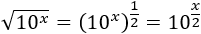
La ecuación exponencial es
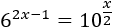
Aplicamos logaritmos en base decimal:
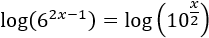
Simplificamos la ecuación aplicando las propiedades:
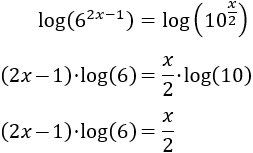
Aislamos la incógnita en el lado izquierdo:
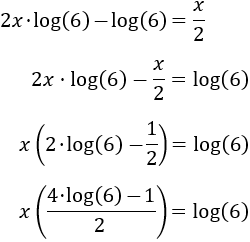
Luego la solución es
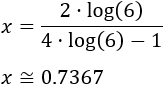
Ecuación 8 
Resolver mediante el cambio de variable \(t = 2^x\) y aplicando logaritmos en base binaria (base 2):
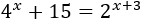
Solución:
Aplicamos el cambio de variable \(t = 2^x\):
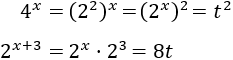
Luego la ecuación resultante es
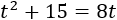
Las dos soluciones de la ecuación de segundo grado son
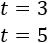
Deshacemos el cambio de variable:
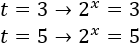
Finalmente, aplicamos logaritmos binarios para resolver las ecuaciones exponenciales obtenidas.
Primera ecuación:
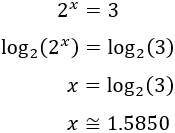
Segunda ecuación:
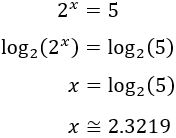
La ecuación exponencial inicial tiene dos soluciones.
Ecuación 9 
Resolver mediante logaritmos naturales (logaritmos en base \(e\), \(ln(x) = log_e (x)\)):
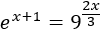
Solución:
Aplicamos logaritmos naturales directamente:
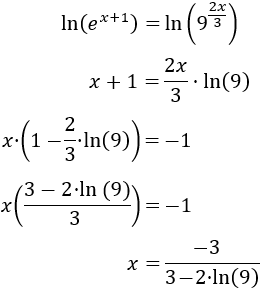
Podemos simplificar un poco más la solución escribiendo 9 como \(3^2\):
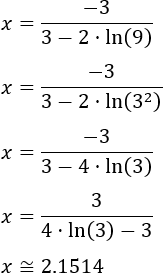
Ecuación 10 
Resolver mediante logaritmos naturales (logaritmos en base \(e\), \(ln(x) = log_e (x)\)):
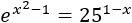
Solución:
Aplicamos logaritmos naturales:
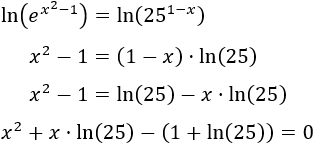
Tenemos una ecuación de segundo grado siendo sus coeficientes los siguientes:
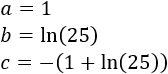
Utilizaremos la fórmula cuadrática para hallar sus soluciones:
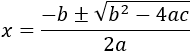
El término \(b^2\) es
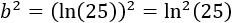
El término \(a\cdot c\) es
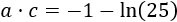
Por tanto, el radicando es
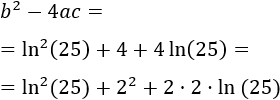
Hemos escrito el radicando como el desarrollo de una suma al cuadrado (completación de cuadrados):
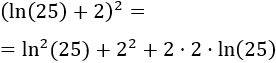
Por tanto, el radicando es
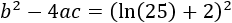
Utilizamos la fórmula para hallar las soluciones:
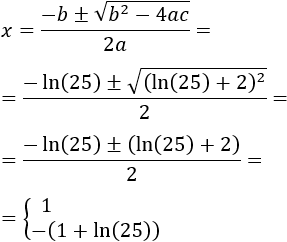
Por tanto, la ecuación exponencial tiene dos soluciones
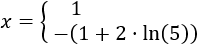
Aproximamos:
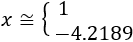
Más ecuaciones: Ecuaciones exponenciales (PyE).