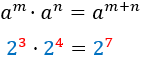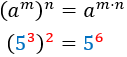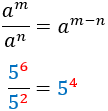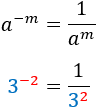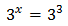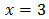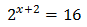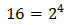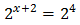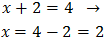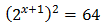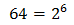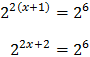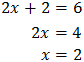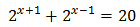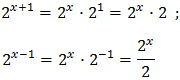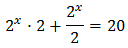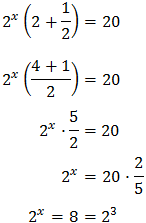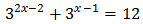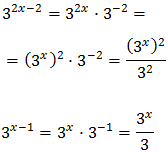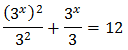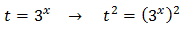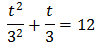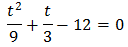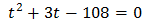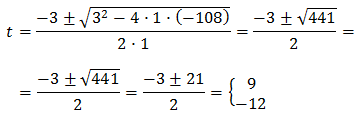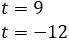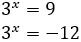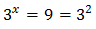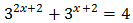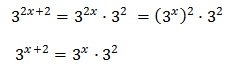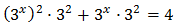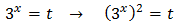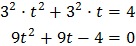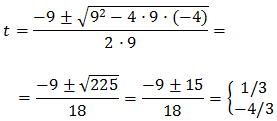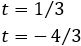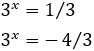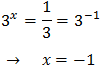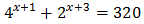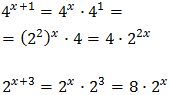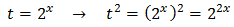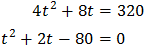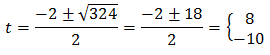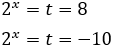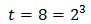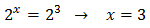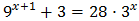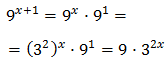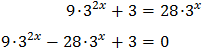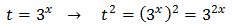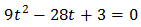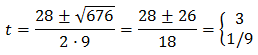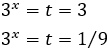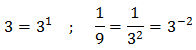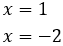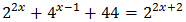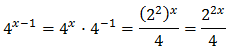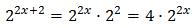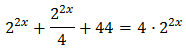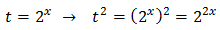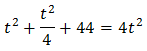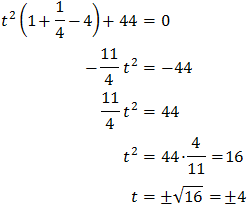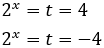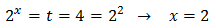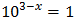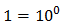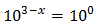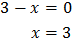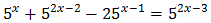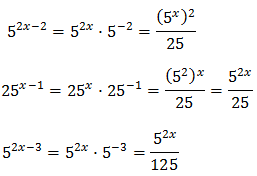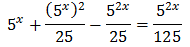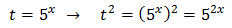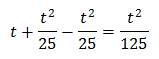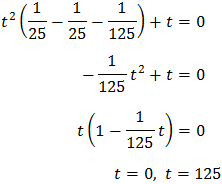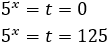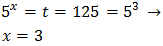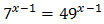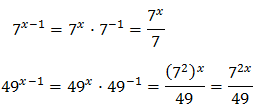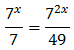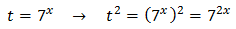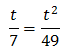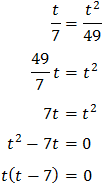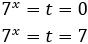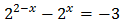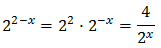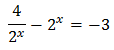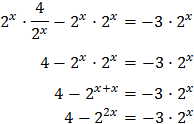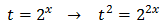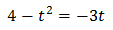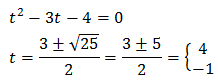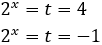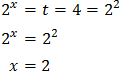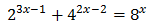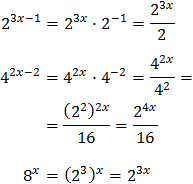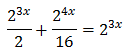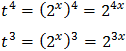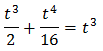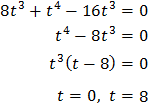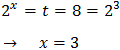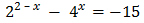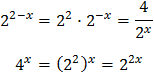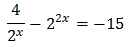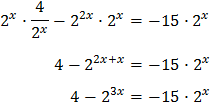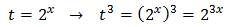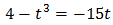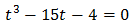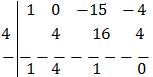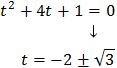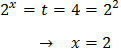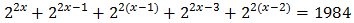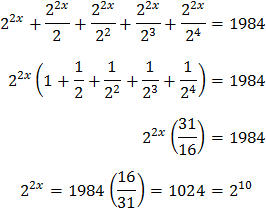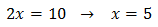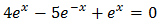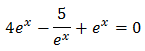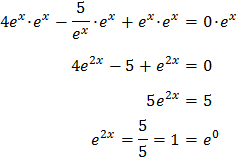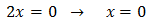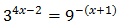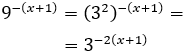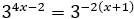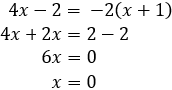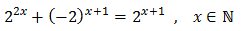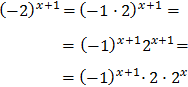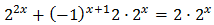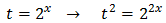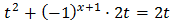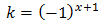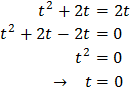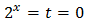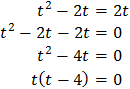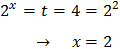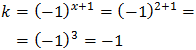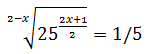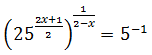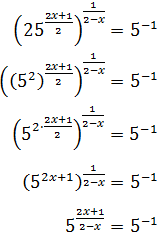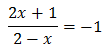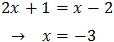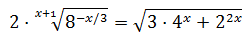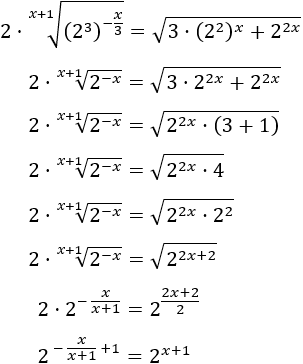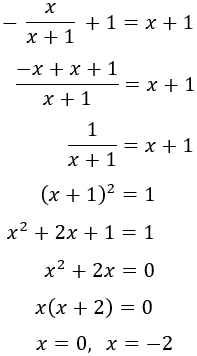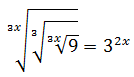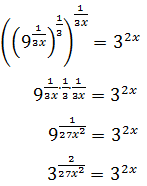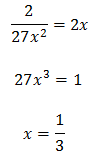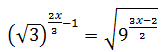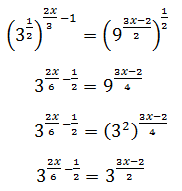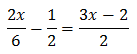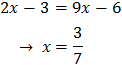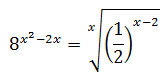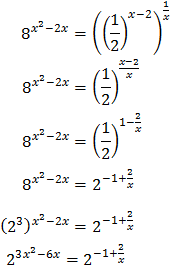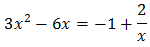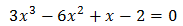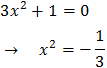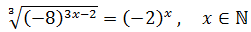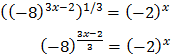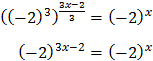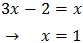A continuación, resolvemos 25 ecuaciones exponenciales de forma directa, esto es, aplicando las propiedades de las potencias y/o un cambio de variable. No resolvemos ninguna ecuación aplicando logaritmos (ejemplos de este método de resolución en ecuaciones exponenciales explicadas. Sólo consideramos las soluciones reales (no las complejas).
Ecuación 1 
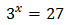
Solución
Podemos escribir 27 como la potencia \( 3^3 = 27 \) para tener potencias con la misma base (base 3):
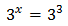
Tenemos una igualdad entre dos potencias con la misma base. Para que se cumpla, ambas potencias deben tener el mismo exponente:
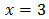
Luego la solución de la ecuación exponencial es \(x = 3\).
Ecuación 2 
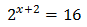
Solución
Escribimos 16 como una potencia de base 2:
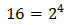
Entonces, podemos reescribir la ecuación como
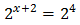
Por tanto, igualando los exponentes, tenemos una ecuación de primer grado:
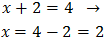
Luego la solución de la ecuación exponencial es \(x = 2\).
Contenido de esta página en papel y en versión Kindle:
Ecuación 3 
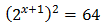
Solución
Escribimos 64 como una potencia de base 2:
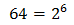
Aplicamos la propiedad de la potencia de una potencia en el lado izquierdo, multiplicando los exponentes:
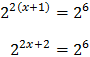
Como tenemos potencias con la misma base, podemos igualar los exponentes obteniendo una ecuación de primer grado:
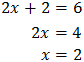
Luego la solución de la ecuación exponencial es \(x = 2\).
Ecuación 4 
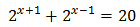
Solución
Vamos a reescribir los dos sumandos del lado izquierdo aplicando la propiedad del producto de potencias:
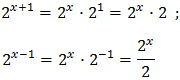
Reescribimos la ecuación:
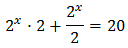
Podemos extraer el factor común \(2^x\) en el lado izquierdo y operar:
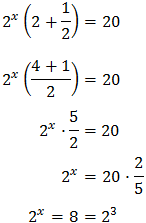
Luego la solución de la ecuación exponencial es \( x = 3\).
Ecuación 5 
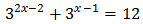
Solución
Reescribimos los sumandos de la ecuación aplicando la propiedad del producto de potencias:
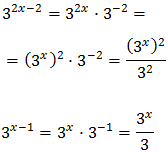
Luego podemos reescribir la ecuación como
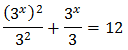
En esta ecuación no funciona extraer el factor común \(3^x\) porque, aunque tenemos \(3^x\), también tenemos \((3^x)^2\) (al cuadrado). Debemos aplicar el cambio de variable siguiente:
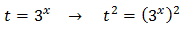
Sustituyendo en la ecuación \(3^x\) por \(t\) obtenemos
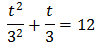
Se trata de una ecuación segundo grado completa:
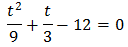
Multiplicamos por 9 la ecuación para simplificarla:
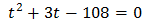
Las soluciones de esta ecuación son:
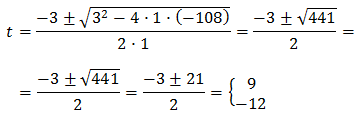
Tenemos las soluciones
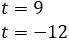
Como \(t = 3^x\), entonces
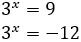
La segunda opción no es posible porque es negativa (las potencias de 3 no pueden ser negativas). Por tanto, la única solución de la ecuación exponencial debe cumplir
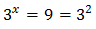
De donde obtenemos la solución de la ecuación exponencial inicial: \(x = 2\).
Ecuación 6 
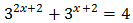
Solución
Reescribimos los sumandos:
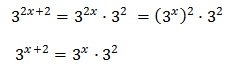
Con lo que podemos reescribir la ecuación como
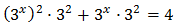
Sea el cambio de variable
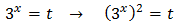
Sustituyendo en la ecuación obtenemos una ecuación de segundo grado:
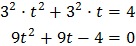
cuyas soluciones son
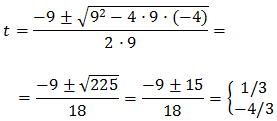
Por tanto, tenemos que
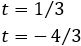
Al deshacer el cambio de variable,
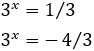
La segunda solución no es posible porque es negativa, pero la primera sí. Luego debe cumplirse
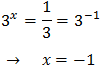
Por tanto, la solución de la ecuación exponencial es \( x = -1\).
Ecuación 7 
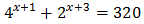
Solución
Operamos para tener potencias con la misma base:
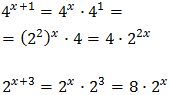
Con lo que podemos reescribir la ecuación como

Aplicamos un cambio de variable:
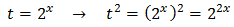
Sustituimos y obtenemos la ecuación de segundo grado
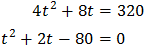
cuyas soluciones son
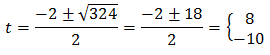
Por tanto,
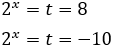
La segunda solución no es posible por ser negativa. Por tanto,
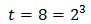
Es decir, debe cumplirse
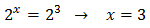
Ecuación 8 
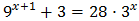
Solución
Escribimos \( 9^{x+1}\) como una potencia de base 3:
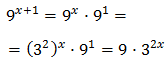
Con lo que podemos reescribir la ecuación como
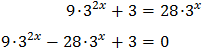
Llamamos
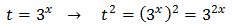
Sustituimos y obtenemos la ecuación de segundo grado
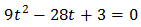
La resolvemos
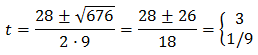
Por tanto,
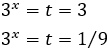
Observad que tanto \(3\) como \(1/9\) son potencias de \(3\):
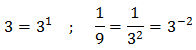
Luego la ecuación exponencial tiene dos soluciones y son
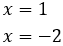
Ecuación 9 
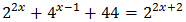
Solución
Escribimos las exponenciales como potencias de base 2:
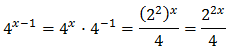
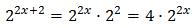
Con lo que podemos reescribir la ecuación como
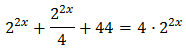
Llamamos
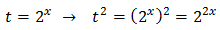
Sustituimos en la ecuación exponencial y obtenemos la ecuación de segundo grado
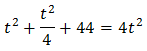
Resolvemos
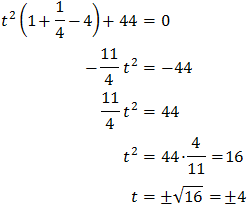
Por tanto, como \( t = 2^x\),
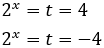
La solución \(t = -4\) no sirve por ser negativa. Luego la única solución de la ecuación exponencial es
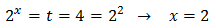
Ecuación 10 
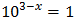
Solución
Podemos escribir 1 como una potencia de 10:
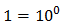
Con lo que podemos reescribir la ecuación como
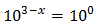
Como las bases son iguales, igualamos los exponentes:
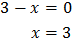
La solución de la ecuación exponencial es \(x = 3\).
Ecuación 11 
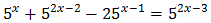
Solución
Reescribimos los sumandos del lado izquierdo aplicando la propiedad del producto de potencias:
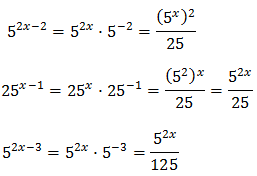
Podemos reescribir la ecuación como
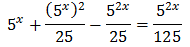
Llamamos
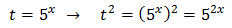
Sustituimos en la ecuación exponencial y obtenemos la ecuación de segundo grado
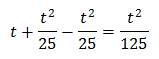
La resolvemos:
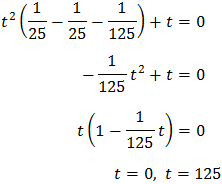
Por tanto,
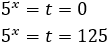
La primera, \( 5^x= 0\), no es posible por ser cero.
Luego la ecuación exponencial sólo tiene una solución:
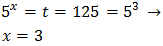
Ecuación 12 
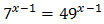
Solución
Teniendo en cuenta que
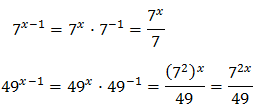
podemos reescribir la ecuación como
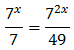
Aplicaremos el cambio de variable
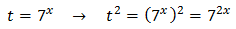
lo que proporciona la ecuación de segundo grado
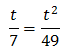
Resolvemos la ecuación:
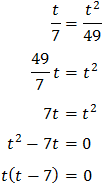
Por tanto, debe cumplirse
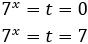
La primera igualdad no es posible por ser cero.
Por tanto, la solución de la ecuación exponencial es \(x = 1\).
Ecuación 13 
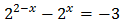
Solución
Tenemos en cuenta que
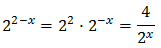
Con lo que podemos reescribir la ecuación como
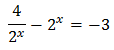
Como tenemos una exponencial dividiendo, multiplicamos toda la ecuación por ésta y así desaparece el denominador:
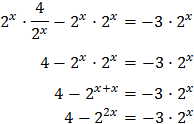
Llamamos
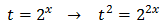
Sustituyendo, obtenemos la ecuación de segundo grado
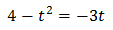
La resolvemos:
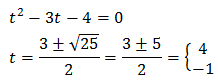
Por tanto, debe cumplirse
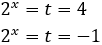
La segunda no es posible por ser negativa.
Finalmente, deshacemos el cambio de variable y resolvemos:
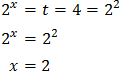
Ecuación 14 
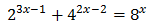
Solución
Las bases son distintas: 2, 4 y 8; pero las tres son potencias de 2.
Reescribimos las potencias:
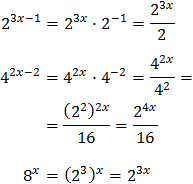
Con lo que podemos reescribir la ecuación como
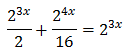
Si aplicamos el cambio de variable \( t = 2^x \), entonces:
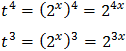
Sustituyendo, obtenemos la ecuación de cuarto grado
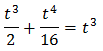
La resolvemos por factorización, extrayendo \(t^3\) como factor común:
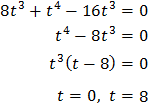
La primera no es posible por ser cero. Por tanto, la solución de la ecuación exponencial es \(x = 3\) porque
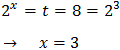
Ecuación 15 
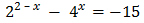
Solución
Tenemos en cuenta que
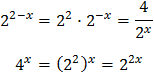
Con lo que podemos reescribir la ecuación como
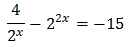
Como tenemos una exponencial dividiendo, multiplicamos toda la ecuación por ésta y así desaparece el denominador:
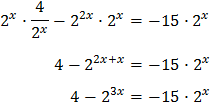
Llamamos
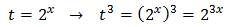
Sustituimos y obtenemos la ecuación de tercer grado
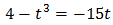
Resolvemos:
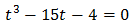
Aplicamos la regla de Ruffini:
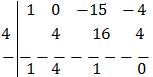
Una solución es \(t=4\). Calculamos las otras dos resolviendo la ecuación de segundo grado correspondiente:
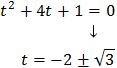
Pero éstas no son soluciones posibles ya que son negativas. Por tanto, sólo hay una solución:
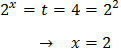
Ecuación 16 
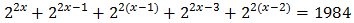
Solución
Podemos extraer el factor común \(2^{2x}\) y operar un poco:
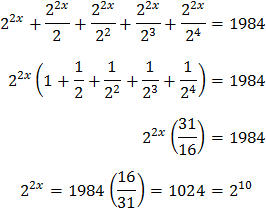
Por tanto, la ecuación exponencial se reduce a una de primer grado:
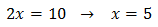
Ecuación 17 
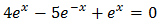
Solución
En esta ecuación, la base de las potencias es el número \(e\), pero
resolvemos del mismo modo que en los casos anteriores.
Reescribimos la ecuación:
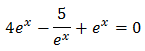
Como tenemos una exponencial en un denominador, multiplicamos toda la ecuación por ésta para que desaparezca el denominador:
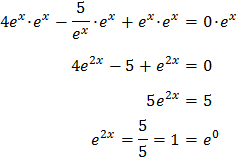
Por tanto,
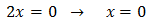
Ecuación 18 
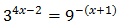
Solución
Podemos escribir el \(9\) como una potencia de base \(3\):
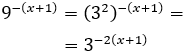
Entonces, tenemos la ecuación
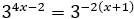
Igualamos los exponentes y resolvemos la ecuación:
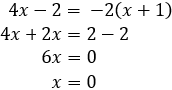
Por tanto, la solución de la ecuación exponencial es \(x = 0\).
Ecuación 19 
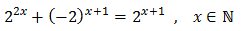
Solución
Es importante observar que la incógnita solo puede tomar valores naturales.
Debemos deshacernos del signo negativo de la base (para que las tres bases sean iguales). Lo que haremos para ello es considerar \(-2\) como el producto \(-1\cdot 2\) y aplicar la propiedad de la potencia del producto:
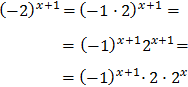
Con lo que podemos reescribir la ecuación como
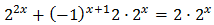
Llamamos
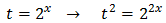
Al aplicar el cambio de variable obtenemos la siguiente ecuación de segundo grado:
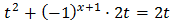
Vamos a definir una nueva variable:
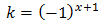
Esta variable puede tomar los siguientes valores en función del natural \(x\):
-
\(k =1\) si el exponente es par ó 0;
-
\(k =-1\) si el exponente es impar;
En primer lugar, vamos a suponer que \(k = 1\). La ecuación resultante es
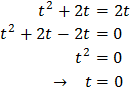
Con lo que
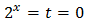
Y esto no es posible.
Supongamos ahora que \( k = -1\). La ecuación resultante es
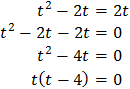
Una solución es \(t = 0\) que, como antes, no es posible. La otra es
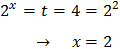
Pero hemos supuesto que \(k = -1\) y tenemos que comprobar
si esto es así cuando \(x = 2\):
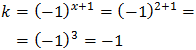
Como no hay ningún problema, la solución natural de la
ecuación exponencial es \(x = 2\).
Ecuación 20 
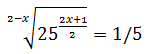
Solución
Al escribir la raíz como una potencia, la ecuación queda como
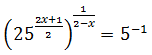
Escribimos \(25 = 5^2\) y aplicamos las propiedades de las potencias:
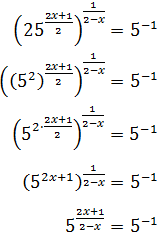
Por tanto, tenemos la ecuación
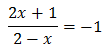
La resolvemos:
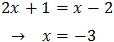
Ecuación 21 
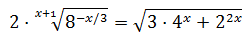
Solución
Escribimos las raíces en forma de potencias:
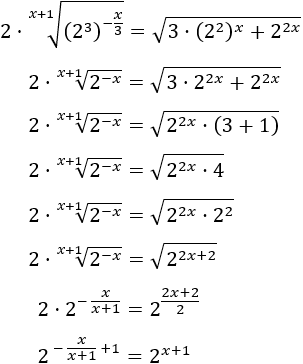
Igualamos los exponentes:
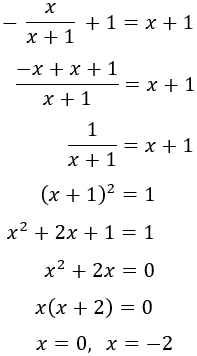
Por tanto, tenemos dos soluciones:
$$ x = 0,\ x = -2 $$
Ecuación 22 
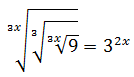
Solución
Escribimos las raíces en forma de potencias:
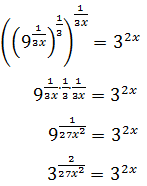
Igualamos los exponentes:
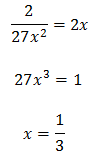
Ecuación 23 
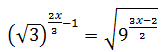
Solución
Escribimos las raíces en forma de potencia y operamos:
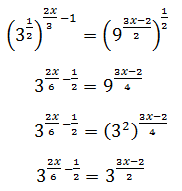
Igualando los exponentes, obtenemos una ecuación de primer grado:
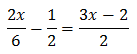
Resolvemos la ecuación obteniendo la solución de la ecuación exponencial:
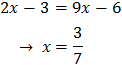
Ecuación 24 
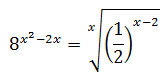
Solución
Escribimos la raíz en forma de potencia y operamos para tener bases iguales:
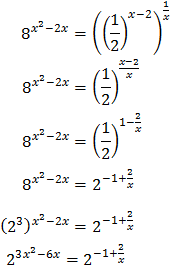
Igualamos los exponentes:
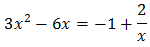
Tengamos en cuenta que x no puede ser 0 porque está en un denominador. Esto nos permite multiplicar por \( x\). Obtenemos una ecuación de tercer grado:
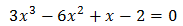
Resolvemos por Ruffini:

Una raíz es x = 2. Calculamos las otras:
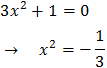
No hay raíces reales. Por tanto, la única solución real de
la ecuación exponencial es \(x = 2\).
Ecuación 25 
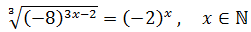
Nota: se busca una solución natural (\(x\in\mathbb{N}\)).
Solución
Escribimos la raíz en forma de potencia. La ecuación queda como:
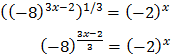
Podemos escribir -8 como \(-8 = (-2)^3\). Así,
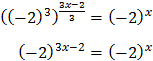
Igualamos los exponentes:
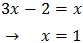
Más ecuaciones: Ecuaciones exponenciales explicadas (PyE).