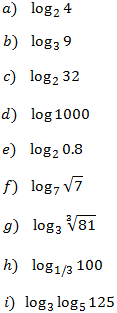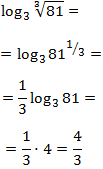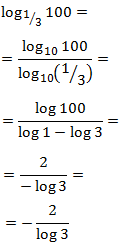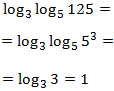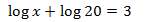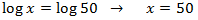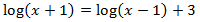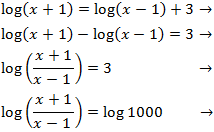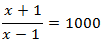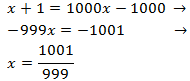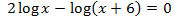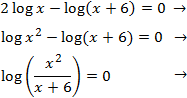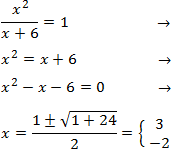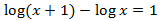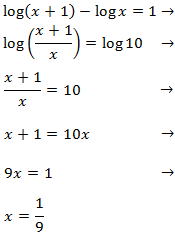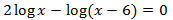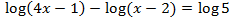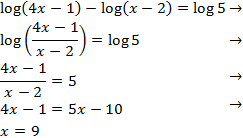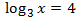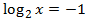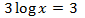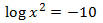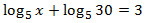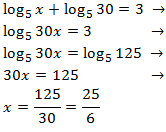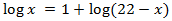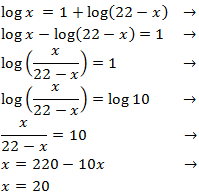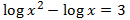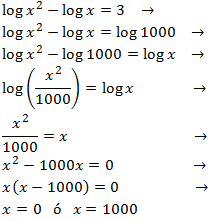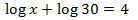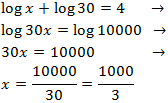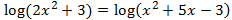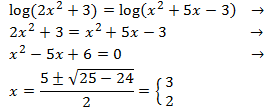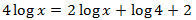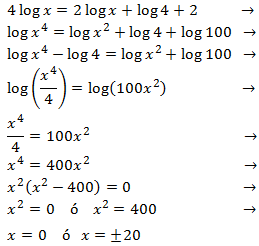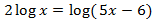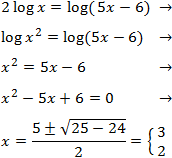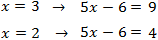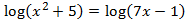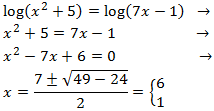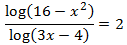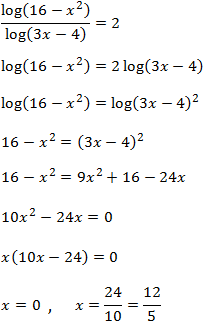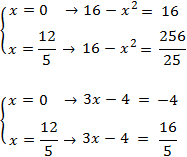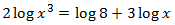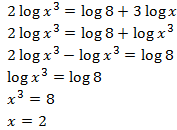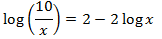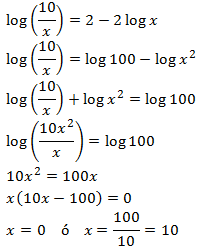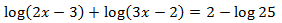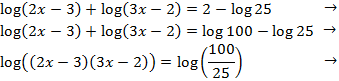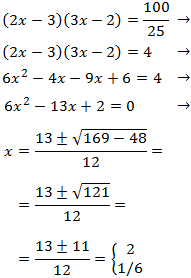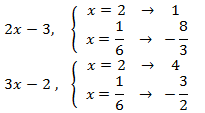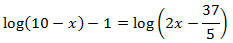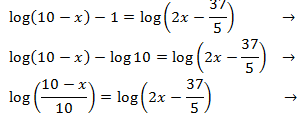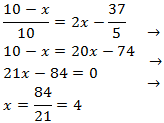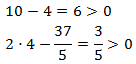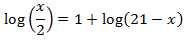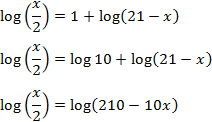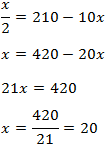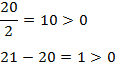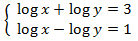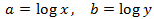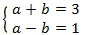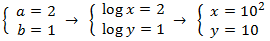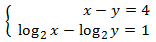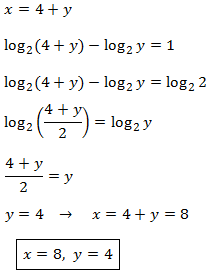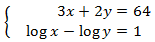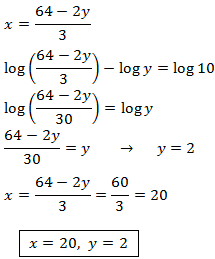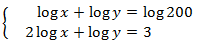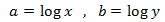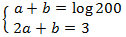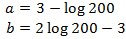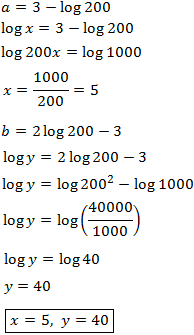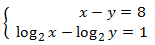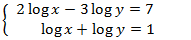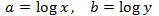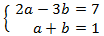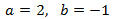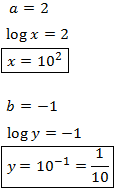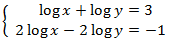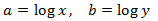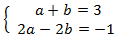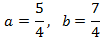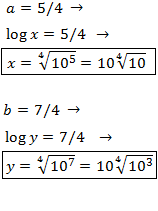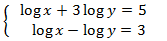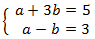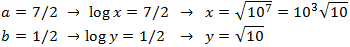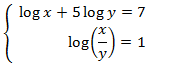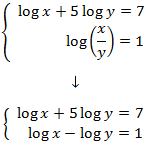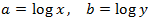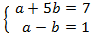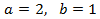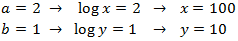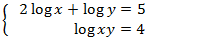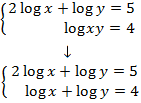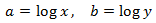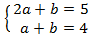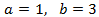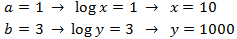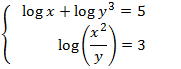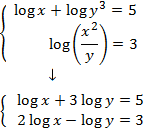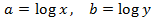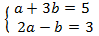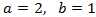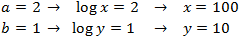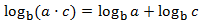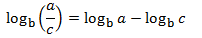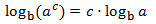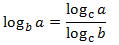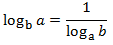Nota previa: por comodidad, omitiremos el paréntesis del argumento del logaritmo cuando sea posible. Es decir, escribiremos, por ejemplo, \( \log a\) en lugar de \( \log(a)\).
Ejercicio previo 
Calcular los siguientes logaritmos:
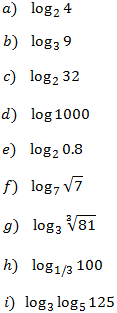
Ver solución
Recordad que el logaritmo en base \(b\) de una potencia de \(b\) es su exponente:
$$ \log_b (b^a) = a $$
-
Escribimos 4 como \(2^2\):
$$ \log_2(4) = $$
$$ = \log_2(2^2) = 2 $$
-
Escribimos 9 como \(3^2\):
$$ \log_3(9) = $$
$$ = \log_3 (3^2) = 2$$
-
Escribimos 32 como la potencia \(2^5\):
$$ \log_2 (32) = $$
$$ = \log_2(2^5) = 5 $$
-
Escribimos 1000 como la potencia \(10^3\):
$$ \log(1000) =$$
$$ = \log_{10} (1000)= $$
$$ = \log_{10}(10^3) =3 $$
-
El número decimal 0.8 es la fracción \(8/10\):
$$ \log_2(0.8) = $$
$$ =\log_2 \left( \frac{8}{10} \right) =$$
$$ = \log_2 (8) - \log_2(10) = $$
$$ = \log_2 (2^3) - \log_2(2·5) = $$
$$ = 3 -( \log_2 (2·5) ) = $$
$$ = 3 - (\log_2(2) + \log_2(5))= $$
$$ = 3 - (1+\log_2(5)) = $$
$$ = 2 -\log_2(5) $$
-
Escribimos el argumento como una potencia de 7:
$$ \log_7(\sqrt{7}) = \log_7(7^{\frac{1}{2}}) = $$
$$ =\frac{1}{2} \cdot \log_7(7) = $$
$$= \frac{1}{2}\cdot 1 $$
-
Escribimos la raíz como una potencia para extraer su exponente:
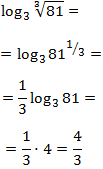
-
Cambiamos el logaritmo a base 10:
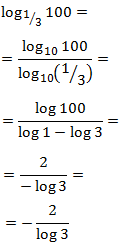
-
Escribimos \(25\) como una potencia:
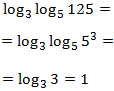
Ecuación 1 
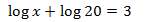
SOLUCIÓN
Lo primero que hacemos es escribir el número 3 como un logaritmo en base 10:
$$ \log (1000) = \log (10^3) = 3$$
La ecuación que queda es:
$$ \log x + \log 20 = \log 1000 $$
$$ \log x = \log 1000 - \log 20 $$
Aplicamos la propiedad de la resta de logaritmos:
$$ \log x = \log \left( \frac{1000}{20} \right) $$
$$ \log x = \log 50 $$
Tenemos una igualdad entre logaritmos (en la misma base), entonces los argumentos (lo de dentro) tienen que
ser iguales:
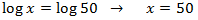
La solución es \(x = 50\).
Ecuación 2a 

$$ \log(x^2) = \log(x) $$
Igualamos los argumentos:
$$ x^2 = x $$
Las soluciones de la ecuación de segundo grado incompleta \(x^2 - x = 0\) son \(x=0\) y \(x=1\).
Ahora bien, observemos los argumentos de los logaritmos de la ecuación inicial:
-
Un argumento es \(x^2\).
-
El otro argumento es \(x\).
En ambos casos, los argumentos son iguales a 0 cuando \(x = 0\), pero sabemos que no existe el logaritmo de un número no positivo. Por tanto, la solución \(x = 0\) ha de ser descartada.
Luego la única solución de la ecuación logarítmica es \(x = 1\).
Ecuación 2b 
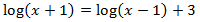
SOLUCIÓN
Escribimos 3 como un logaritmo:
$$3=\log(10^3)=\log(1000)$$
Esto nos permitirá sumar los logaritmos:
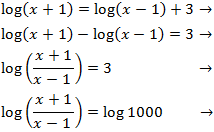
Los logaritmos son iguales cuando sus argumentos iguales. Es decir,
tenemos la ecuación
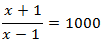
Resolvemos la ecuación:
El denominador pasa multiplicando al otro lado:
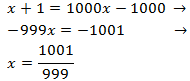
De nuevo hemos calificado esta ecuación como difícil porque debemos tener en cuenta los argumentos de los logaritmos de la ecuación inicial:
-
Un argumento es \(x+1\), que siempre es positivo (positivo + positivo = positivo)
-
El otro argumento es \(x-1\) que, al ser una resta, podría ser no positivo (negativo o cero) según el valor que tome \(x\). Por eso debemos comprobar que el valor hallado para \(x\) no hace que este argumento sea no positivo:
$$x-1 = \frac{1001}{999}-1 \simeq 0.002 > 0 $$
Como los argumentos son positivos, la solución de la ecuación logarítmica es \(x = 1001/999\).
Ecuación 3 
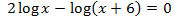
SOLUCIÓN
El 2 que multiplica al logaritmo puede introducirse como el exponente de su argumento. Así, podremos sumar los logaritmos:
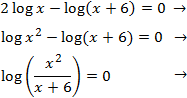
Recordad que un logaritmo es 0 cuando su argumento es 1, por tanto, igualamos el argumento a 1 y resolvemos la ecuación de segundo grado obtenida:
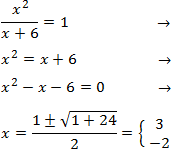
Observad que la única solución posible es \(x = 3\) ya que los argumentos tienen que ser positivos.
Ecuación 4 
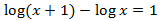
SOLUCIÓN
Escribimos 1 como el logaritmo de 10 para poder aplicar las propiedades de los logaritmos e igualar los argumentos:
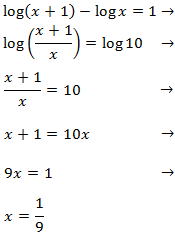
La solución de la ecuación logarítmica es \( x = 1/9\).
Ecuación 5 
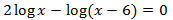
SOLUCIÓN
El 2 que multiplica al logaritmo puede entrar como exponente de su argumento:
$$ \log(x^2) = \log(x-6) $$
Igualamos los argumentos:
$$ x^2 = x - 6 $$
Resolvemos la ecuación de segundo grado completa:
$$ x^2 -x + 6 = 0 $$
$$ x=\frac{1\pm \sqrt{1-24}}{2} $$
Como el discriminante es negativo (-23), no hay soluciones (reales). Por tanto, la ecuación logarítmica no tiene solución (real), por eso la hemos calificado como difícil.
Ecuación 6 
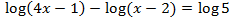
SOLUCIÓN
Al escribir la resta de logaritmos como un único logaritmo, tenemos una igualdad entre logaritmos y, por tanto, podemos igualar sus argumentos:
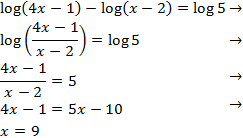
La solución de la ecuación logarítmica es \(x = 9\).
Ecuación 7 
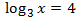
SOLUCIÓN
Escribimos el 4 como un logaritmo de base 3:
$$ \log_3 (x) = \log_3(3^4) $$
Como tenemos una igualdad entre logaritmos de igual base, igualamos sus argumentos:
$$ x = 3^4 $$
Por tanto, \(x = 3^4=81\) es la solución de la ecuación logarítmica.
Ecuación 8 
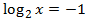
SOLUCIÓN
Escribimos -1 como un logaritmo en base 2:
$$ \log_2(x) = -1 $$
$$ \log_2 (x) = \log_2 (2^{-1}) $$
Igualamos argumentos:
$$ x = 2^{-1} = \frac{1}{2} $$
Nota: recordad que para poder igualar los argumentos, los logaritmos tienen que tener la misma base.
Ecuación 9 
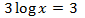
SOLUCIÓN
Escribimos el coeficiente 3 como el exponente del argumento:
$$ \log(x^3) = 3 $$
Escribimos el 3 de la derecha como un logaritmo:
$$ \log(x^3) = \log(10^3) $$
Igualamos argumentos:
$$ x^3 = 10^3 $$
Por tanto, solución de la ecuación logarítmica es \(x = 10\).
Ecuación 10 
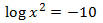
SOLUCIÓN
Escribimos -10 como un logaritmo:
$$ \log(x^2) = \log(10^{-10}) $$
Igualamos argumentos:
$$ x^2 = 10^{-10} $$
Por tanto, haciendo la raíz cuadrada:
$$ x = \pm \sqrt{10^{-10}} $$
$$ x = \pm 10^{-10/2} $$
$$ x = \pm 10^{-5} $$
Como el argumento del logaritmo es \(x^2\), siempre es positivo (salvo que \(x\) fuera 0). Por tanto, ambas soluciones halladas son
realmente soluciones de la ecuación logarítmica.
Luego la ecuación logarítmica tiene dos soluciones:
- Una solución es \(x = 10^{-5}\).
- La otra solución es \(x = -10^{-5}\).
Ecuación 11 
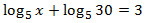
SOLUCIÓN
Escribimos el número 3 como un logaritmo en base 5:
$$ 3 = \log_5 (5^3) = \log_5(125) $$
Así, podremos obtener una igualdad entre logaritmos con la misma base:
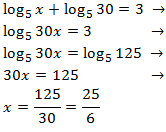
La solución de la ecuación logarítmica es \( x = 25/6\).
Ecuación 12 
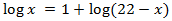
SOLUCIÓN
Escribimos 1 como el logaritmo \(\log(10)\) y operamos un poco para obtener una igualdad entre logaritmos:
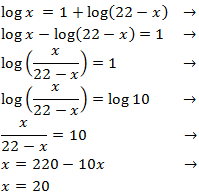
La solución de la ecuación logarítmica es \(x = 20\).
Ecuación 13 
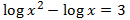
SOLUCIÓN
Escribimos 3 como el logaritmo \(\log(1000)\), restamos los logaritmos e igualamos los argumentos:
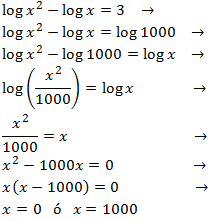
La única solución de la ecuación logarítmica es \(x = 1000\) ya que el
argumento de un logaritmo nunca puede ser cero.
Ecuación 14 
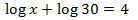
SOLUCIÓN
Escribimos 4 como un logaritmo:
$$ \log(10000) = \log(10^4) = 4 $$
Entonces,
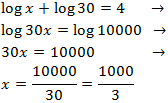
Ecuación 15 
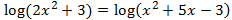
SOLUCIÓN
Igualamos los argumentos (lo de dentro del logaritmo) y resolvemos la ecuación de segundo grado:
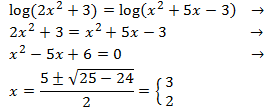
Por tanto, los argumentos coinciden cuando \(x = 3\) o cuando \(x = 2\). Pero recordad comprobar que los argumentos son positivos para estos valores de \(x\).
Las soluciones de la ecuación logarítmica son \(x = 3\) y \(x = 2\).
Ecuación 16 
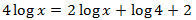
SOLUCIÓN
Los coeficientes 4 y 2 pueden entrar dentro de los logaritmos como exponentes; el 2 de la derecha lo escribimos como \(\log(100)\):
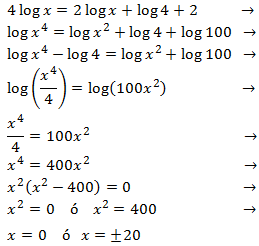
De las tres posibles soluciones, la única que es solución de la ecuación logarítmica es \(x = 20\) porque las otras hacen que los argumentos sean negativos ó 0.
Ecuación 17 
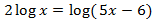
SOLUCIÓN
Introducimos el 2 como exponente del argumento e igualamos los argumentos:
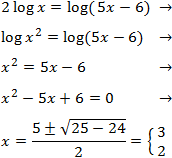
Comprobamos que el argumento \(5x-6\) es positivo para las dos soluciones obtenidas:
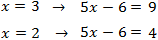
Las dos raíces de la ecuación son soluciones de la
ecuación logarítmica.
Ecuación 18 
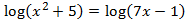
SOLUCIÓN
Igualamos los argumentos y resolvemos la ecuación de segundo grado:
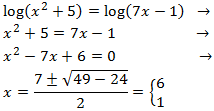
Las dos raíces obtenidas son solución de la ecuación logarítmica.
Ecuación 19 
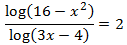
SOLUCIÓN
Antes que nada, observad que el argumento del logaritmo del denominador no puede ser 1 (para no dividir entre 0).
Pasamos el logaritmo del denominador multiplicando al otro lado, elevamos al cuadrado su argumento e igualamos los argumentos:
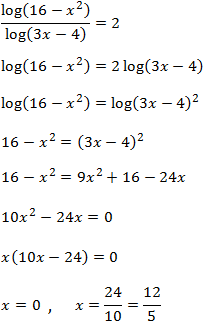
La única solución es \(x = 12/5\) porque si \(x = 0\), el
argumento del logaritmo del denominador es negativo:
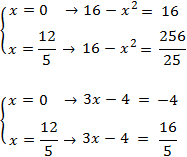
Ecuación 20 
SOLUCIÓN
Al introducir el 3 en el argumento podemos restar dos logaritmos:
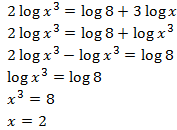
La solución de la ecuación logarítmica es \(x = 2\).
Ecuación 21 
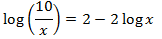
SOLUCIÓN
Observad que \(x\) no puede ser 0 (para no anular el argumento del logaritmo de la derecha y porque se encuentra en un denominador).
Escribimos 2 como \( \log 100\), introducimos el otro 2 en el argumento y operamos un poco:
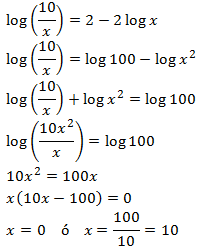
La única solución de la ecuación logarítmica es \(x = 10\).
Ecuación 22 
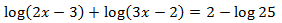
SOLUCIÓN
El 2 de la derecha lo podemos escribir como un logaritmo:
$$2 = \log (10^2)= \log(100)$$
Sumaremos los logaritmos de la izquierda y restaremos los de la derecha:
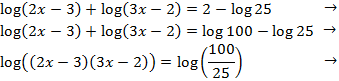
Como tenemos una igualdad entre logaritmos, igualamos sus argumentos y resolvemos la ecuación de segundo grado obtenida:
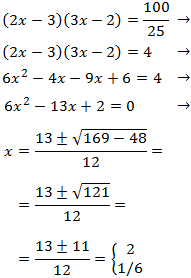
Comprobamos si los argumentos son positivos para estas dos (posibles) soluciones :
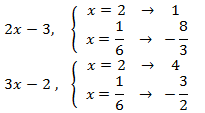
Por tanto, la única solución es \(x = 2\).
Ecuación 23 
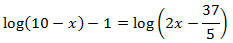
SOLUCIÓN
Escribimos 1 como el logaritmo \( \ log 10 \):
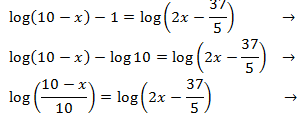
Igualamos los argumentos y resolvemos la ecuación:
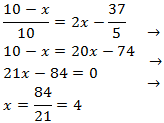
Comprobamos que los argumentos son positivos para la solución obtenida:
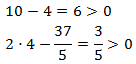
La solución de la ecuación logarítmica es \(x = 4\).
Ecuación 24 
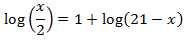
SOLUCIÓN
Escribimos 1 como el logaritmo \( \log 10\):
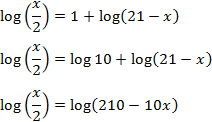
Igualamos los argumentos y resolvemos la ecuación:
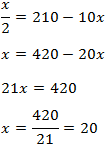
Comprobamos si los argumentos de los logaritmos son positivos cuando \(x = 20\):
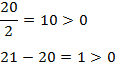
Ecuación 25 
$$ \log_x(\sqrt{3}) = 5 $$
SOLUCIÓN
En esta ecuación tenemos la incógnita en la base del logaritmo.
Escribimos el 5 como un logaritmo en base \(x\):
$$ \log_x(\sqrt{3}) = \log_x(x^5) $$
Igualamos argumentos:
$$ x^5 = \sqrt{3} $$
Por tanto,
$$ x = \sqrt[5]{\sqrt{3}} $$
O bien, si queremos
$$ x = \sqrt[10]{3} $$
Más
ecuaciones logarítmicas resueltas.
Vamos a resolver sistemas de 2 ecuaciones logarítmicas con 2 incógnitas.
En general, el método de resolución que seguiremos es:
-
Aplicar un cambio de variable para transformar las ecuaciones logarítmicas en ecuaciones lineales.
-
Resolver el sistema de ecuaciones lineales.
-
Deshacer el cambio de variable (lo que conlleva resolver ecuaciones logarítmicas).
Sistema 1 
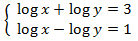
SOLUCIÓN
Aplicamos el cambio de variable
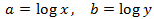
obteniendo el sistema de ecuaciones lineales
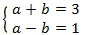
Resolvemos el sistema y deshacemos el cambio de variable:
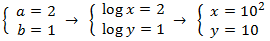
Sistema 2 
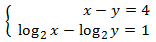
SOLUCIÓN
Nótese que la primera ecuación del sistema no
es logarítmica.
Aislamos x en la primera ecuación y la sustituimos
en la segunda:
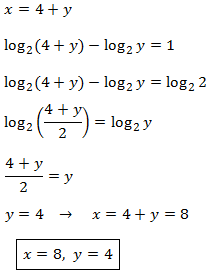
Sistema 3 
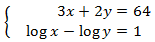
SOLUCIÓN
Este sistema es similar al anterior:
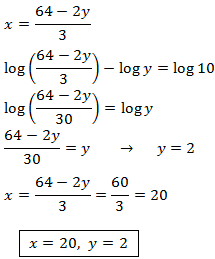
Sistema 4 
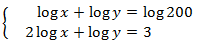
SOLUCIÓN
Aplicamos el cambio de variable
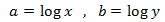
El sistema de ecuaciones lineales resultante es
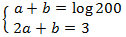
La solución de este sistema es:
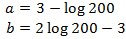
Deshacemos el cambio de variable y
obtenemos la solución del sistema inicial:
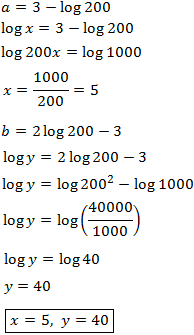
Sistema 5 
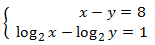
SOLUCIÓN
Aislamos \(x\) en la primer ecuación, sustituimos en la segunda y resolvemos la ecuación logarítmica:

Sistema 6 
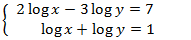
SOLUCIÓN
Aplicamos el cambio de variable
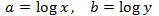
El sistema que obtenemos es
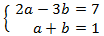
La solución del sistema es
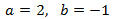
Deshacemos el cambio de variable y
obtenemos la solución del sistema de ecuaciones logarítmicas:
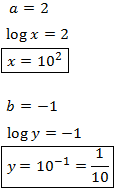
Sistema 7 
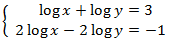
SOLUCIÓN
Aplicamos el siguiente cambio de variable:
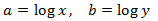
El sistema resultante es
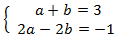
La solución de este sistema es:
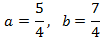
Ahora deshacemos el cambio de variable y
obtenemos la solución del sistema inicial:
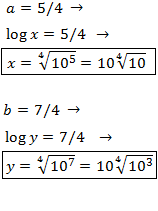
Sistema 8 
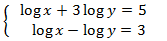
Ver solución
Aplicamos un cambio de variable:

Así obtenemos el siguiente sistema de ecuaciones lineales
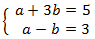
cuya solución es

Finalmente, deshacemos el cambio de variable
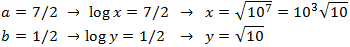
No es necesario comprobar el signo de los argumentos ya que los valores obtenidos son positivos.
Sistema 9 
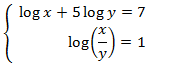
Ver solución
Primero aplicamos la regla del logaritmo del cociente:
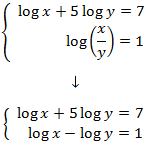
Aplicamos un cambio de variable:
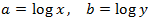
Así obtenemos el siguiente sistema de ecuaciones lineales
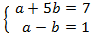
cuya solución es
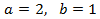
Finalmente, deshacemos el cambio de variable
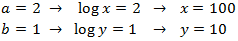
No hace falta comprobor el signo de los argumentos.
Sistema 10 
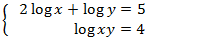
Ver solución
Aplicamos la propiedad del logaritmo del producto:
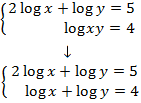
Ahora aplicamos el cambio de variable
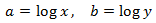
Obteniendo así el sistema
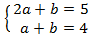
cuya solución es
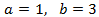
Finalmente, deshacemos el cambio de variable
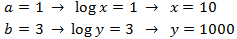
No es necesario comprobar el signo de los argumentos.
Sistema 11 
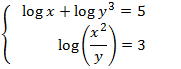
Ver solución
Aplicamos la propiedad del logaritmo del cociente y de la potencia:
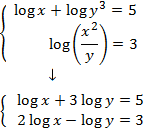
Ahora aplicamos el cambio de variable
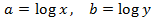
Obteniendo así el sistema
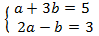
cuya solución es
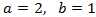
Finalmente, deshacemos el cambio de variable
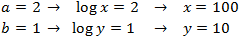
Más
sistemas de ecuaciones logarítmicas.