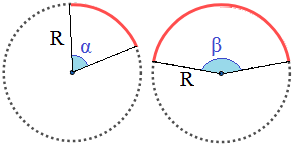
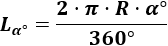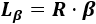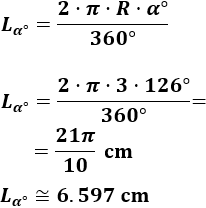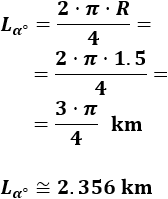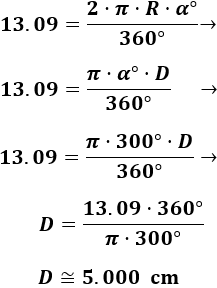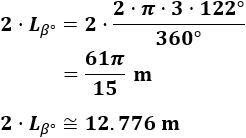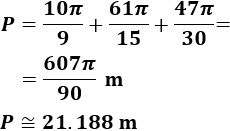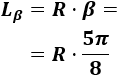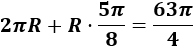Problema 1
Calcular la longitud del siguiente arco (radio \(R=3\) cm y ángulo \(\alpha =126^\circ\)):
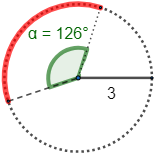
Ver solución
Utilizamos la fórmula con el ángulo en grados:
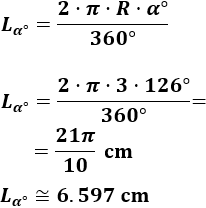
Problema 2
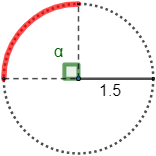
Calcular la longitud del siguiente arco (radio \(R=1.5\) km y ángulo \(\alpha = \pi /2\) rad):
Ver solución
No es necesario utilizar la fórmula porque la longitud del arco es una cuarta parte de la longitud de la circunferencia:
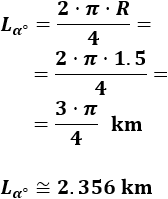
Problema 3
Calcular el diámetro de la muñeca de Ana si su pulsera magnética (que le viene ajustada) mide \(13.09\) cm:
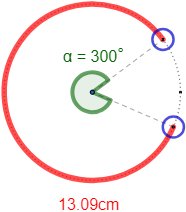
Ver solución
La fórmula de la longitud de arco con el ángulo en grados es
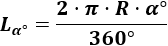
Sustituimos el producto \(2·R\) de la fórmula por \(D\) (diámetro de la circunferencia) y resolvemos la ecuación:
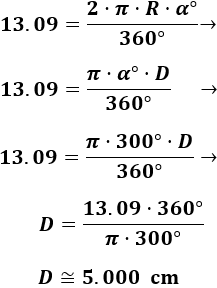
Por tanto, el diámetro de la meñeca de Ana mide 5cm.
Problema 4
Calcular el perímetro (en azul) de la siguiente figura construida con arcos de circunferencias de radios 1, 2 y 3 metros:
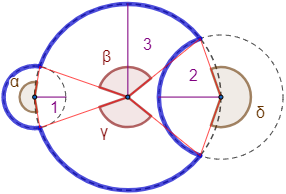
Los ángulos son \(\alpha =200^\circ\), \(\beta =122^\circ\), \(\gamma =122^\circ\) y \(\delta =219^\circ\).
Ver solución
En total hay 4 arcos de circunferencia.
La longitud del arco de la izquierda (con radio \(R=1\) y ángulo \(\alpha =200^\circ \)) es

Los arcos de la circunferencia central tienen el mismo ángulo, así que la suma de sus longitudes es
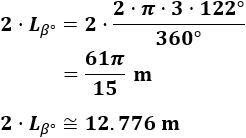
El ángulo \(\delta \) no es el ángulo del arco que nos falta, sino el de su conjugado. El ángulo del arco es \(360^\circ - \delta = 141^\circ\). Por tanto, su longitud es

Finalmente, calculamos la el perímetro de la figura sumando las longitudes de todos los arcos:
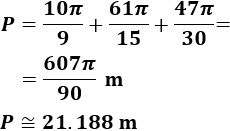
Problema 5
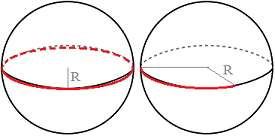
Se tiene una cuerda roja que mide \(63\pi /4\) metros (aproximadamente, \(49.48\) metros) y se utiliza para rodear con una única vuelta una esfera metálica de radio \(R\) metros por su ecuador.
Se corta el trozo de cuerda que sobra y se intenta hacer lo mismo con una esfera idéntica, pero sólo hay suficiente para un arco de \(5\pi /8\) radianes.
¿Cuánto mide el radio \(R\) de las esferas?
Ver solución
La longitud de la cuerda que rodea completamente a la esfera mide \(2\pi R\).
Como con el trozo restante se forma un arco de \(5\pi /8\) radianes, su longitud es
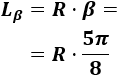
En total, la cuerda mide (antes de cortarla)
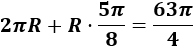
Resolvemos la ecuación:

Por tanto, el radio de las esferas mide 6 metros.