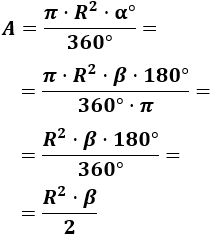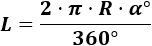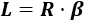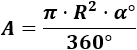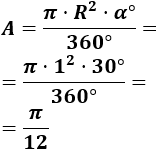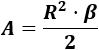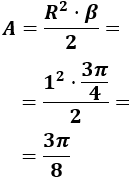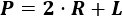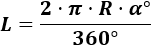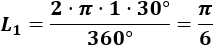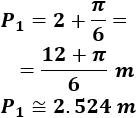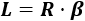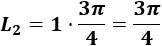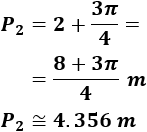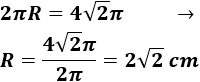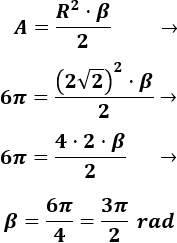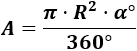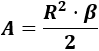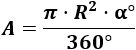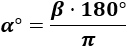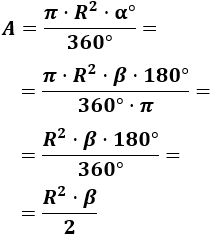Problema 1
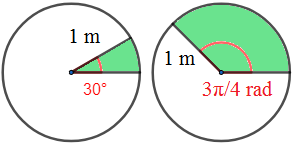
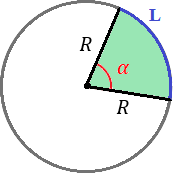
Calcular el área del sector circular de una circunferencia de radio 1 metro y ángulo
-
\(\alpha = 30^\circ\)
-
\(\beta = 3\pi /4\ rad\)
Ver solución
-
\(\alpha = 30^\circ\)
Para el ángulo en grados utilizamos la fórmula
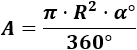
Sustituimos los datos:
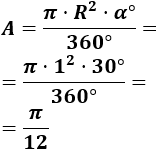
El área del sector circular es \(\pi /12 m^2\). Es decir, aproximadamente, \(0.262 m^2\).
-
\(\beta = 3\pi /4\ rad\)
Para el ángulo en radianes utilizamos la fórmula
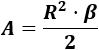
Sustituimos los datos:
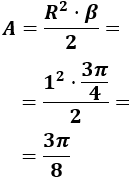
El área del sector circular es \(3\pi/8 m^2\). Es decir, aproximadamente, \(1.178 m^2\).
Problema 2
Calcular el perímetro de los sectores circulares del problema anterior.
Ver solución
Para calcular el perímetro utilizamos la fórmula
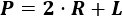
donde \(L\) es la longitud de arco del sector.
Si el ángulo es en grados, la longitud de arco es
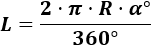
Por tanto, la longitud del arco del primer sector es
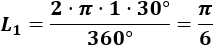
Así que el perímetro del primer sector circular es
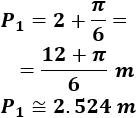
Si el ángulo es en radianes, la longitud de arco es
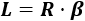
Por tanto, la longitud del arco del segundo sector es
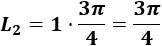
Así que el perímetro del segundo sector circular es
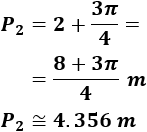
Problema 3
Calcular en grados y en radianes el ángulo del sector circular con área igual a \(6\pi cm^2\) de un circulo cuyo perímetro es \(4\pi \sqrt{2}\cdot cm\).
Ver solución
Calculamos el radio del círculo a partir de su perímetro (\(P= 2\pi R\)):
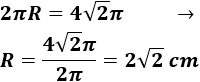
Vamos a utilizar la fórmula del área de un sector circular con el ángulo expresado en radianes:
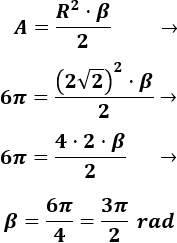
El ángulo del sector es \(3\pi /2 rad\). En grados, el ángulo es \(270^\circ\).
Problema 4
Demostrar la fórmula (con ángulo en grados) del área del sector circular a partir de la fórmula del área de un círculo (\(\pi R^2\)).
Ver solución
El área de un círculo de radio \(R\) es \(\pi\cdot R^2\). Si consideramos el círculo como un sector circular, entonces su ángulo es \(360^\circ\).
Aplicamos una regla de tres: El área del sector circular con ángulo de \(360^\circ\) es \(\pi \cdot R^2\). Entonces, el área del sector circular con ángulo \(\alpha ^\circ\) es
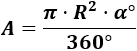
Problema 5
Demostrar la fórmula del área del sector circular con ángulo en radianes (utilizar la fórmula del Problema 4):
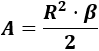
Ver solución
Podemos razonar como en el problema anterior, pero lo que haremos es pasar de grados a radianes la fórmula de problema anterior:
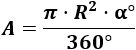
Como \(\pi\) radianes son 180°, aplicando una regla de tres, el ángulo \(\alpha^\circ\) es
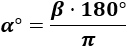
Sustituimos en la formula del problema anterior: