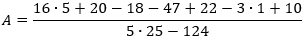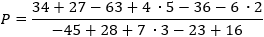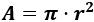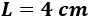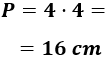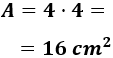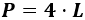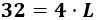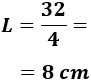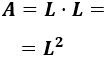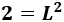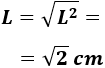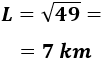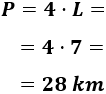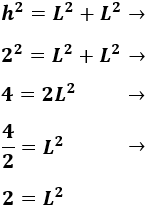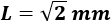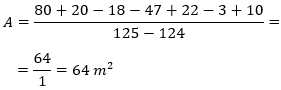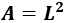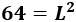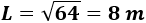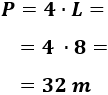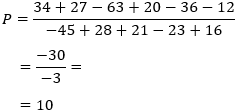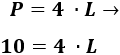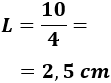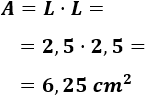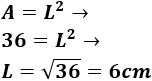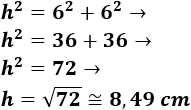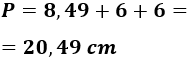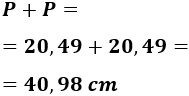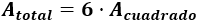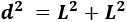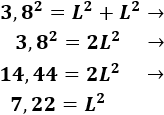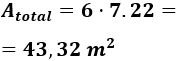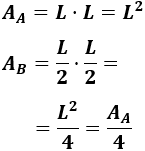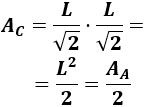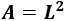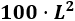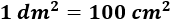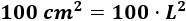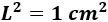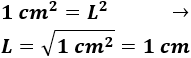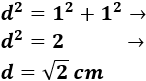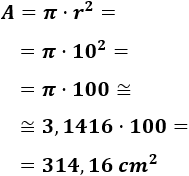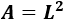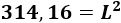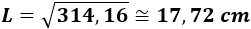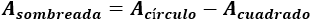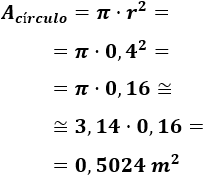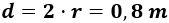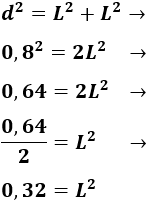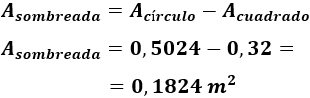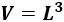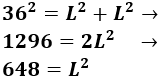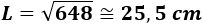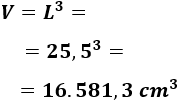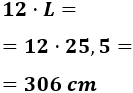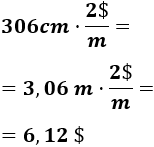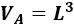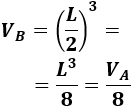Problemas sobre cuadrados
|
Contenido de esta página:
-
Ficha descriptiva del cuadrado.
-
15 Problemas resueltos ordenados de
menor a mayor dificultad.
1. Ficha descriptiva:
2. Problemas resueltos
Problema 1
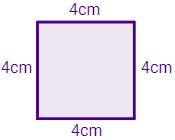
Calcular el perímetro y el área de un cuadrado de lado 4 centímetros.
Ver solución
El lado del cuadrado es
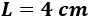
El perímetro del cuadrado es la suma de las longitudes de sus cuatro lados:
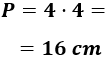
Nota: la unidad de medida del perímetro es centímetros puesto que es una longitud.
El área de un cuadrado o de un rectángulo es la base por la altura. En un cuadrado, la base y la altura son iguales.
El área del cuadrado de lado 4cm es
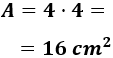
Nota: la unidad de medida del área es centímetros al cuadrado puesto que es una medida de la superficie.
¡Observad que el valor numérico del perímetro y del área coinciden, pero las unidades de medida difieren!
Problema 2

Si el perímetro de un cuadrado es 32 metros, ¿cuánto miden sus lados?
Ver solución
Todos los lados del cuadrado miden lo mismo: \(L\).
El perímetro del cuadrado es cuatro veces el lado:
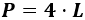
Como sabemos que el perímetro es 32 metros, tenemos la ecuación
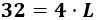
La resolvemos:
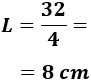
Por tanto, los lados del cuadrado miden 8 centímetros.
Problema 3
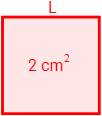
Si el área de un cuadrado es \(2cm^2\), ¿cuánto mide su lado?
Ver solución
Si los lados del cuadrado miden \(L\), entonces el área de dicho cuadrado es
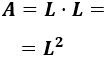
Como el área es 2, tenemos la ecuación
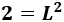
Para calcular \(L\) tenemos que hacer la raíz cuadrada:
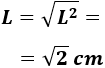
Por tanto, el lado del cuadrado mide \(\sqrt{2} cm\).
Problema 4
Si el área de un campo de fútbol gigante con forma de cuadrado es \(49km^2\), ¿cuál es la longitud total de las vallas que rodean al campo?
Ver solución
Al igual que en el problema anterior, calculamos el lado \(L\) del cuadrado a partir del área:
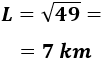
La longitud total de las vallas coincide con el perímetro del cuadrado. Calculamos el perímetro:
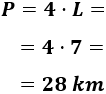
Por tanto, la longitud total de las vallas del campo es de 28 kilómetros.
Problema 5
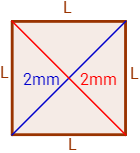
Si las diagonales de un cuadrado miden 2 milímetros cada una, ¿cuánto miden sus lados?
Ver solución
Las dos diagonales de un cuadrado miden los mismo, así que trabajamos con una de ella.
Representamos el cuadrado de lado \(L\) con una de sus diagonales:
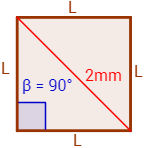
Obsérvese que la diagonal divide al cuadrado en dos triángulos rectángulos (con un ángulo recto) iguales.
Nos centramos en uno de los dos triángulos rectángulos para aplicar el teorema de Pitágoras.
Los dos catetos del triángulo miden \(L\) y su hipotenusa es la diagonal que mide 2 mm.
Por tanto,
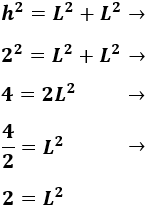
Para calcular \(L\) tenemos que hacer la raíz cuadrada:
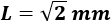
Por tanto, los lados del cuadrado miden \(\sqrt{2}\) milímetros.
Problema 6
El área en metros cuadrados de un cuadrado es
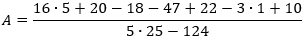
¿Cuál es el perímetro del cuadrado?
Ver solución
Sólo conocemos el área del cuadrado, pero tenemos que simplificar su expresión:
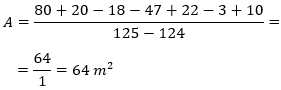
Para calcular el perímetro necesitamos calcular los lados \(L\). La fórmula del área del cuadrado es
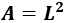
Por tanto, tenemos
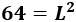
Hacemos la raíz cuadrada:
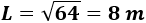
Para finalizar, sustituimos el lado \(L\) en la fórmula del perímetro:
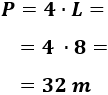
Por tanto, el perímetro del cuadrado es de 32 metros.
Problema 7
El perímetro de un cuadrado en centímetros está dado por la siguiente operación:
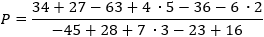
Calcular el área del cuadrado.
Ver solución
Calculamos el perímetro simplificando las operaciones:
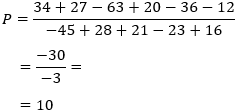
Nota: el resultado de dividir dos números negativos es un número positivo (regla de los signos).
Por tanto, el perímetro del cuadrado es 10 centímetros.
Para calcular el área, necesitamos calcular el lado \(L\). El lado podemos obtenerlo sabiendo el perímetro:
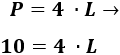
Resolvemos la ecuación:
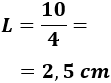
Luego el lado mide 2,5 centímetros.
Por último, calculamos el área:
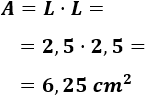
El área del cuadrado es 6,25 centímetros cuadrados.
Problema 8
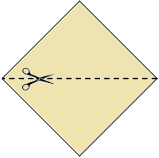
Se tiene una cartulina cuadrada cuya área es igual a \(36 cm^2\). Si se corta la cartulina por una de sus diagonales, ¿cuánto vale la suma de los perímetros de los dos triángulos que se obtienen?
Ver solución
Ya hemos dicho anteriormente que la diagonal de un cuadrado lo divide en dos triángulos rectángulos iguales. La hipotenusa del triángulo es la diagonal del cuadrado y sus catetos son los lados.
Calculamos el lado \(L\) del cuadrado a partir de su área:
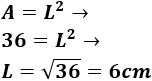
Por tanto, los catetos del triángulo miden 6cm cada uno.
Aplicamos el teorema de Pitágoras para calcular la hipotenusa \(h\) del triángulo rectángulo:
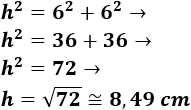
Por tanto, la hipotenusa mide aproximadamente 8,49 centímetros.
El perímetro del triángulo es
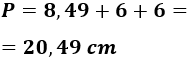
Como los triángulos son iguales, la suma de sus perímetros es
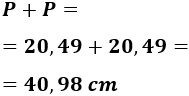
Problema 9
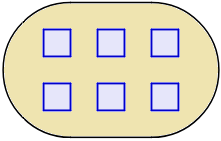
En un centro comercial hay 6 fuentes de agua iguales con forma cuadrada. Sabiendo que la diagonal de las fuentes mide 3,8 metros, calcular la superficie total de agua del centro comercial.
Ver solución
El problema nos pide la suma de las áreas de todas las fuentes, pero como son iguales, calculamos el área de una y multiplicamos por 6:
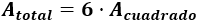
Por lo visto en los problemas anteriores, la diagonal de un cuadrado de lado \(L\) es
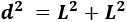
(fórmula obtenida al aplicar Pitágoras).
Por tanto,
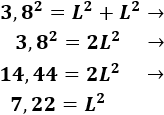
Obsérvese que ya hemos calculado el área de una de las fuentes (el área es \(A=L^2\)).
Por tanto, la superficie de agua del centro comercial es 43,32 metros cuadrados ya que
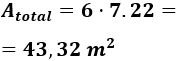
Problema 10
Se tienen dos cuadrados: el cuadrado A y el cuadrado B:
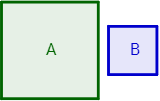
Si el lado del cuadrado B mide la mitad del lado del cuadrado A, ¿el área del cuadrado B es la mitad del área del cuadrado A?
Ver solución
No, el área del cuadrado B es la cuarta parte del área del cuadrado A.
Si el lado de A mide \(L\), el lado de B mide \(L/2\). Por tanto, sus áreas son
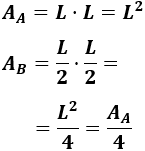
El cuadrado C cuya área es la mitad del cuadrado A es el de lado \(L/\sqrt{2}\):
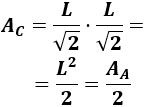
Problema 11

Si una hoja cuadriculada de \(1 dm^2\) de superficie está formada por 100 cuadrados iguales. ¿Cuánto miden las diagonales de los cuadrados?
Ver solución
La superficie de la hoja es la suma de las áreas de los 100 cuadrados. Como son iguales, todos tienen la misma área. Por tanto, la superficie de la hoja es el área de uno de los cuadrados multiplicada por 100.
Si el lado de los cuadrados es \(L\), su área es
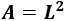
Así, la superficie de la hoja es
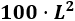
Sabemos que el área de la hoja es \(1 dm^2\). Para evitar decimales, lo escribimos en centímetros cuadrados:
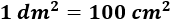
Tenemos la ecuación
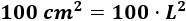
Por tanto, el área de cada cuadrado es
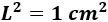
Como sabemos el área del cuadrado, podemos calcular su lado:
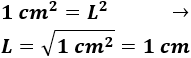
Finalmente, para calcular la diagonal \(d\) del cuadrado aplicamos Pitágoras:
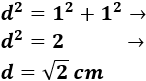
Por tanto, las diagonales de los cuadrados de la hoja miden \(\sqrt{2}\) centímetros.
Problema 12
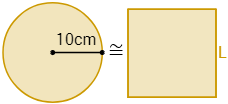
Se desea cocinar una pizza con forma cuadrada de modo que tenga aproximadamente la misma superficie que una pizza circular de radio 10cm. ¿Cuánto deben medir los lados de la pizza cuadrada?
Ayuda: el área de un círculo de radio \(r\) es \(\pi\cdot r^2\).
Ver solución
Primero calculamos el área de la pizza circular para saber qué área debe tener la pizza cuadrada.
Como el radio de la pizza es \( r = 10 cm\), aplicando la fórmula, su área es
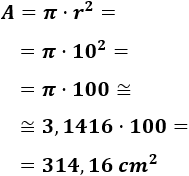
Luego la pizza circular tiene un área aproximada de 314,16 centímetros cuadrados.
La fórmula del área de un cuadrado de lado \(L\) es
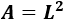
Igualamos el área a 314,16 para obtener una ecuación:
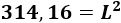
Hacemos la raíz cuadrada para obtener el lado:
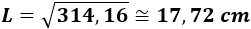
Por tanto, los lados de la pizza cuadrada deben medir aproximadamente 17,72 centímetros.
Problema 13
Un arquitecto que está trazando los planos de una casa quiere diseñar una chimenea de forma cuadrada en un espacio circular. Desde arriba la chimenea se vería así:
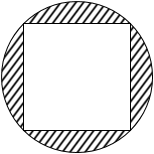
Si sabemos que el radio del área circular es de 0,4 metros, ¿cuál es el área del espacio que queda libre (espacio sombreado)?
Ayuda: el diámetro de la circunferencia coincide con la diagonal del cuadrado y el área de un círculo de radio \(r\) es
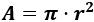
Ver solución
Como queremos calcular el área de la superficie sombreada, tenemos que restar el área del cuadrado al área del círculo:
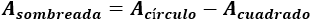
El área del círculo de radio \( r = 0,4 m\) es
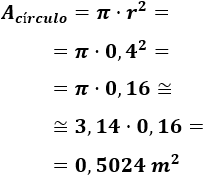
Para calcular el área del cuadrado necesitamos saber cuánto mide su lado \(L\).
Sabemos que su diagonal coincide con el diámetro de la circunferencia, es decir, su diagonal mide
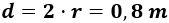
Ya sabemos que podemos calcular el lado \(L\) del cuadrado a partir de su diagonal aplicando Pitágoras:
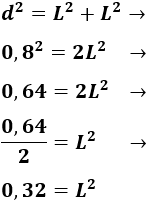
No es necesario calcular el lado ya que el área del cuadrado es \(L^2\) y ya tenemos que \(L^2 = 0,32\ m^2\).
Para terminar, restamos las áreas:
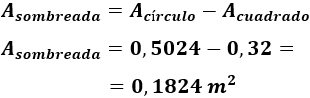
Por tanto, el área sombreada es de 0,1824 metros cuadrados. Es decir, 18,24 decímetros cuadrados.
Problema 14
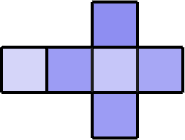
Martín dispone de 6 planchas cuadradas de metal iguales y quiere construir con ellas un cubo. El único dato que sabe Martín es que la diagonal de los cuadrados mide 36 cm. Para unir los cuadrados soldará los lados de las planchas. Si el metro de soldadura cuesta 2 dólares, calcular el volumen del cubo y el coste total de la soldadura.
Ver solución
El volumen de un cubo de lado \(L\) es
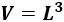
Necesitamos calcular el lado \(L\). Para obtenerlo, aplicamos Pitágoras sabiendo que su diagonal mide 36cm:
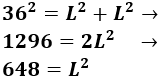
Hacemos la raíz cuadrada:
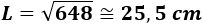
Luego el volumen del cubo es
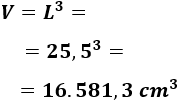
Nota: no olvidemos que las unidades de volumen son al cubo.
Para calcular cuánta soldadura necesitamos vamos a observar la siguiente imagen donde representamos los 6 cuadrados que debemos unir:

El cubo tendrá 4 uniones tanto en la base de arriba como en la base de abajo y tendrá 4 uniones más que unirían los laterales del cubo. En total, debemos soldar 12 lados.
Por tanto, se necesitan \(12\cdot L cm\) de soldadura. Es decir, se necesitan 306cm de soldadura:
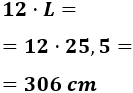
Como el precio es de 2$ por metro, el precio total es de
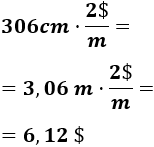
Nota: hemos pasado la longitud de centímetros a metros porque el coste de la soldadura es por metro.
Por tanto, el coste total de la soldadura del cubo es de 6,12 dólares.
Problema 15
En el problema 10 vimos que si el lado de un cuadrado B mide la mitad del lado del cuadrado A, entonces el área del cuadrado B es una cuarta parte del área del cuadrado A.
Si se tiene un cubo A de lado \(L\) y un cubo B de lado \(L/2\), ¿qué relación existe entre sus volúmenes?
Ver solución
El volumen del cubo A de lado \(L\) es
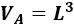
El volumen del cubo B es de lado \(L/2\) es
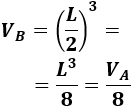
El volumen del cubo B es la octava pare del volumen del cubo A.
Por tanto, si el lado de un cubo B es la mitad del lado de un cubo A, entonces el volumen de B es la octava parte del volumen de B.

Problemas sobre Cuadrados -
(c) -
matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.