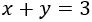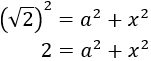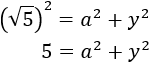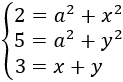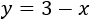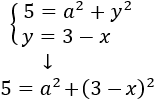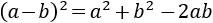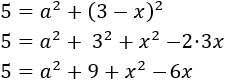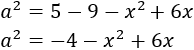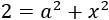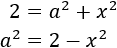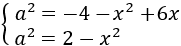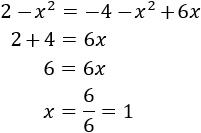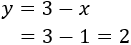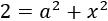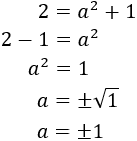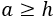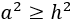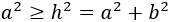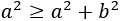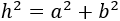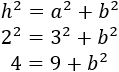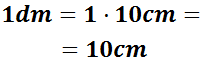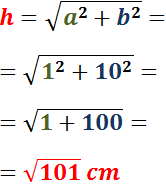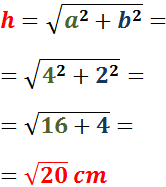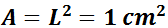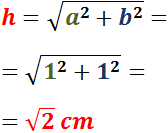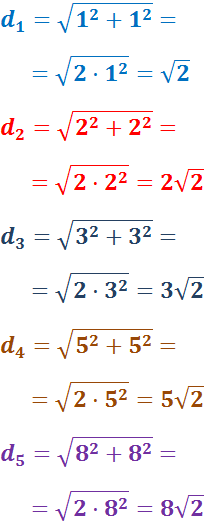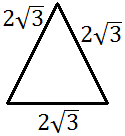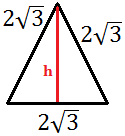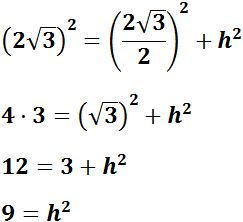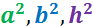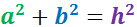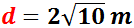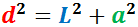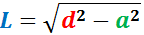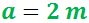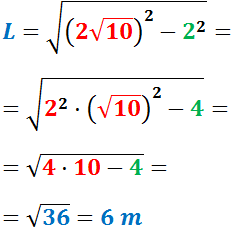Problema introductorio 
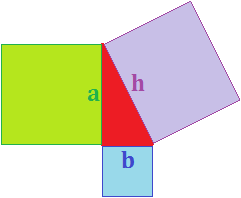
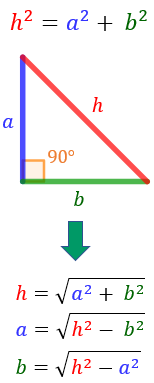
Para poder aplicar el teorema de Pitágoras es importante distinguir la hipotenusa de los catetos. Señalad la hipotenusa de los siguientes triángulos:
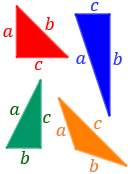
Resolvemos:
-
En el rojo, la hipotenusa es \(b\).
-
En el azul, la hipotenusa es \(a\).
-
En el verde, la hipotenusa es \(a\).
-
En el naranja no podemos hablar de hipotenusa y catetos porque no se trata de un triángulo rectángulo (es un triángulo obtusángulo).
Problema 1 
-
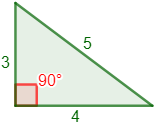
Calcular la hipotenusa del triángulo rectángulo cuyos catetos miden 3 y 4 centímetros.
-
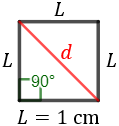
Calcular la hipotenusa del triángulo rectángulo cuyos catetos miden 1 centímetro.
Resolvemos:
Apartado 1: sabemos la medida de los catetos (\(a\) y \(b\)):
$$ a = 3 \text{ cm,} \, b = 4\text{ cm} $$
Aplicando el teorema de Pitágoras podemos calcular la hipotenusa:
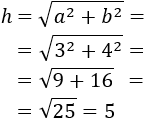
Por tanto, la hipotenusa mide 5 centímetros. Representación del triángulo:
Contenido de esta página en versión Kindle:
Apartado 2: sabemos la medida de los catetos (\(a\) y \(b\)):
$$ a = b = 1 \text{ cm} $$
Aplicamos Pitágoras:
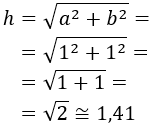
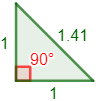
Por tanto, la hipotenusa mide \(\sqrt{2}\) centímetros o, aproximando, 1.41 centímetros. Representación del triángulo:
Problema 2 
Si la hipotenusa de un triángulo rectángulo mide 2cm y
uno de sus lados mide 1cm, ¿cuánto mide el otro lado?
Resolvemos:
Llamamos a los catetos \(a\) y \(b\) y a la hipotenusa \(h\). Luego los datos que tenemos son:
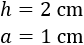
Por Pitágoras, sabemos que tiene que cumplirse
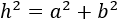
Sustituimos los valores de \(a=1\) y \(h = 2\) en la fórmula:
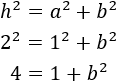
Ahora, despejamos la \(b^2\) en la ecuación:
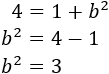
Tenemos la \(b\) al cuadrado, para calcularla, hacemos la raíz cuadrada:
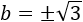
Nota: hemos escrito los signos positivo y negativo porque es lo que matemáticamente debemos hacer, pero como \(b\) representa la longitud de un
cateto, no puede ser un número negativo. Por tanto, el cateto mide
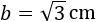
Podemos dejar la raíz cuadrada o aproximarla:
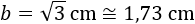
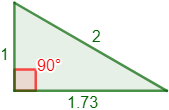
Representación del triángulo:
Problema 3 
Calcular la hipotenusa del triángulo rectángulo cuyos catetos miden 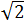 y
y 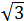 .
.
Resolvemos:
Llamamos a los catetos \(a\) y \(b\) y a la hipotenusa \(h\)
(aunque no importan los nombres siempre que apliquemos bien la fórmula del teorema).
Los datos que tenemos son
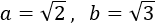
Por el teorema de Pitágoras, sabemos que la hipotenusa es
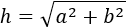
Sustituimos en la fórmula los valores conocidos (\(a\) y \(b\)):
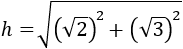
Tenemos que calcular los cuadrados de las raíces cuadradas. Recordamos que el cuadrado de una raíz cuadrada es su radicando (lo de dentro de la raíz):
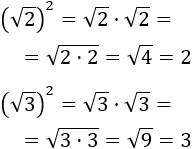
Nota: observad que hemos usado la propiedad del producto de las raíces.
Por tanto, la hipotenusa es
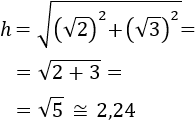
La hipotenusa mide aproximadamente 2,24. No indicamos la unidad de medida
(mm, cm, dm, m…) ya que no se indica en el enunciado.
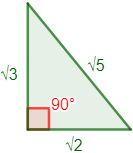
Representación del triángulo:
Problema 4 
En un campo de fútbol se han izado una bandera de España y una de México en unos mástiles de 25 metros de altura. Los mástiles se sujetan con dos cables que parten del mismo punto del suelo situado a 11 y 20 metros de distancia de los mástiles hasta cada uno de los extremos de los mismos. Calcular la longitud de ambos cables.
Resolvemos:
Representamos los triángulos rectángulos y las medidas que conocemos:
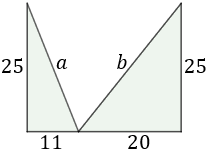
Tenemos que aplicar el teorema de Pitágoras dos veces, sin confundir que hemos llamado a y b a las hipotenusas (no son los catetos).
Calculamos la longitud del cable que sujeta la bandera de España:
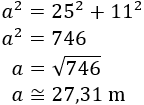
Calculamos la longitud del cable que sujeta la bandera de México:
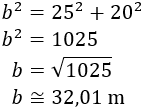
Problema 5 
-
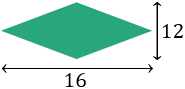
Calcular el perímetro del siguiente rombo si sabemos
que sus diagonales (altura y anchura) miden 16 y 12:
-
Calcular la altura \(h\) del triángulo isósceles cuya base mide 10 y cuyos lados miden 13:
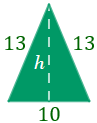
Resolvemos:
Apartado a
En primer lugar, recordad que el perímetro es la suma de todos los lados del polígono y que todos los lados de un rombo miden lo mismo.
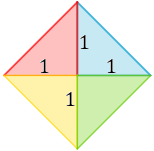
Podemos dividir el rombo en cuatro triángulos rectángulos iguales (determinados por las diagonales del rombo):
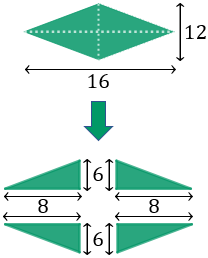
Recordad que en los rombos todos los lados miden lo mismo y los ángulos interiores son iguales dos a dos. Además, como hemos realizado una división simétrica, sabemos que
los catetos miden 8 y 6 en cada triángulo.
Observad que los lados del rombo son las hipotenusas de los 4 triángulos rectángulos. Como los triángulos son iguales, sólo hay que calcular una hipotenusa.
Para calcular la hipotenusa aplicamos el teorema de Pitágoras:
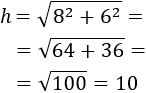
Por tanto, cada lado del rombo (o sea, cada hipotenusa) mide 10.
El perímetro es la suma de todos los lados.
Como éstos son iguales, sólo tenemos que multiplicar por 4:
Perímetro = 4·10 = 40
Apartado b
Es muy fácil ver que la altura \(h\) del triángulo lo divide en dos triángulos rectángulos de catetos \(5\) y \(h\) e hipotenusa 13. Por tanto, aplicando Pitágoras, la altura del triángulo isósceles es 12:
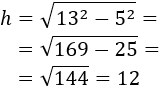
Nota: ha sido premeditado llamar \(h\) a la altura (por el inglés, height), pero no hay que confundirla con la \(h\) de hipotenusa al aplicar el teorema. Por eso en el radicando hay una resta: cuadrado de la hipotenusa menos cuadrado del cateto conocido.
Problema 6 
Calcular la altura que podemos alcanzar con una escalera de 3 metros
apoyada sobre la pared si la parte inferior la situamos a 70 centímetros de ésta.
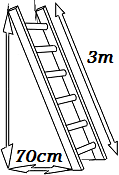
Resolvemos:
Hay que tener en cuenta que las unidades de medida no son las
mismas. Podemos escribirlas todas en metros, así 70 centímetros son 0.7 metros:
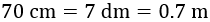
El triángulo que tenemos es
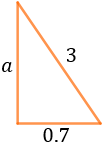
La altura es uno de los catetos (\(a\)). Aplicamos el teorema de Pitágoras para calcularla:
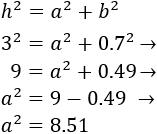
Por tanto, haciendo la raíz cuadrada,
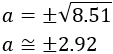
Pero como \(a\) es la altura, debe ser positiva. Por tanto, la altura será, aproximadamente 2.92 metros:
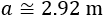
Problema 7 
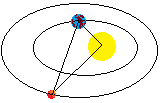
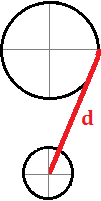
Supongamos que la Tierra (azul), Marte (rojo) y el Sol (amarillo) se encuentran por un momento formando un triángulo rectángulo. Calcular la distancia entre la Tierra y Marte sabiendo que:
-
La distancia Tierra-Sol es 150 millones de kilómetros.
-
La distancia Marte-Sol es de 225 millones de kilómetros.
Resolvemos:
La distancia buscada es la hipotenusa \(h\). Aplicamos Pitágoras:
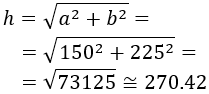
Por tanto, la distancia entre la Tierra y Marte sería de unos 270.42 millones de kilómetros.
Problema 8 
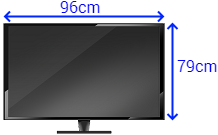
La medida que se utiliza en los televisores es la longitud de la diagonal de la pantalla en unidades de pulgadas. Una pulgada equivale a 2,54 centímetros:
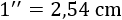
Si David desea comprar un televisor para colocarlo en un hueco de 96x79cm, ¿de cuántas pulgadas de diagonal debe ser el televisor?
Resolvemos:
Para calcular las pulgadas que caben en el hueco, debemos calcular cuánto mide su diagonal y escribir el resultado en pulgadas.
Como la diagonal del hueco es la hipotenusa de un triángulo rectángulo, aplicamos el teorema de Pitágoras:
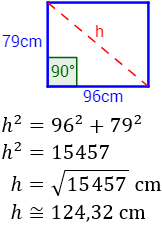
Por tanto, la diagonal mide unos 124,32cm.
Nota: deberíamos redondear la raíz cuadrada a la baja para que el televisor quepa en el hueco.
Pasamos de centímetros a pulgadas aplicando una regla de tres:
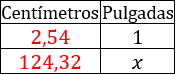
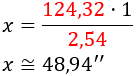
Por tanto, el televisor que debe comprar David no puede exceder las 48,94 pulgadas.
Problema 9 
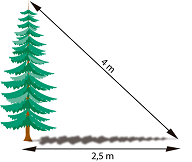
Al atardecer, un árbol proyecta una sombra de 2,5 metros de longitud. Si la distancia desde la parte más alta del árbol al extremo más alejado de la sombra es de 4 metros, ¿cuál es la altura del árbol?
Resolvemos:
Imaginamos un triángulo rectángulo de modo que
- su base, \(b\), es la sombra del árbol,
- su altura, \(a\), es la altura del árbol y
- su hipotenusa, \(h\), es la distancia desde el árbol al extremo de la sombra.
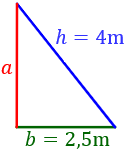
Como el triángulo es rectángulo, aplicamos el teorema de Pitágoras para calcular su altura, \(a\):
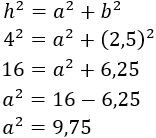
Finalmente, hacemos la raíz cuadrada:
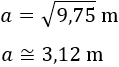
Por tanto, la altura del árbol es, aproximadamente, 3,12 metros.
Problema 10 
Un clavadista (saltador de trampolín) está entrenando en una piscina con una plataforma. Cuando realiza el salto, cae a una distancia de 1 metro de la plataforma sumergiéndose 2,4 metros bajo el agua. Para salir a la superficie, bucea hasta el final de la piscina siguiendo una línea transversal de 8,8 metros de longitud.
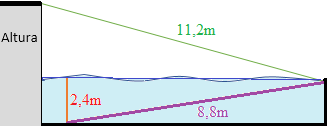
Si la longitud desde la parte superior de la plataforma al lugar en donde emerge del agua es de 11,2 metros, ¿cuál es la altura de la plataforma (desde el nivel del agua)?
Resolvemos:
Según la representación, la profundidad de la piscina es de 2,4 metros.
Tenemos un rectángulo de altura 2,4 m y cuya diagonal mide 8,8 m. Dicho de otro modo, tenemos un triángulo rectángulo cuya hipotenusa mide 8,8 m y uno de sus catetos mide 2,4 m. Calculamos el otro cateto b por Pitágoras (es la base del rectángulo):
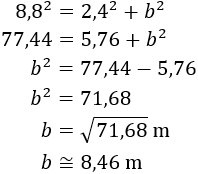
Pero como el clavadista cae a 1 metro de la plataforma, la longitud de la piscina es de 9,46 metros.
Para calcular la altura \(a\) de la plataforma nos ayudamos del triángulo rectángulo cuya hipotenusa mide 11,2m y cuya base mide 9,46m:
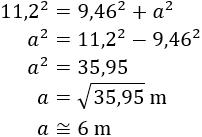
Por tanto, la altura de la plataforma es de unos 6 metros por encima del nivel del agua.
Problema 11 
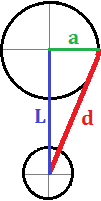
Un parque de diversiones quiere construir una nueva atracción que consiste en una tirolesa que parte desde la base superior de una columna con forma cilíndrica. Si el radio de la columna es \(R = 2\) metros y el área de su lateral es de 120π metros cuadrados, calcular la longitud del cable de la tirolesa para que alcance el suelo a 40 metros de distancia de la columna.
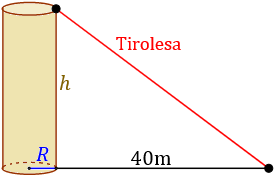
Resolvemos:
Tenemos un triángulo rectángulo de base 40m cuya hipotenusa coincide con la tirolesa. La altura de la columna, \(h\), la podemos calcular a partir de su área lateral y su radio, \(R\).
El área lateral del cilindro es la del rectángulo de altura \(h\) y cuya base es el perímetro de la base del cilindro, es decir, dos veces el radio por pi.
Por tanto, el área del lateral de la columna es
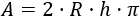
Sustituimos el área (\(A =120\pi m^2\)) y el radio (\(R=2m\)) y resolvemos la ecuación:
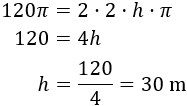
Luego la altura de la columna es de 30 metros.
Finalmente, calculamos la hipotenusa aplicando el teorema de Pitágoras:
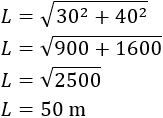
Nota: hemos llamado \(L\) a la hipotenusa para no confundirla con la altura \(h\) de la columna.
El cable de la tirolesa debe medir 50 metros de longitud.
Problema 12 
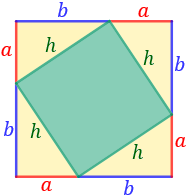
Demostrad el teorema de Pitágoras con la ayuda de la siguiente figura:
Ayuda: necesitaréis
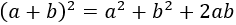
Resolvemos:
Primero, observemos la figura:
-
Está formada por 4 triángulos rectángulos iguales cuyos catetos miden \(a\) y \(b\) y la hipotenusa, \(h\).
-
El lado del cuadrado exterior es \(L = a+b\) y su área coincide con la suma del área de los triángulos y la del cuadrado interior de lado \(h\).
La fórmula que tenemos que demostrar es la del teorema de Pitágoras:
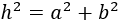
Demostración:
El lado del cuadrado exterior es
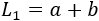
Por tanto, el área de dicho cuadrado es
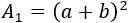
Esta área ha de coincidir con la suma de las áreas de los 4 triángulos y la del cuadrado interior. Vamos a calcular estas áreas.
Cuadrado interior:
El cuadrado interior tiene lado \(h\), así que su área es
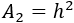
Triángulos:
Los triángulos son rectángulos y sus catetos son la altura y la base. Luego el área de cada uno de los triángulos es
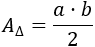
Como el área del cuadrado exterior es igual a la suma de las áreas de los otros polígonos, tenemos:
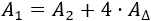
Nota: en el lado derecho hemos escrito la suma del área del cuadrado interior y 4 veces el área de uno de los triángulos.
Ahora, en la fórmula anterior sustituimos las fórmulas de área que hemos visto:
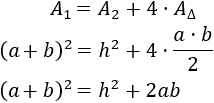
Aplicamos la fórmula del cuadrado de la suma en el lado izquierdo:
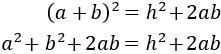
El sumando \(2ab\) aparece en ambos lados, así que lo podemos eliminar:
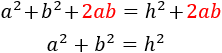
Por tanto, queda demostrado el teorema de Pitágoras:
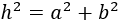
Problema 13 
- Si los dos catetos de un triángulo rectángulo miden lo mismo, ¿cuánto mide la hipotenusa? Da un ejemplo.
-
Si uno de los catetos de un triángulo rectángulo mide el doble que el otro, ¿cuánto mide la hipotenusa? Da un ejemplo.
- ¿Puede la hipotenusa de un triángulo medir exactamente lo mismo que la suma de sus catetos? Da un ejemplo o contraejemplo.
Resolvemos:
En los tres apartados llamaremos \(a\) y \(b\) a los catetos y \(h\) a la hipotenusa.
Apartado a
Como los catetos miden lo mismo, \(a = b\).
Por Pitágoras,
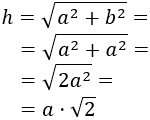
Ejemplo: si los catetos miden 1, \(a = 1\), entonces la hipotenusa mide
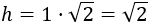
Apartado b
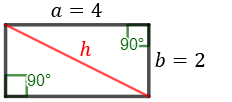
Como uno de los catetos mide el doble que el otro, \(b = 2\cdot a\).
Por Pitágoras,
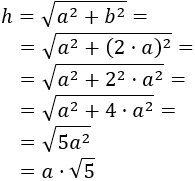
Ejemplo: si los catetos miden 1 y 2, \(a = 1\) y \(b = 2\cdot 1 = 2\), entonces la hipotenusa mide
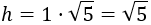
Apartado c
Debe cumplirse que la suma de los catetos es igual a la hipotenusa:
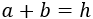
Calculamos el cuadrado de la hipotenusa:
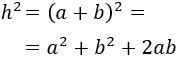
Sin embargo, por Pitágoras,
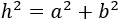
Pero entonces, como \(h^2 = h^2\), tenemos
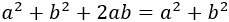
Es decir,
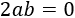
Pero esto sólo sería posible si a = 0, o bien, b = 0, lo cual es una posibilidad imposible, dado que a y b son las longitudes de los catetos.
Luego hemos demostrado por reducción al absurdo la falsedad del apartado c.
Contraejemplo: si los catetos miden 1 y la hipotenusa mide 2, no se cumpliría el teorema de Pitágoras ya que
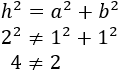
Problema 14 
Dificultad muy alta: se requiere resolver un sistema de ecuaciones no lineales.
Calcular la altura del siguiente triángulo sabiendo que sus lados miden
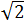 ,
,
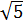 y su base 3.
y su base 3.
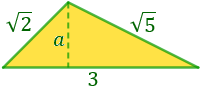
Resolvemos:
Para poder calcular la altura del triángulo, \(a\),
tenemos que dividirlo en dos triángulos rectángulos (para
poder aplicar el teorema de Pitágoras).
Los dos triángulos son los siguientes:
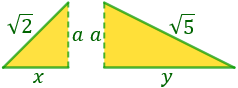
La base del triángulo (que mide 3) se divide en dos partes no iguales (la base de cada triángulo).
No sabemos cuánto mide cada base, pero sí que sabemos que las dos bases suman 3:
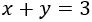
Aplicamos Pitágoras al primer triángulo y obtenemos una ecuación:
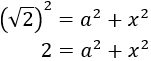
Nota: no conocemos ninguno de los dos catetos implicados (\(a\) y \(x\)).
Procediendo del mismo modo para el otro triángulo, obtenemos
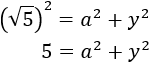
Es decir, tenemos las siguientes ecuaciones:
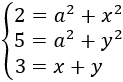
Se trata de un sistema de ecuaciones no lineales ya que algunas de las incógnitas se encuentran elevadas al cuadrado.
Podemos aislar fácilmente la \(y\) en la tercera ecuación, obteniendo
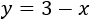
En la segunda ecuación tenemos una \(y\), que sabemos que
es \(3-x\), así que sustituimos en ella:
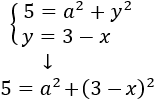
Como tenemos una resta al cuadrado, aplicamos la fórmula del binomio de
Newton (diferencia al cuadrado), que recordamos que es la siguiente:
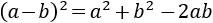
Operamos aplicando la fórmula anterior:
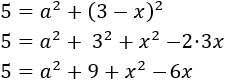
Ahora despejamos \(a^2\):
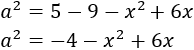
Recordemos que también teníamos la ecuación
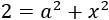
Despejamos también en ella \(a^2\):
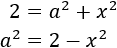
Es decir, las dos ecuaciones que tenemos son
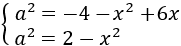
Y como \(a^2 = a^2\), podemos igualar ambas
expresiones algebraicas obteniendo una ecuación de primer grado fácil de resolver:
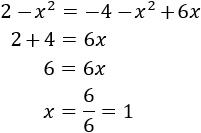
Sabiendo el valor de \(x\) podemos obtener el de \(y\):
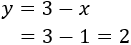
Ya sabemos cuánto mide cada base y podemos ahora calcular la altura.
La primera de las ecuaciones era
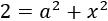
Como sabemos que \(x = 1\), podemos calcular \(a\):
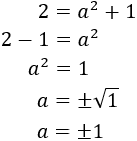
Y como \(a\) es la altura, no puede ser negativa. Por tanto, la altura del triángulo es \(a = 1\).
Problema 15 
¿Uno o ambos catetos de un triángulo rectángulo pueden medir más que la hipotenusa? Dad algún ejemplo.
Resolvemos:
La respuesta es NO, como ya hemos indicado al comienzo de la página, pero veamos por qué.
Llamaremos \(a\) y \(b\) a los catetos y \(h\) a la hipotenusa.
Supongamos que \(a\) mide más (o lo mismo) que la hipotenusa, entonces tenemos
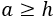
Como \(a \ge h\), sus cuadrados también cumplen esta relación:
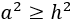
Por Pitágoras sabemos que \(h^2 = a^2 + b^2\), con lo que tenemos que
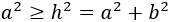
Es decir,
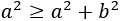
Pero esto no puede ser cierto ya que \(a^2 + b^2\) es un número mayor que \(a^2\) (porque \(b^2 > 0\)).
Hemos supuesto que \(a \ge h\) y hemos obtenido una falsedad, lo que significa que \(a \ge h\) no puede ser cierto. Por tanto, necesariamente \(a < h\).
Lo visto para \(a\) también es aplicable para \(b\):
Ninguno de los catetos puede medir lo mismo o más que lo que mide la hipotenusa.
Ejemplo: supongamos que tenemos un triángulo rectángulo cuya hipotenusa mide 2 y uno de sus catetos mide 3. Es decir, tenemos \(a = 3\) y \(h = 2\). No nos importa cuánto mide el otro cateto, \(b\).
Por Pitágoras, el cuadrado de la hipotenusa es
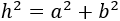
Sustituimos los datos en la ecuación:
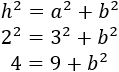
Observad que la igualdad nunca será cierta porque el lado izquierdo de la igualdad (4) es siempre menor que el derecho (que es mayor que 9).
Más problemas: Problemas de Pitágoras (PyE).



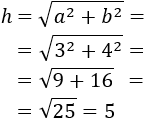

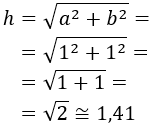

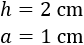
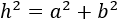
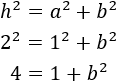
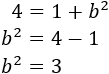
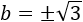
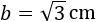
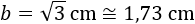

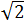 y
y 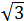 .
. 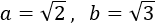
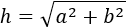
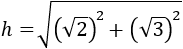
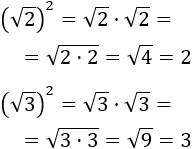
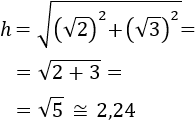



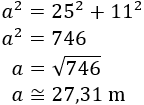
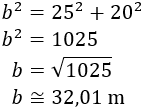



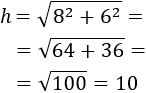
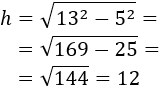

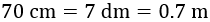

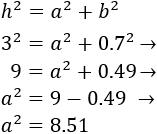
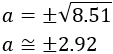
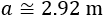

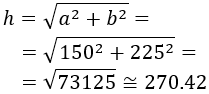

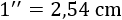


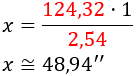


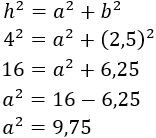
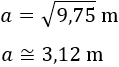


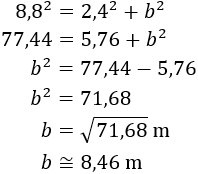

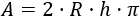
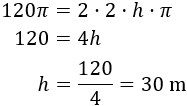
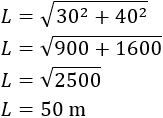

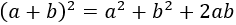
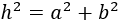
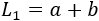
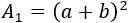
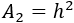
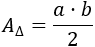
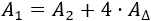
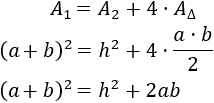
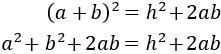
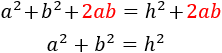

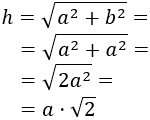
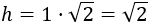
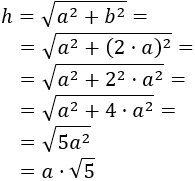
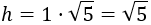
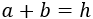
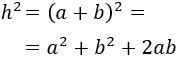
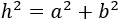
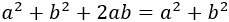
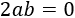
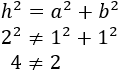
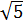 y su base 3.
y su base 3.