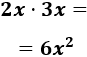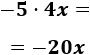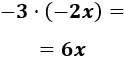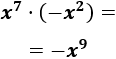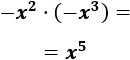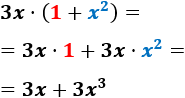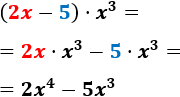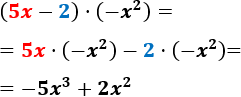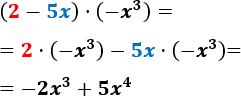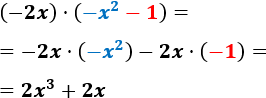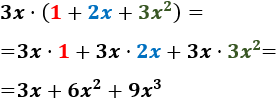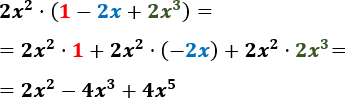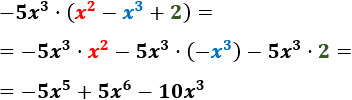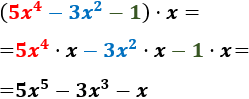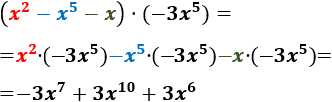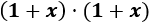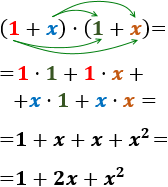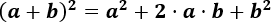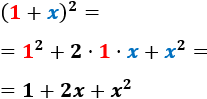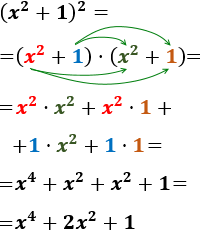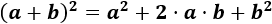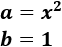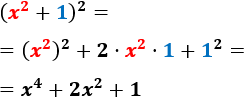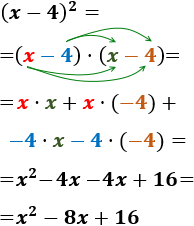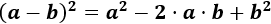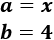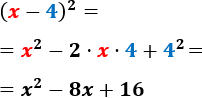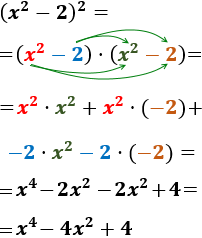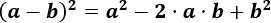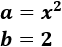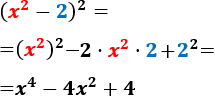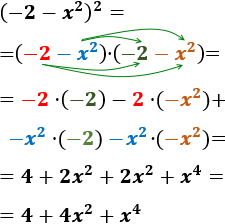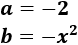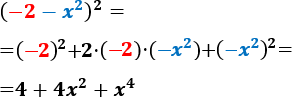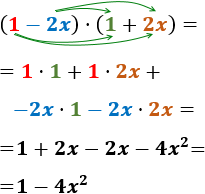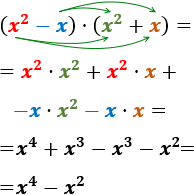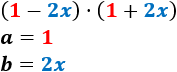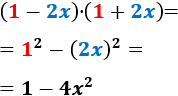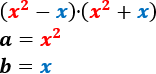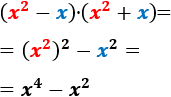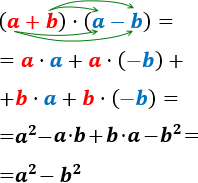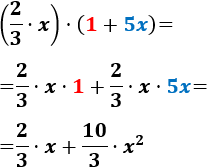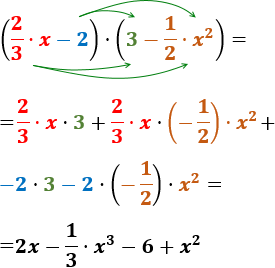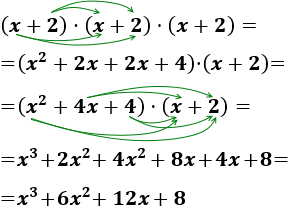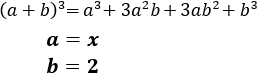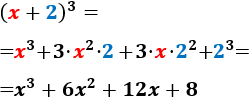Multiplicación de polinomios
Contenido de esta página:
- Introducción
- Monomios y polinomios (recordatorio)
- Grado de un polinomio (recordatorio)
- Método para multiplicar polinomios
- Grado del polinomio producto (grado del resultado)
- Productos notables: cuadrado de un binomio y suma por diferencia.
- 10 problemas resueltos: multiplicación de polinomios.
1. Introducción
En esta página vamos a ver cómo multiplicar polinomios, por ejemplo, multiplicar los polinomios \(3x+1\) y \(2-x^2\):
$$(3x+1)\cdot (2-x^2) =$$
$$=-3x^3-x^2+6x+2 $$
Después, hablaremos sobre la relación que hay entre el grado del polinomio del resultado con el grado de los polinomios del producto. También, calcularemos las fórmulas de algunos productos notables, como el cuadrado y el cubo de un binomio. Para terminar, resolveremos 10 problemas de productos de polinomios.
Nota: la parte literal de los monomios con los que trabajaremos tienen sólo potencias de \(x\).
2. Monomios y polinomios
Recordatorio de los conceptos de monomio, binomio, trinomio y polinomio.
Un monomio es el producto de un número real (un número positivo, negativo o cero) por una o varias variables literales.
Un ejemplo de monomio es \( -5x^2\), que también podemos escribir como \(-5\cdot x^2\) ó \(-5\cdot x\cdot x\).
El número del monomio (con signo) se denomina coeficiente del monomio. El resto del monomio (variables literales, es decir, las letras) se denomina parte literal del monomio.
En el monomio \(-5x^2\), el coeficiente es \(-5\) y la parte literal es \(x^2\).
- Un monomio puede no tener parte literal. Por ejemplo, el monomio \(4\) no tiene parte literal. En este caso, puede considerarse que la parte literal tiene exponente nulo: \( 4 = 4x^0\).
- Un monomio puede no tener coeficiente, por ejemplo, \(x^2\). En realidad, esto ocurre cuando el coeficiente es 1: \( x^2 = 1\cdot x^2\).
Un binomio es una expresión algebraica constituida por dos monomios. Por ejemplo, \( 3x -x^2\).
Un trinomio está constituido por tres monomios. Por ejemplo, \(2x-3x^2+x^3\).
Un polinomio está constituido por varios monomios. Por ejemplo, \(x^2-x^5-x\).
Recordad que dos monomios sólo se pueden sumar (o restar) cuando tienen la misma parte literal.
Ejemplos:
- Los monomios \(3x\) y \(5x\) se pueden sumar: $$ 3x+5x = 8x $$
- Los monomios \(3x\) y \(5x^2\) no se pueden sumar.
- Los monomios \(2x\) y \(3y\) no se pueden sumar.
3. Grado de un polinomio
Concepto de grado de un polinomio.
En esta página, la parte literal de los monomios es una potencia de \(x\). Por ejemplo, \(3x\), \(2x^2\), \(4x^5\),... En esta situación, se define el grado de un monomio como el exponente de su parte literal.
Ejemplos:
- El grado de \(3x^2\) es 2.
- El grado de \(5x\) es 1.
- El grado de \(7\) es 0 porque \(7 = 7x^0\).
El grado de un polinomio es al mayor de los grados de los monomios que lo conforman.
Ejemplos:
- El grado del binomio \(x-2x^3\) es 3.
- El grado del trinomio \(x-x^2-5\) es 2.
- El grado del polinomio \(x^2-x-3x^5+2\) es 5.
4. Método para multiplicar polinomios
El resultado de multiplicar dos polinomios es la suma del producto de todos los monomios del primer polinomio por todos los monomios del segundo polinomio.
Importante: las multiplicaciones incluyen los signos de los monomios.
Recordatorio: al multiplicar dos potencias con la misma base, los exponentes se suman. Por ejemplo,
$$ x^3 \cdot x^2 = x^{3+2} = x^5 $$
Ejemplo 1
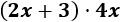
Vamos a multiplicar el binomio \(2x+3\) por el monomio \(4x\). Para ello, multiplicamos \(2x\) por \(4x\) y \(3\) por \(4x\):
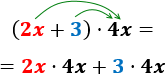
El producto \(2x\cdot 4x\) se simplifica multiplicado sus coeficientes y sumando los exponentes de sus partes literales (1 y 1):
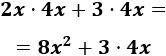
Hacemos lo mismo con el producto \(3\cdot 4x\) (ahora los exponentes son 0 y 1):
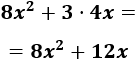
Por tanto, el producto calculado es
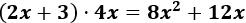
Ejemplo 2
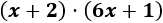
Vamos a multiplicar los binomios \(x+2\) y \(6x+1\).
Primero, multiplicamos el monomio \(x\) del primer polinomio por los dos monomios del segundo. Después, hacemos lo mismo con el segundo monomio (\(+2\)):
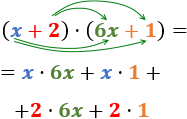
Simplificamos el resultado (multiplicando los coeficientes y sumando los exponentes de las partes literales):
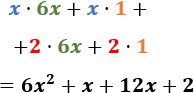
Podemos simplificar más:
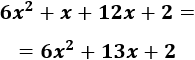
Por tanto,
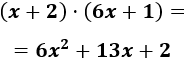
Ejemplo 3
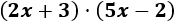
Vamos a multiplicar los binomios \(2x+3\) y \(5x-2\). ¡Cuidado con el signo negativo!
Primero, multiplicamos el monomio \(2x\) del primer polinomio por los dos monomios del segundo. Después, hacemos lo mismo con el segundo monomio (\(+3\)):
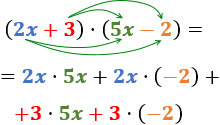
Simplificamos el resultado:
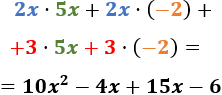
Podemos simplificar más:
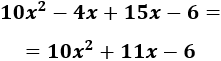
Por tanto,
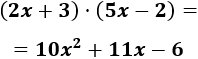
5. Grado del resultado
El grado del polinomio que se obtiene al multiplicar dos polinomios es la suma de los grados de los polinomios que se multiplican.
Ejemplos:
- El producto de un polinomio de grado 1 y de uno de grado 2 es un polinomio de grado 3. Por ejemplo,
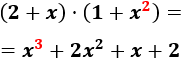
- El producto de dos polinomios de grado 2 es un polinomio de grado 4. Por ejemplo,
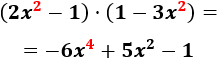
6. Productos notables
Cuadrado de un binomio (suma):
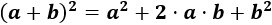
Cuadrado de un binomio (resta):
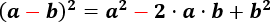
Suma por diferencia:
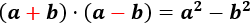
Recordad que una potencia representa el producto de un factor por sí mismo tantas veces como indica el exponente. Por ejemplo, la potencia \(2^2\) es el producto \(2\cdot 2\).
Al igual que hacemos con los números, cuando tenemos un polinomio multiplicado por sí mismo, podemos escribirlo en forma de potencia.
Ejemplos:
- Binomio al cuadrado:
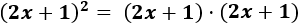
- Binomio al cubo:
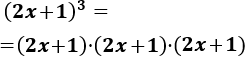
Podemos calcular estas potencias multiplicando uno a uno los monomios, pero tenemos las fórmulas anteriores para obtener el resultado más rápidamente.
Ejemplo:
Aplicamos la fórmula de la suma al cuadrado para calcular el cuadrado \((2x+1)^2\):
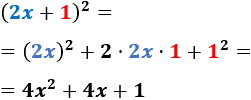
También, podemos calcular el producto sin la fórmula:
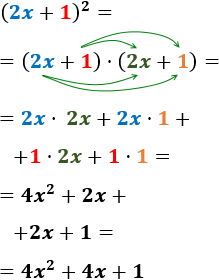
El resultado es el mismo, pero es más rápido aplicar la fórmula.
Las fórmulas de los productos notables se obtienen multiplicando los monomios uno a uno. Más información: Productos notables.
Problemas Resueltos
Problema 1 
Calcular los siguientes productos de monomios:
- \( 2x\cdot 3x\)
- \(-5\cdot 4x\)
- \( -3\cdot (-2x)\)
- \(x^7\cdot (-x^2)\)
- \(-x^2\cdot (-x^3)\)
Problema 2 
Calcular los siguientes productos de un monomio por un binomio:
- \( 3x\cdot (1+x^2)\)
- \( (2x-5)\cdot x^3\)
- \( (5x-2)\cdot (-x^2)\)
- \((2-5x)\cdot (-x^3)\)
- \( (-2x)\cdot (-x^2-1)\)
Problema 3 
Calcular los siguientes productos de un monomio por un trinomio:
- \( 3x\cdot (1+2x+3x^2)\)
- \( 2x^2 \cdot (1-2x+2x^3)\)
- \( -5x^3 \cdot (x^2-x^3+2)\)
- \( (5x^4 -3x^2-1)\cdot x\)
- \( (x^2-x^5-x)\cdot (-3x^5)\)
Problema 4 
Sin calcular el producto, ¿cuál es el grado del polinomio resultado de los siguientes productos?
- \( (2+x)\cdot (x^2-1)\)
- \( (x^2-x^4)\cdot (2x-x^2)\)
- \( (x^2-x^6+4)\cdot (5x-6x^3+2)\)
- \( (3+x^2)\cdot (x-3x^8-x^2)\)
- \( (3x^2+x^3)\cdot (x^3-2x^2)\cdot (1-x^7)\)
Problema 5 
Calcular, con o sin fórmula, los siguientes binomios al cuadrado:
- \( (1+x)^2 \)
- \( (x^2+1)^2 \)
- \( (x-4)^2 \)
- \( (x^2-2)^2 \)
- \( (-2-x^2)^2 \)
Problema 6 
Calcular los siguientes productos (suma por diferencia) sin aplicar la fórmula:
- \( (1-2x)\cdot (1+2x)\)
- \( (x^2-x)\cdot (x^2+x)\)
Problema 7 
El producto "suma por diferencia" es un producto notable cuya fórmula es
$$ (a+b)\cdot (a-b) = a^2 -b^2$$
- Calcular los productos del problema anterior aplicando la fórmula.
- Obtener la fórmula calculando el producto \((a+b)\cdot (a-b)\).
Problema 8 
Calcular el siguiente producto de polinomios con coeficientes racionales (fracciones):
$$ \left( \frac{2}{3}\cdot x \right)\cdot (1+5x) $$
Problema 9 
Calcular el siguiente producto de polinomios con coeficientes racionales (fracciones):
$$ \left( \frac{2}{3}\cdot x -2 \right)\cdot (3-\frac{1}{2}\cdot x^2 ) $$Problema 10 
Calcular el producto
$$ (x+2)\cdot (x+2)\cdot (x+2) $$
Comprobar que se obtiene el mismo resultado aplicando la fórmula del cubo de un binomio:
$$ (a+b)^3 = a^3+3a^2b + 3ab^2+b^3$$
Multiplicar polinomios - (c) - matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.