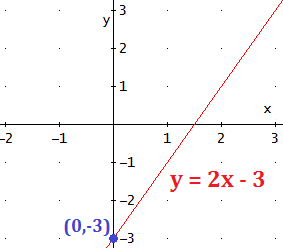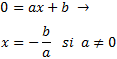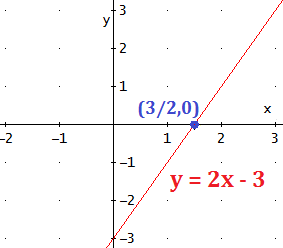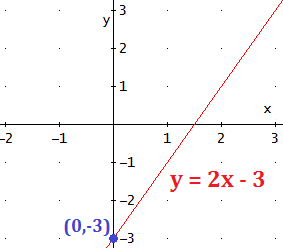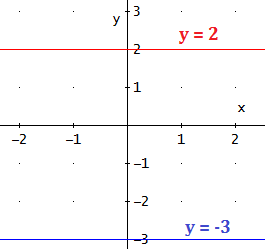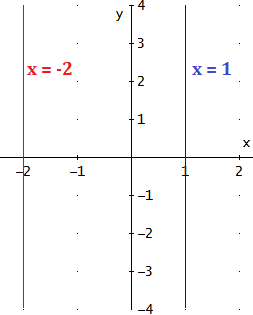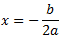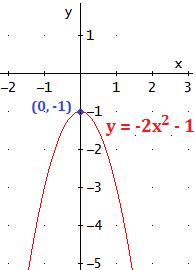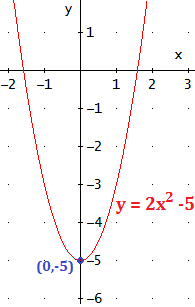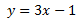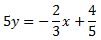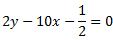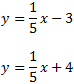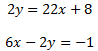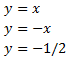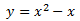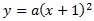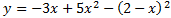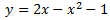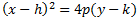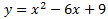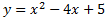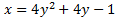Contenido de esta página:
-
Recordatorio de rectas y parábolas
-
10 problemas resueltos sobre rectas
-
10 problemas resueltos sobre parábolas
1. Rectas
La ecuación general de una recta es
$$ y = ax+b $$
Al número \(a\) se le llama pendiente y al número \(b\), término independiente u ordenada al origen.
Ejemplo: la pendiente de la recta \( y = 2x -3\) es \(a = 2\) y la ordenada es \(b = -3\).
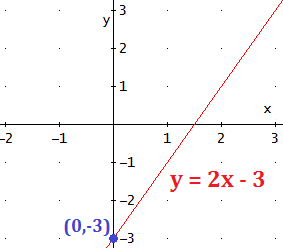
Observando su gráfica:
-
La recta es creciente (de izquierda a derecha) porque su pendiente \(a = 2\) es positiva.
-
La recta corta al eje OY en el punto \((0,-3\)) porque su ordenada es \(b = -3\).
Puntos de corte con los ejes
Con el eje OX (de abscisas)
Ocurre cuando \(y = 0\).
Para calcular el punto, resolvemos la ecuación que resulta al cambiar \(y\) por 0. Es decir, resolvemos la ecuación de primer grado
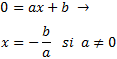
El punto de corte de la recta \(y = ax+b\) con el eje OX es \((-b/a,0)\).
Ejemplo: el punto de corte de la recta \( y = 2x -3\) con el eje OX es \((3/2,0)\):
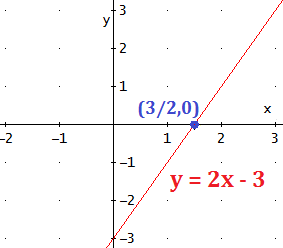
Con el eje OY (de ordenadas)
Ocurre cuando \(x = 0\).
Para calcular el punto, calculamos \(y\) sustituyendo \(x\) por 0 en la ecuación. Obtendremos la ordenada: \(y = b\).
El punto de corte de la recta \(y = ax +b\) con eje eje OY es \((0, b)\).
Ejemplo: el punto de corte con el eje OY de la recta \(y = 2x-3\) es \((0,-3)\):
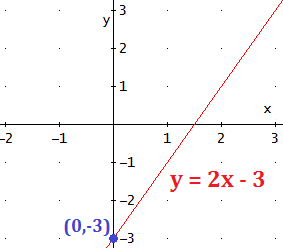
Rectas especiales
Hay dos tipos de rectas que consideramos especiales: las rectas horizontales y las rectas verticales.
Recta horizontal:
Una recta es horizontal cuando su pendiente es 0. Por tanto, su ecuación es de la forma
$$ y = b $$
La recta corta al eje OY en el punto \((0,b)\) y si \(b = 0\), entonces coincide con el eje OX.
Una recta horizontal es paralela al eje OX y, por tanto, nunca corta a dicho eje (excepto cuando \(b=0\)).
Ejemplos: las rectas \(y = 2\) e \(y = -3\) son rectas horizontales:
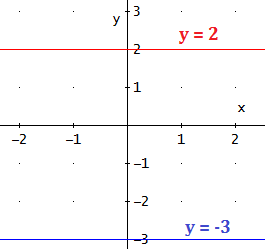
Recta vertical:
La ecuación general de una recta vertical es
$$ x = k $$
Esta recta corta el eje OX en el punto \((k,0)\) y si \(k = 0\), entonces la recta coincide con el eje OY.
Una recta vertical no tiene pendiente ni ordenada.
Nota: una recta vertical no es la gráfica de una función. Por ello, en su ecuación no aparece la \(y\).
Ejemplos: las rectas \(x = -2\) y \(x = 1\) son rectas vertivales:
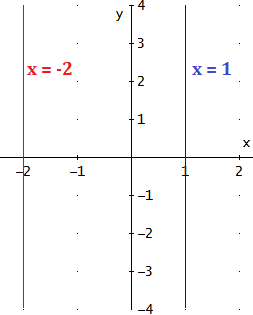
2. Parábolas
La ecuación general de una parábola es
$$ y = ax^2 + bx +c $$
Los coeficientes \(b\) y \(c\) pueden ser 0. Si \(a = 0\), es una recta y no
una parábola.
El coeficiente \(a\) se denomina coeficiente principal y el coeficiente \(b\), término independiente.
Forma de una parábola
El coeficiente \(a\) de la parábola determina su orientación.
-
Cuando \(a > 0\), la parábola tiene forma de U. Por ejemplo,
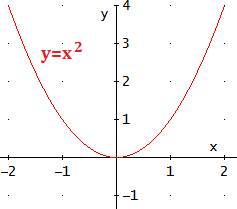
-
Cuando \(a < 0\), tiene forma de U invertida. Por ejemplo,
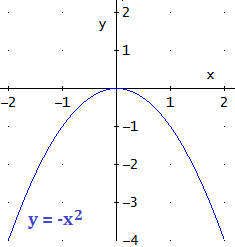
Puntos de corte con los ejes
Con el eje OX (de abscisas)
Ocurre cuando \(y = 0\).
Para calcular el punto, resolvemos la ecuación que resulta al cambiar \(y\) por 0. Es decir, resolvemos la ecuación de segundo grado
$$ 0 = ax^2 + bx + c$$
Como las ecuaciones de segundo grado pueden tener 2, 1 ó ninguna solución, una parábola puede tener 2, 1 ó ningún punto de corte con el eje OX.
Ejemplos:
-
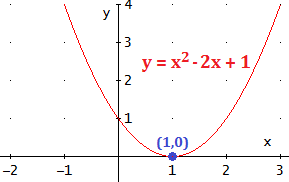
La parábola \(y = x^2 - 2x + 1\) tiene sólo un punto de corte con OX:
$$ x = \frac{2\pm \sqrt{4-4}}{2} = \frac{2\pm 0}{2}=1 $$
-
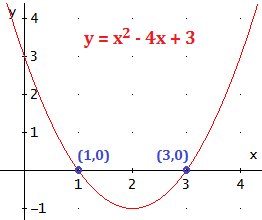
La parábola \(y = x^2 - 4x + 3\) tiene dos puntos de corte con OX:
$$ x = \frac{4\pm \sqrt{16-12}}{2} = \frac{4\pm 2}{2} = 3, \ 1 $$
-
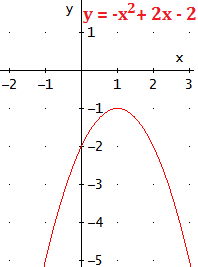
La parábola \(y = - x^2 + 2x - 2\) no tiene puntos de corte con OX:
$$ x = \frac{-2\pm \sqrt{4-8}}{-2} = \frac{-2\pm \sqrt{-4}}{-2} $$
Con el eje OY (de ordenadas)
Ocurre cuando \(x = 0\).
Para calcular el punto, calculamos \(y\) sustituyendo \(x\) por 0 en la ecuación. Obtendremos \(x = c\) y, por tanto, el punto de corte con OY es \((0,c)\).
Vértice de una parábola
El vértice de una parábola está en el punto cuya primera coordenada es
$$ x = \frac{-b}{2a}$$
El vértice de una parábola es su punto máximo o mínimo (uno de los dos).
Si la parábola tiene forma de U, el vértice es un mínimo. Si tiene forma de U invertida, es un máximo.
El vértice está en el punto cuya primera coordenada es
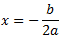
Para saber la coordenada \(y\) tenemos que substituir en la ecuación el valor de \(x\).
Ejemplos:
3. Problemas sobre rectas
Problema 1
Calcular los puntos de corte de los ejes con la recta
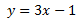
¿Cuál es la pendiente y la ordenada de la recta?
¿El punto A(1, 2) es un punto de la recta?
Solución
La pendiente es el coeficiente de la \( x\), es decir, \(a = 3\). La ordenada es el término independiente, es decir, \(b = -1\).
Como la pendiente es positiva, la recta es creciente (de izquierda a derecha).
Puntos de corte con el eje OY:
La recta corta al eje OY cuando \( x = 0\). Sustituimos
en la ecuación:
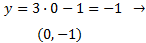
El punto de corte es \((0,-1)\).
Puntos de corte con el eje OX:
Ocurre cuando \( y = 0\). Sustituimos en la ecuación:
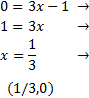
El punto de corte es \((1/3,0)\).
Sabiendo los puntos de corte, podemos representar la recta fácilmente.
La gráfica es
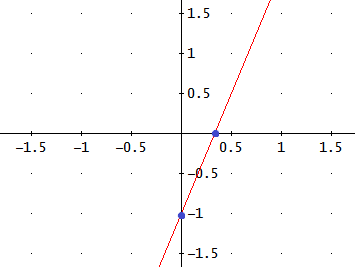
Si el punto A(1,2) está en la recta, entonces sus coordenadas deben cumplir la ecuación.
La primera coordenada del punto A es \(x=1\) y la segunda es \(y = 2\). Sustituimos en la ecuación:
$$ y = 3x-1$$
$$ 2 = 3\cdot 1 -1$$
$$ 2 = 2$$
Como se verifica la ecuación, el punto A(1,2) sí está en la recta.
Problema 2
Calcular los puntos de corte de los ejes con la recta
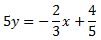
¿Cuál es la pendiente y la ordenada de la recta?
¿El punto A(1, 2) es un punto de la recta?
Solución
Como la \(y\) está multiplicada por 5, dividimos toda la ecuación entre 5 para obtener la ecuación general de la recta (forma \(y = ax+b\)):
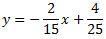
Por tanto, la pendiente es \(a = -2/15\) y la ordenada es \(b = 4/25\). Como la pendiente es negativa, la recta es decreciente.
Puntos de corte con el eje OY:
Ocurre cuando \( x = 0\). Sustituimos en la ecuación:
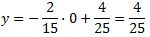
El punto es \((0, 4/25)\).
Puntos de corte con el eje OX:
Es el punto con \(y=0\). Sustituimos en la ecuación:
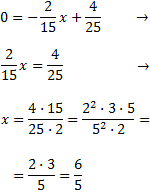
El punto es \((6/5,0)\).
La gráfica de la recta es
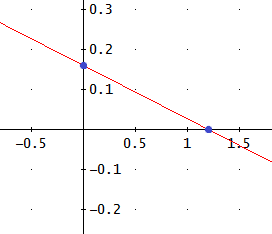
El punto A(1,2) no está en la recta porque no cumple su ecuación:
$$ 5y =\frac{-2x}{3} + \frac{4}{5} $$
$$ 5\cdot 2 \neq \frac{-2\cdot 1}{3} + \frac{4}{5} = \frac{2}{15} $$
Problema 3
Calcular los puntos de corte de los ejes con la recta
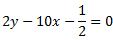
¿Cuál es la pendiente y la ordenada de la recta?
¿El punto A(2, 10.25) es un punto de la recta?
Solución
Escribimos la ecuación en su forma general:
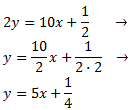
Por tanto, la pendiente es \(a = 5\). Como es positiva, la recta es creciente.
La ordenada de la recta es \( b = 1/4\).
Puntos de corte con el eje OY:
Tiene lugar cuando \(x = 0\). Sustituimos en la ecuación:
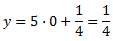
El punto es \((0,1/4)\).
Puntos de corte con el eje OX:
Ocurre cuando \(y=0\). Sustituimos en la ecuación:
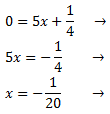
El punto es \((-1/20,0)\).
La gráfica de la recta es
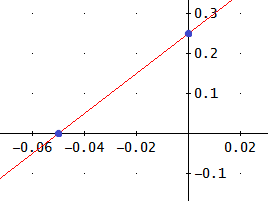
Comprobamos si el punto A(2,10.25) verifica la ecuación:
$$ y = 5x+\frac{1}{4} = 5\cdot 2+\frac{1}{4}=$$
$$ =10 + \frac{1}{4} = \frac{41}{4} = 10.25$$
El punto A sí está en la reca.
Problema 4
Calcular la ecuación de una recta que pase por los puntos A(-3,2) y B(-2,3).
¿Cuántas rectas hay que pasen por los puntos A y B?
Solución
Dados dos puntos A y B distintos, sólo existe una recta que los une.
Tenemos dos formas de resolver el problema:
-
Sustituir las coordenadas de los puntos en la ecuación \(y = ax+b\) para hallar los coeficientes \(a\) y \(b\) resolviendo un sistema de ecuaciones.
-
Deducir la ecuación a partir de alguna ecuación de la recta (como la ecuación continua).
Nosotros seguiremos ambos procedimientos:
Procedimiento 1:
La recta que buscamos debe tener la forma
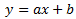
Como los puntos A y B están en la recta que buscamos, deben cumplirla. Sustituimos las coordenadas de los puntos en la ecuación:
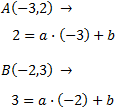
De este modo obtenemos un sistema de ecuaciones:
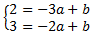
De la primera ecuación obtenemos
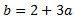
Sustituyendo en la segunda,
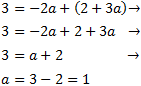
Ya tenemos \( a = 1\). Ahora calculamos \( b\):
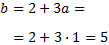
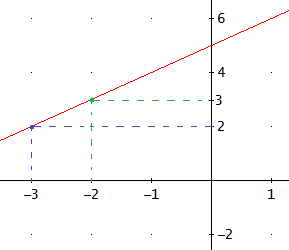
Por tanto, la ecuación de la recta es
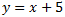
La gráfica de la recta es
Procedimiento 2:
Ahora vamos a calcular la misma recta por otro procedimiento: calculamos la ecuación de la recta a partir de un punto y un vector director de la misma:
La ecuación continua de una recta es de la forma
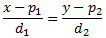
donde \(P = (p_1,p_2)\) es un punto cualquiera de la recta y \(d = (d_1,d_2)\) es un vector director de la recta.
Tomamos como P uno de los puntos dados, por ejemplo, A:
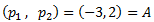
El vector director de la recta es un vector que indica la dirección de la recta. Este vector puede ser el vector que une a ambos puntos de la recta.
Calculamos el vector que une los puntos A y B del enunciado:
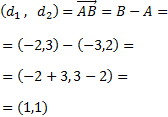
Por tanto, sustituyendo, la ecuación queda como
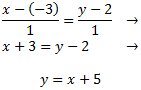
Problema 5
Calcular la recta que pasa por el punto A(7,7) y que tiene pendiente -3. ¿Pasa también por el origen?
Nota: el origen es el punto O(0,0).
Solución
La ecuación de la recta será de la forma
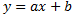
El coeficiente \(a\) debe ser \( a = -3\) puesto que la pendiente de la recta debe ser -3.
Como la recta pasa por el punto A, sus coordenadas verifican la ecuación. Sustituyendo
en la ecuación obtenemos la ordenada \( b\):
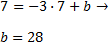
Por tanto, la ecuación de la recta es
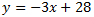
Si la recta pasa por el origen, las coordenadas del orgien deben verificar la ecuación.
Es decir, para \(x = 0\), debemos obtener \(y = 0\), pero obtenemos
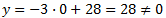
Así que la recta no pasa por el origen.
La gráfica de la recta es
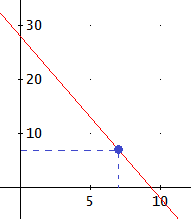
Problema 6
Responder las siguientes cuestiones:
¿Cuántas rectas diferentes hay que pasen por dos puntos distintos A y B?
-
¿Cómo podemos saber si una recta \(y=ax+b\) pasa por un punto P(m, n)?
¿Cuál es la pendiente de una recta horizontal (paralela al eje OX)?
-
Dos rectas (distintas) que no se cortan son rectas paralelas. Las siguientes dos rectas son paralelas:
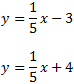
Observando sus ecuaciones, ¿cómo podemos deducir que son paralelas?
Dar ejemplos de otras rectas paralelas a las anteriores.
-
Dada una recta, ¿cuántas rectas (distintas) son paralelas a dicha recta?
Solución
-
Sólo puede haber una recta que pasa por dos puntos (distintos). Notemos
que el segmento que une a ambos puntos forma parte
de dicha recta.
-
Si el punto P de coordenadas \((m,n\)) está en la recta \(y = ax+b\), entonces debe cumplirse que \(n = am + n\). Si la igualdad es falsa, el punto P no está en la recta.
Las rectas horizontales son las que no tienen pendiente, es decir, el coeficiente \(a\) es \(a = 0\). Por tanto, su ecuación es de la forma \(y = b\).
Esto significa que los puntos de la recta son todos los que tienen la segunda coordenada \(y = b\).
-
Las rectas son paralelas porque tienen la mima pendiente (\(a=1/5\)).
Una de ellas pasa por el punto (0,4) y la otra por el punto (0,-3).
Cada una de ellas es la otra desplazada 7 unidades hacia arriba/abajo.
Cualquier recta con pediente \(a = 1/5\) es una recta paralela a las anteriores. Algunos ejemplos son:
$$ y = \frac{1}{5}x $$
$$ y = \frac{1}{5}x +1$$
$$ y = \frac{1}{5}x -1$$
$$ y = \frac{1}{5}x +100$$
-
Existen infinitas rectas paralelas porque \(b\) puede ser cualquier número.
Problema 7
Las siguientes rectas no son paralelas y, por tanto, se cortan en un punto. Calcular dicho punto:
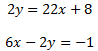
El punto donde dos rectas se cortan se denomina punto de intersección.
Solución
Primero escribimos las ecuaciones en su forma general:
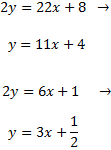
En efecto, como las pendientes son distintas (11 y 3), las rectas no son paralelas y,
por tanto, se cortan en algún punto. Es decir, existe un valor de \(x\) para
el que ambas funciones valen lo mismo.
Para calcular el punto de intersección (punto común de las rectas), igualamos ambas ecuaciones
y obtenemos una ecuación de primer grado:
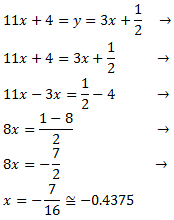
Ahora calculamos la segunda coordenada:
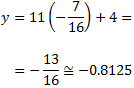
Por tanto, el punto intersección (donde se cortan) es
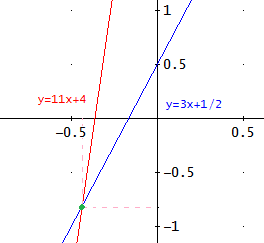
Las gráficas de las ecuaciones son
Problema 8
Las gráficas de las siguientes rectas se cortan en los vértices de un triángulo. Escribir los puntos de los vértices y calcular la longitud de la base del triángulo:
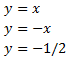
Solución
Tenemos que calcular los puntos de intersección de las tres rectas dos a dos.
Intersección de la primera recta con la segunda:
Igualamos las \(y\):
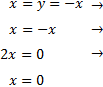
El primer vértice es \((0,0)\).
Intersección de la primera recta con la tercera:
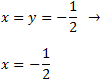
El segundo vértice es \((-1/2, -1/2)\).
Intersección de la segunda recta con la tercera:
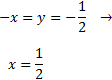
El tercer vértice es \((1/2, -1/2)\).
Representamos las rectas para visualizar el triángulo:
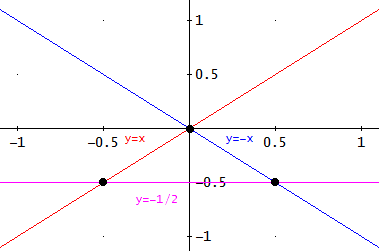
La base es el segmento que une los dos últimos puntos, es decir, su longitud es
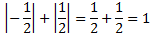
Hemos usado valores absolutos ya que las longitudes han de ser positivas.
Problema 9
Encontrar, si existen:
-
la recta que une los tres puntos A(-1, -15), B(3, 9) y C(2, 3);
-
la recta que une los tres puntos D(0,9), E(-2, 21) y F(8, 0).
Dados 3 puntos distintos, ¿siempre existe una recta que los une?
Solución
No siempre existe una recta que une a tres puntos distintos. Para que exista, los tres puntos tienen que
estar alineados.
Como no sabemos si los tres puntos están alineados, calculamos la recta que une a dos de ellos y luego comprobamos
si el tercero está en dicha recta.
Para calcular la recta que une A y B, podemos resolver el sistema de ecuaciones que se obtiene al sustituir las coordenadas de los puntos en la ecuación general (este procedimiento lo seguiremos en el segundo apartado del problema).
Por variar, en este apartado usaremos la ecuación continua de una recta, indicada en el Procedimiento 2 del Problema 4:
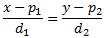
donde \(P = (p_1,p_2)\) es un punto cualquiera de la recta
y \(d = (d_1,d_2)\) es un vector director de la recta.
El vector director de la recta lo podemos obtener a partir de dos puntos (el vector que los une).
Tomamos como P uno de los puntos dados, por ejemplo, A:
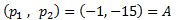
Calculamos el vector que une los puntos A y B del enunciado:
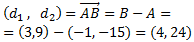
Sustituimos en la ecuación:
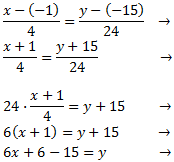
La ecuación es
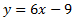
Comprobamos si el punto C(2,3) está en la recta. Al sustituir \(x = 2\) en la
ecuación tenemos que obtener \(y = 3\).
En efecto,
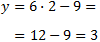
Por tanto, los puntos están alineados y la recta los une a los tres.
Apartado 2: recta que une los puntos D(0,9), E(-2,21) y F(8,0).
Puesto que en los puntos D y F tenemos ceros, podemos calcular fácilmente
la recta que los une sustituyendo en la ecuacón general \( y = ax+b\):
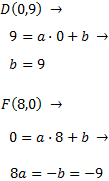
Por tanto, la recta que une los puntos D y F es
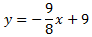
Comprobamos si el punto E(-2,21) está en dicha recta. Para \(x = -2\) tenemos que obtener \(y = 21\),
pero obtenemos 45/4:
$$ y = -\frac{9}{8}x + 9 = $$
$$ = -\frac{9}{8}\cdot(-2) + 9 = $$
$$ = \frac{18}{8} + 9 = \frac{45}{4}$$
Es decir, lo puntos no están alineados y por tanto, no existe una recta que los
una a los tres.
Problema 10 (dificultad alta)
Dos rectas que se cortan formándo un ángulo de 90 grados se dice que son rectas perpendiculares.
Por ejemplo, los ejes del plano son rectas perpendiculares.
Encontrar una recta perpendicular a la recta \( y = ax +b\) siendo \(a\neq 0\).
Ayuda:
-
\(v = B - A\) es un vector director de la recta que une a los puntos A y B.
-
Si los vectores directores de dos rectas son perpendiculares, las rectas también lo son.
-
Los vectores \((a_1, a_2)\) y \((b_1, b_2)\) son perpendiculares si
$$ a_1 \cdot b_1 + a_2 \cdot b_2 = 0 $$
El producto anterior se denomina producto escalar de vectores.
Solución
Buscamos dos puntos de la recta para obtener un vector director de ésta.
Sustituimos \(x = 0\) y \(x = 1\) en la ecuación \(y = ax+b\) para obtener dos puntos de la recta \( y = ax+b\):
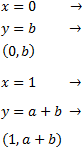
Por tanto, los puntos \((0,b)\) y \((1,a+b)\) son dos puntos de la recta \(y = ax+b\).
Un vector director de la recta es el vector que une a los puntos anteriores:
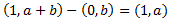
Consideremos la ecuación de la recta perpendicular. Su ecuación general será de la forma
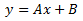
Razonando del mismo modo que en la recta \(y = ax+b\), un vector de la recta perpendicular es
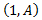
Como las rectas son perpendiculares, los vectores directores forman un ángulo de 90 grados, es decir,
son perpendiculares. Por tanto, su producto escalar de vectores es 0, es decir,
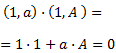
Por tanto,
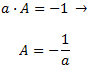
Por tanto, las rectas perpendiculares a la recta \(y=ax+b\) son de la forma
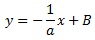
Es decir, son las rectas con pendiente inversa y de signo opuesto (siempre que la pendiente no sea 0).
Según el valor de la ordenada \(B\) de la recta, tendremos una u otra recta, pero todas son perpendiculares a la recta \( y = ax+b\). Lo mismo ocurre con \(b\).
Es decir, aunque cambiemos los valores de \(b\) y de \(B\), las rectas \(y = ax+b\) e \(y = -\frac{1}{a}x +B\) son perpendiculares.
4. Problemas sobre parábolas
Problema 1
Calcular los puntos de corte de la siguiente parábola con los ejes de coordenadas:
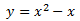
Solución
Podemos escribir la ecuación en forma factorizada como
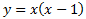
Puntos de corte con el eje de abscisas (eje OX):
Oocurre cuando \(y = 0\). Sustituimos en la ecuación y obtenemos
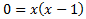
Como la ecuación de segundo grado está factorizada no es necesario aplicar la fórmula cuadrática. Las soluciones son \(x=0\) y \(x =1\).
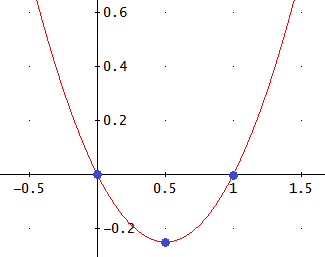
Luego tenemos dos puntos de corte:
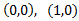
Puntos de corte con el eje de ordenadas (eje OY):
Ocurre cuando \(x=0\). Sustituimos en la ecuación y obtenemos
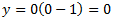
El punto es (0,0).
Notemos que hemos obtenido el punto (0,0) (el origen) como punto de corte con el
eje de abscisas y el de ordenadas. Y es que, en efecto, en el origen,
la parábola corta a los dos ejes.
Calculamos ahora el vértice y con los puntos de corte y el vértice podemos representar fácilmente la parábola.
Para calcular el vértice, identificamos los coeficientes \(a\), \(b\) y \(c\) y aplicamos la fórmula:
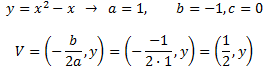
El valor de \(y\) lo obtenemos sustituyendo el valor de \(x\) en la ecuación:
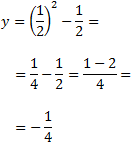
El vértice es
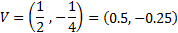
La gráfica es
Problema 2
Encontrar las dos parábolas que cortan al eje de abscisas (eje OX) en los puntos A(0,0) y B(2,0), pero con vértices distintos: (1,-5) y (1,-2).
Solución
La ecuación general de una parábola es
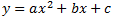
Sabemos que las dos parábolas pasan por los puntos
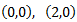
Luego dichos punto verifican la ecuación. Los sustituimos en la ecuación general para calcular los coeficientes de las parábolas:
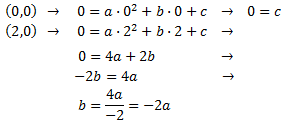
Por tanto, las ecuaciones de ambas parábolas son de la forma
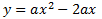
El valor de \(a\) lo obtendremos a partir de los vértices, que son

Sustituimos el primer vértice en la ecuación:
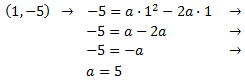
Por tanto, una de las parábolas es
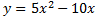
Sustituimos el segundo vértice en la ecuación:
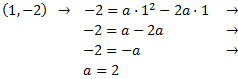
Luego la otra parábola es
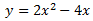
Con los 3 puntos de cada parábola podemos representarlas rápidamente:
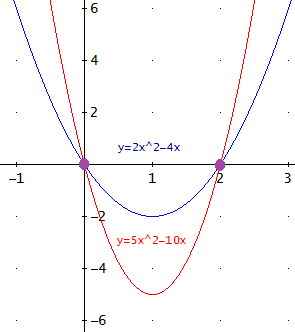
Problema 3
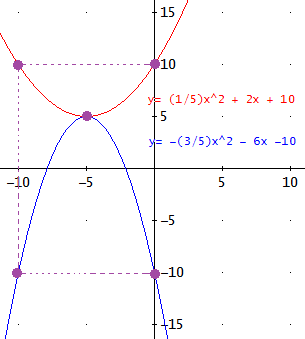
Calcular las dos parábolas que tienen el vértice en el mismo punto V(-5,5), sabiendo que una corta al eje de ordenadas (eje OY) en el punto (0,10) y pasa por (-10,10) y la otra corta al eje de ordenadas en el punto (0,-10) y pasa por (-10,-10).
Solución
La ecuación general de las parábolas es
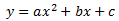
Usaremos primero el vértice, que es común en ambas parábolas.
Como las parábolas pasan por (-5,5), dicho punto verifica
ambas ecuaciones. Sustituimos:
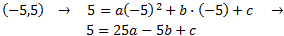
Sabemos que una de ellas pasa por (0,10) y por (-10,10) . Sustituimos en la ecuación:
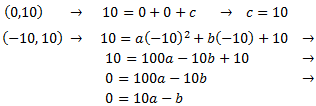
Al sustituir la \( c\), la ecuación que teníamos al principio queda como
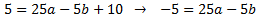
Ahora tenemos un sistema de dos ecuaciones y dos incógnitas (a y b) para la primera parábola
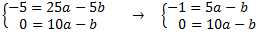
De la segunda ecuación obtenemos que
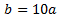
Sustituyendo en la primera
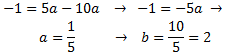
Por tanto, tenemos la parábola
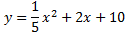
Para calcular la otra parábola procedemos de igual modo:
Sabemos que pasa por (0,-10) y por (-10,-10) . Sustituimos en la ecuación:
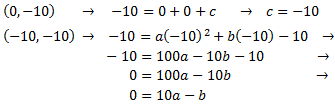
Al sustituir la \(c\), la ecuación que teníamos al principio queda como
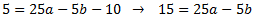
Ahora tenemos un sistema de dos ecuaciones y dos incógnitas (a y b)

De la segunda ecuación obtenemos que
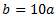
Sustituyendo en la primera
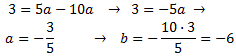
Por tanto, tenemos la parábola
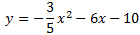
Las gráficas son
Problema 4
Dar un ejemplo de una parábola que no corta al eje de abscisas (eje OX), de otra que lo corta en un solo punto y de otra que lo corta en dos puntos.
Solución
La ecuación general de una parábola es
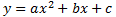
La parábola corta al eje de abscisas (eje OX) cuando \(y=0\). Es decir, para los valores de \(x\) que cumplen
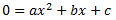
Tenemos una ecuación de segundo grado. Esta es la razón de que las parábolas cortan al eje OX en un punto, en dos puntos o en ninguno, depende del número de soluciones que tiene
la ecuación.
Sabemos el número de soluciones calculando su discriminante:
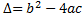
-
Si Δ > 0, tiene dos soluciones distintas (dos puntos de corte).
Si Δ = 0, tiene una única solución (un punto de corte).
Si Δ < 0, no tiene soluciones (no hay punto de corte).
Podemos tomar, por ejemplo, los valores \(a=c=1\). Así, el discriminante es
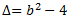
Ahora, damos algunos valores a \(b\) para tener discriminantes distintos:
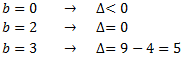
Así, tenemos
Parábola que no corta al eje:
$$y=x^2+1$$
-
Parábola que corta al eje en un punto:
$$y=x^2+2x+1$$
-
Parábola que corta al eje en dos puntos:
$$y=x^2+3x+1$$
La gráficas son
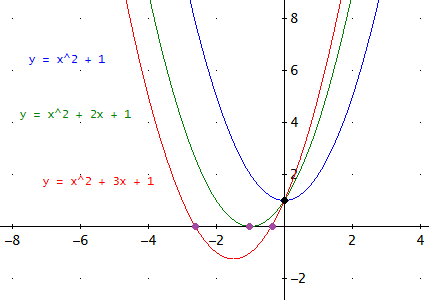
Como comentario, podemos decir que las tres parábolas pasan por un mismo punto (0,1). Esto se debe a que tienen el mismo término independiente \(c=1\).
Problema 5
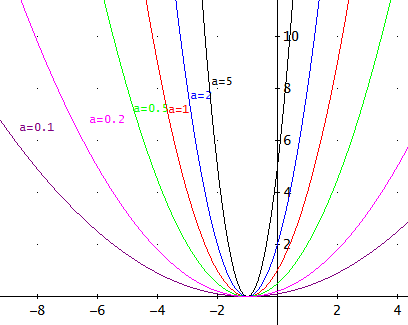
Para cada valor del parámetro \(a\), consideramos la parábola de ecuación
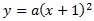
Calcular los puntos de corte con los ejes de ordenadas y de abscisas.
-
¿Qué diferencia hay entre las parábolas que tienen \(a > 0\) y las que tienen \(a < 0\) ?
Si \(a\) es positivo, ¿cómo cambia la parábola cuando \(a\) es un número más grande?
Solución
Puntos de corte con el eje de abscisas (eje OX): ocurre cuando
\( y = 0\).
Tenemos que resolver la ecuación
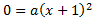
Al estar en forma factorizada, sabemos que la única solución es \(x = -1\).
Por tanto, el punto es (0,-1).
Puntos de corte con el eje de ordenadas (eje OY): ocurre cuando \( x = 0\).
Por tanto,
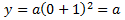
El punto es (0,a).
-
Las parábolas con \(a >0\) tienen forma de U; las parábolas con \(a < 0\)
tienen forma de U invertida. Esto se debe a que \(a\) el es coeficiente del
monomio de mayor grado (\(x^2\)), por lo que su signo tiene
más peso al calcular \( y\).
En nuestro caso,
$$y=a(x+1)^2$$
el signo de \( y\) es el mismo que el de \( a\). Luego si \(a > 0\), a medida
que crece \( x\), crece \( y\) (forma de U); y si \(a < 0\), a medida que
crece \( x\), decrece \( y\) (forma de U invertida).
Las parábolas con un valor de \( a\) mayor crecen más rápido, lo que significa
que la parábola será más cerrada.
Veamos ejemplos para algunos valores de \( a\):
Problema 6
Dada la parábola
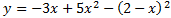
calcular la parábola que se obtiene al aplicarle una simetría respecto
del eje de las abscisas.
Hay algunos puntos que coinciden en ambas
parábolas. ¿Cuáles y por qué?
Solución
Antes de todo vamos a escribir la parábola en la forma general.
Para ello tenemos que desarrollar el cuadrado de la suma:
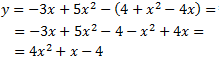
Una simetría respecto del eje OX es como darle la vuelta al plano (girando por dicho eje).
Para ello, cambiamos el signo a la segunda coordenada \( y\) de todos los puntos.
Por tanto, la nueva parábola es
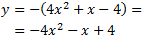
Las gráficas son
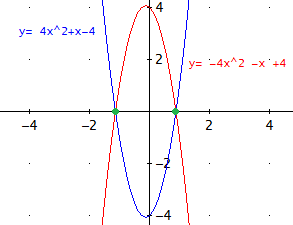
Los puntos en las que las parábolas coinciden son la intersección
y los podemos calcular igualando las parábolas.
Pero no es necesario, ya que estos puntos son los que
tienen 0 en la segunda coordenada y, por tanto, no cambia al cuando aplicamos la simetría (porque 0 no tiene signo).
Calculamos los puntos:
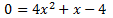
Resolvemos la ecuación de segundo grado:
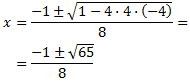
Por tanto, son los puntos
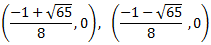
Problema 7
Calcular la parábola que resulta al desplazar 3 unidades hacia arriba la parábola
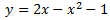
Y la parábola que resulta si, en vez de hacia arriba, la desplazamos hacia la derecha 3 unidades.
Solución
Desplazar la parábola hacia arriba 3 unidades significa sumar 3 a la
segunda coordenada, es decir, a \( y\). Por tanto, la parábola es
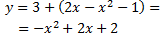
Las gráficas son
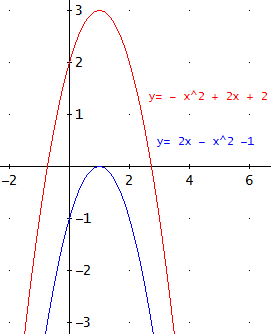
Desplazar la parábola 3 unidades hacia la derecha significa que para cada x, la \( y\) tiene que valer lo que valía para \( x -3\).
Por tanto, lo que hay que hacer es cambiar \( x\) por \(x-3\). La ecuación queda como
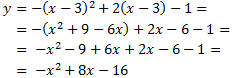
Las gráficas son
Problema 8
Foco y directriz de una parábola.
Consideremos las parábolas que pueden escribirse como
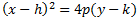
siendo \(h,\ p,\ k\) parámetros (números fijos). Entonces, el foco de la parábola es el punto \(( h , k + p )\), el vértice es \(( h , k )\) y la directriz es la recta \(y = k - p\).
Se cumple que la distancia de un punto de la parábola al foco es la misma que la distancia de dicho punto a la directriz.
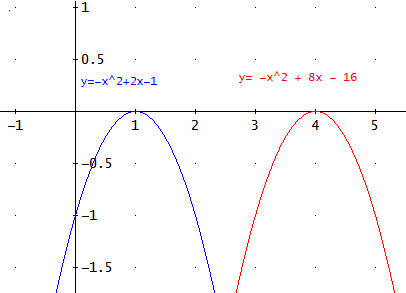
Calcular el foco y la directriz de las siguientes parábolas:
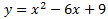
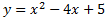
Solución
1. Tenemos que operar en la ecuación para conseguir la forma del enunciado:
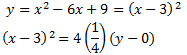
Así, podemos identificar los parámetros:
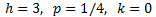
El foco es (3,1/4), el vértice es (3,0) y la directriz es \(y = -1/4\).
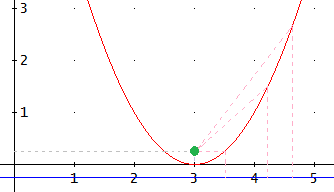
2. Operamos en la ecuación
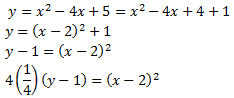
Luego los coeficientes son
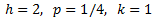
El foco es (2, 5/4), el vértice es (2,1) y la directriz es y=3/4.
Problema 9
El eje de simetría de todas las parábolas vistas anteriormente es vertical (paralelo al eje OY).
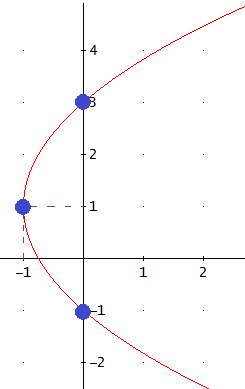
La ecuación
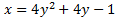
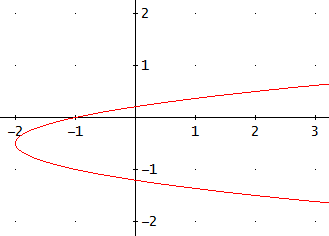
es una parábola con eje de simetría horizontal (paralelo al eje OX) y, a diferencia de las anteriores, corta al eje OY en dos puntos.
Calcular los puntos de corte y el vértice de la parábola anterior.
Solución
La única diferencia con las otras parábolas es que hemos
cambiado la \( x\) por la \( y\) y, por ello, la
parábola está rotada (hemos girado el plano).
Los puntos de corte con el eje OX tienen lugar cuando \( y = 0\).
Sustituyendo en la ecuación, tenemos que \(x = -1\). Por tanto,
el único punto de corte es (-1,0)
Los puntos de corte con el eje OY tienen lugar
cuando \( x = 0\). Resolvemos la ecuación de segundo grado
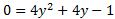
cuyas soluciones son
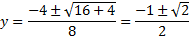
Por tanto, los puntos de corte son
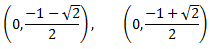
La gráfica es
Problema 10
Calcular la parábola con eje de simetría horizontal que tiene el vértice en el punto (-1,1) y corta al eje OY en los puntos (0,3) y (0,-1).
Solución
La ecuación general de una parábola (con eje de sietía horizontal) es
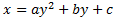
Sabemos que para una parábola de eje de simetría vertical el vértice
es el punto
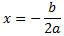
Al cambiar el eje, cambiamos la \( x\) por la \( y\). Como el
vértice está en (-1,1),
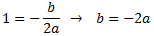
La equación queda
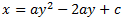
Por otro lado, sabemos que la parábola pasa por los
puntos (0,3) y (0,-1) Sustituyendo en la ecuación obtenemos:
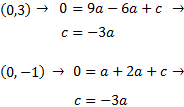
Por tanto,
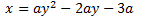
Usamos de nuevo el vértice (-1,1) para calcular el término \(a\) de la ecuación:
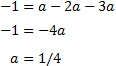
Luego la ecuación de la parábola que buscamos es
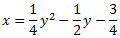
Y su gráfica es