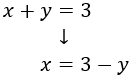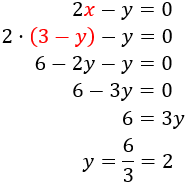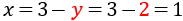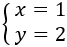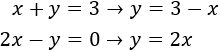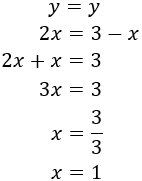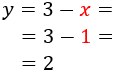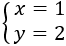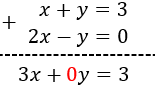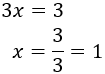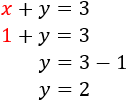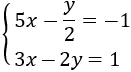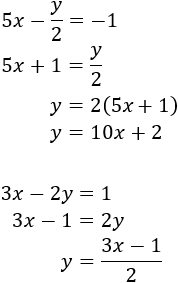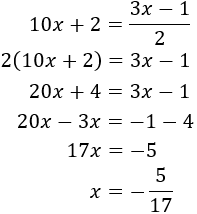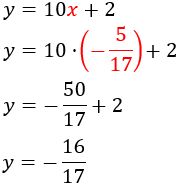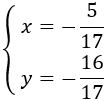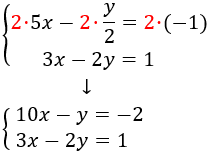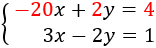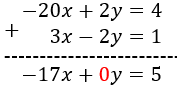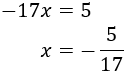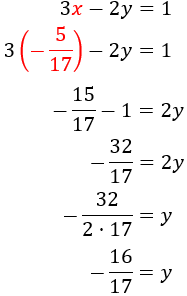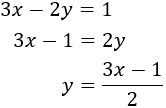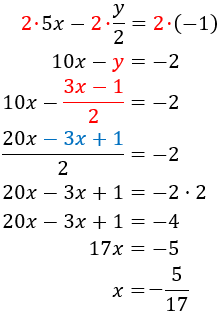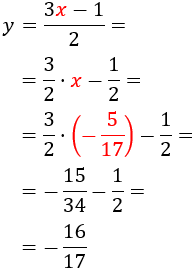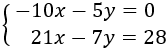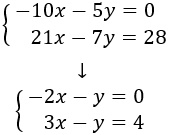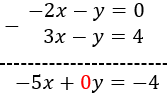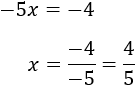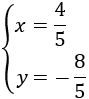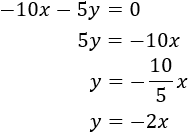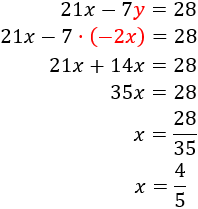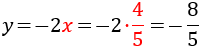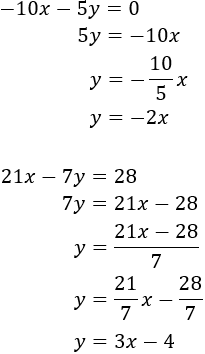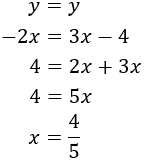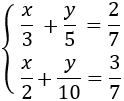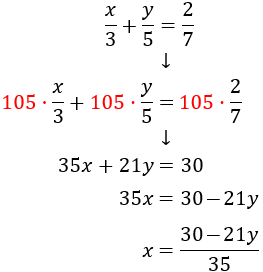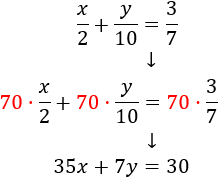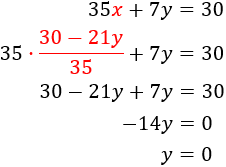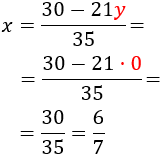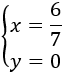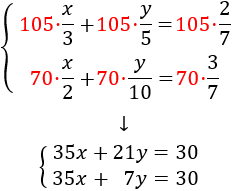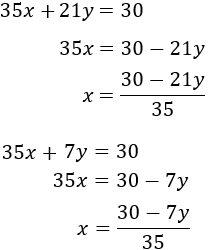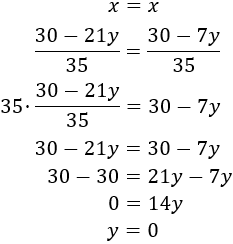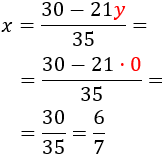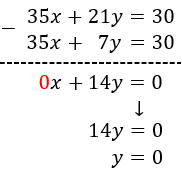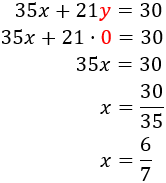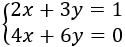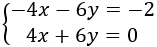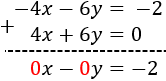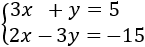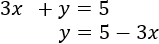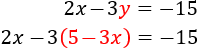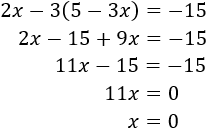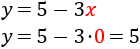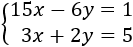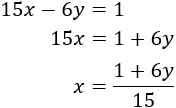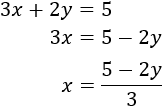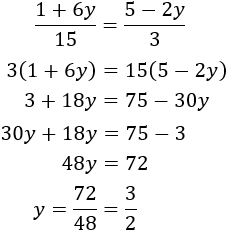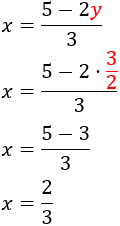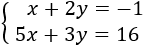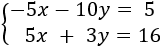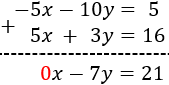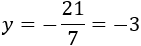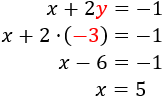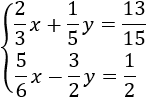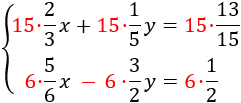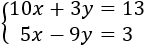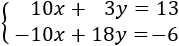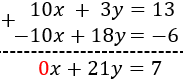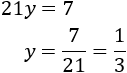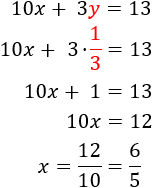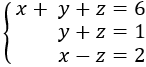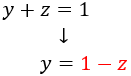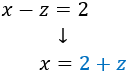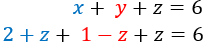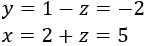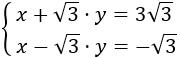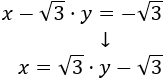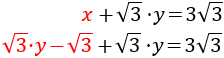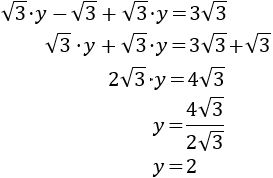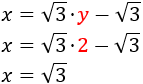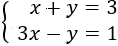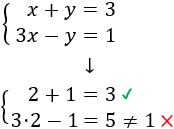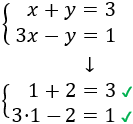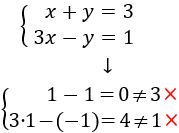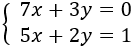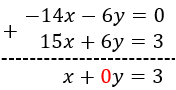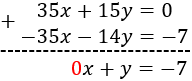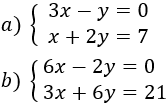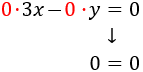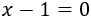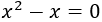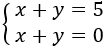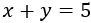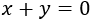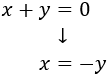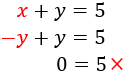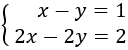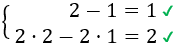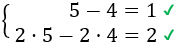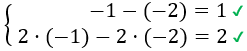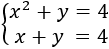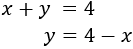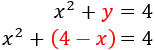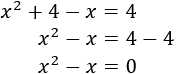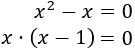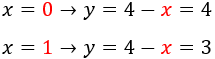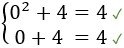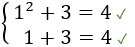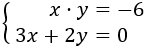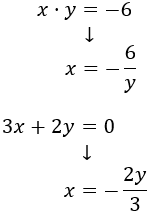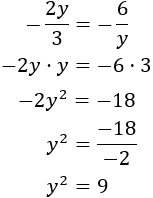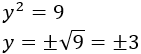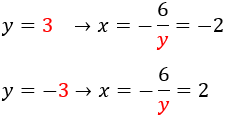Resolveremos:
-
4 sistemas de ecuaciones lineales por los 3 métodos básicos (sustitución, igualación y reducción)
-
7 sistemas de ecuaciones lineales por uno de los 3 métodos básicos
-
5 problemas sobre sistemas para pensar
-
2 sistemas de ecuaciones no lineales (uno por sustitución y otro por igualación)
Sistema 1 

Resolvemos por SUSTITUCIÓN:
Como la primera ecuación es más simple, despejamos una incógnita en dicha ecuación, por ejemplo, la \(x\):
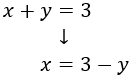
Ahora, sustituimos la \(x\) en la otra ecuación, es decir, donde aparece \(x\), escribimos \(3-y\). De este modo, obtenemos una ecuación con una única incógnita (\(y\)) y podemos resolverla fácilmente:
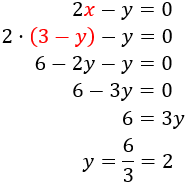
Como ya tenemos el valor de la incógnita \(y\), sólo falta calcular la otra incógnita. Para ello, podemos usar la expresión (la fórmula) que obtuvimos en el primer paso (escribimos \(2\) en lugar de \(y\)):
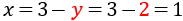
Por tanto, la solución del sistema es \(x=1\) e \(y = 2\):
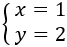
Ver Igualación

Despejamos en ambas ecuaciones la \(y\):
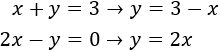
Como \(y = y\), igualamos las expresiones y resolvemos la ecuación:
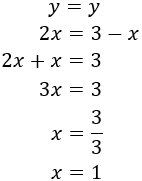
Ahora, sustituimos el valor de la incógnita \(x = 1\) en la primera de las
ecuaciones anteriores para calcular \(y\):
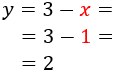
Por tanto, la solución del sistema es \(x = 1\) e \(y = 2\):
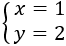
Ver Reducción

Para sumar las ecuaciones y que desaparezca una
de las dos incógnitas, los coeficientes de dicha incógnita deben ser iguales, pero de signo distinto.
Observad que la incógnita \(y\) tiene coeficiente 1 en la primera ecuación y -1 en la segunda, así que esta incógnita desaparece al sumar las ecuaciones sin necesidad de más operaciones:
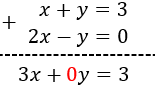
Calculamos \(x\) resolviendo la ecuación de primer grado obtenida:
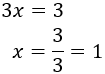
Finalmente, sustituimos \(x = 1\) en una de las dos ecuaciones para obtener \(y\):
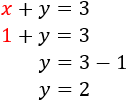
Por tanto, la solución del sistema de ecuaciones es \(x = 1\) e \(y = 2\).
Sistema 2 
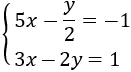
Resolvemos por IGUALACIÓN:
Tenemos que despejar la misma incógnita en las dos ecuaciones para, posteriormente, igualar ambas expresiones obtenidas.
Elegimos despejar la incógnita \(y\) porque así desaparecerá el denominador y será más fácil trabajar.
Despejamos en ambas ecuaciones la \(y\):
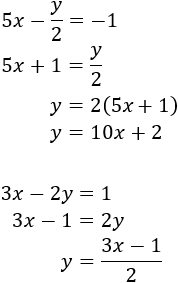
Igualamos ambas expresiones para obtener una ecuación con una sola incógnita (\(x\)) y la resolvemos:
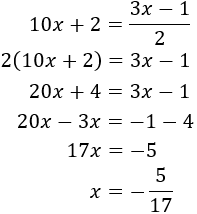
Como ya tenemos el valor de \(x\), sustituimos en cualquiera de las expresiones obtenidas para calcular el valor de la incógnita \(y\). Escogemos la primera expresión que obtuvimos:
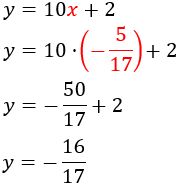
Por tanto, la solución del sistema es \(x=-5/17\) e \(y = -16/17\):
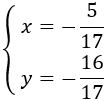
Ver Reducción
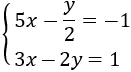
Lo primero que haremos es eliminar el denominador. Para ello, multiplicamos la primera ecuación por 2:
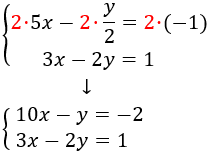
Observad que si multiplicamos la primera ecuación por -2, entonces la incógnita \(y\) desaparece al sumar las ecuaciones. Multiplicamos la primera ecuación por -2:
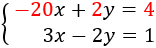
Sumamos las ecuaciones:
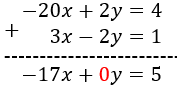
Por tanto, ya podemos calcular la \(x\):
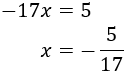
Sustituimos el valor de \(x\) en cualquiera de las ecuaciones del sistema, por ejemplo, la segunda:
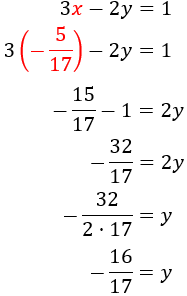
Por tanto, la solución del sistema es \(x = -5/17\) e \(y = -16/17\):
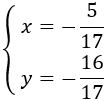
Ver Sustitución
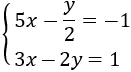
Despejamos en la segunda ecuación la \(y\):
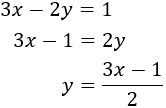
Ahora tenemos que sustituir la expresión obtenida para \(y\) en la primera ecuación y resolverla. No obstante, antes de eso vamos a multiplicar la primera ecuación por 2 para eliminar el denominador:
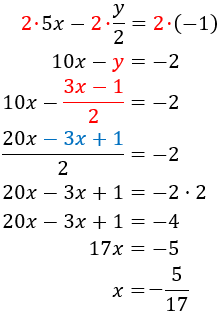
Nota: observad que hemos señalado en azul que hemos cambiado el signo de los sumandos del numerador porque la fracción tiene un signo negativo delante.
Como ya conocemos \(x\), calculamos \(y\) sustituyendo en alguna de las ecuaciones anteriores (o la propia expresión de \(y\) calculada inicialmente):
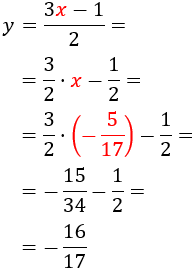
Por tanto, la solución del sistema es \(x = -5/17\) e \(y = -16/17\):
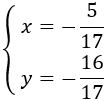
Sistema 3 
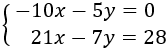
Resolvemos por REDUCCIÓN:
Antes que nada, podemos multiplicar la primera ecuación por la fracción 1/5 y la segunda por la fracción 1/7. De este modo, vamos a transformar el coeficiente de la incógnita \(y\) en -1:
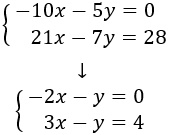
Si RESTAMOS las dos ecuaciones, ya desaparece la incógnita \(y\):
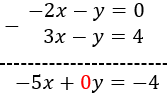
Con lo que ya podemos calcular \(x\):
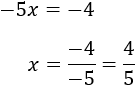
Calculamos la otra incógnita a partir de cualquiera de las ecuaciones del sistema:

Por tanto, la solución del sistema es \(x = 4/5\) e \(y = -8/5\):
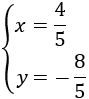
Ver Sustitución
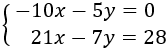
Despejamos en la primera ecuación la \(y\):
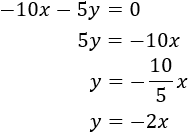
Sustituimos su expresión en la segunda ecuación y la resolvemos:
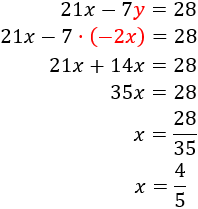
Calculamos \(y\) sabiendo \(x=4/5\):
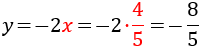
Por tanto, la solución del sistema es
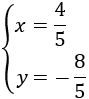
Ver Igualación
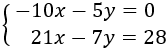
Despejamos en ambas ecuaciones la incógnita \(y\):
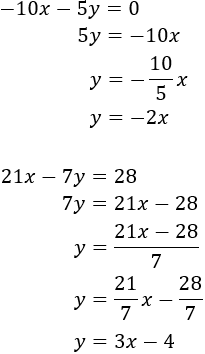
Igualamos las expresiones obtenidas y resolvemos la ecuación:
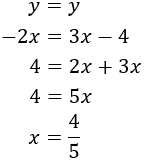
Sustituyendo \(x = 4/5\) en la primera de las ecuaciones anteriores obtenemos:
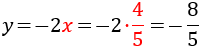
Por tanto, la solución del sistema es
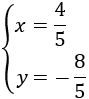
Sistema 4 
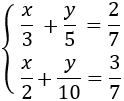
Resolvemos por SUSTITUCIÓN:
Antes que nada, será mejor multiplicar cada ecuación por el mínimo común múltiplo (mcm) de sus denominadores para evitar trabajar con fracciones.
El mínimo común múltiplo de 3, 5 y 7 es su producto, porque son números primos: es 105.
Multiplicamos la primera ecuación por 105 y aislamos las \(x\):
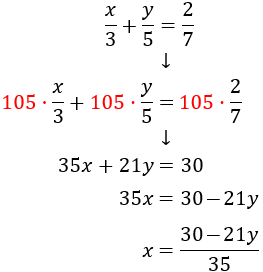
El mcm de 2, 10 y 7 es 70. Multiplicamos la segunda ecuación por 70:
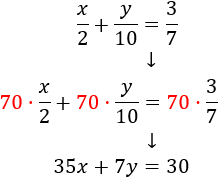
Sustituimos en esta ecuación la \(x\) que acabamos de calcular:
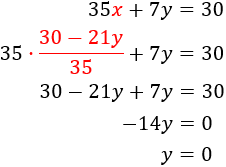
Calculamos \(x\) sabiendo \(y=0\):
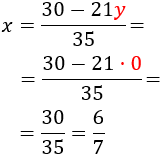
Por tanto, la solución del sistema es \(x = 6/7\) e \(y = 0\):
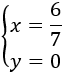
Ver Igualación
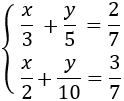
Podemos multiplicar las ecuaciones por el mínimo común múltiplo (mcm) de sus denominadores para evitar las fracciones. El mcm de 3, 5 y 7 es 105 y el de 2, 7 y 10 es 70.
Multiplicamos la primera ecuación por 105 y la segunda por 70:
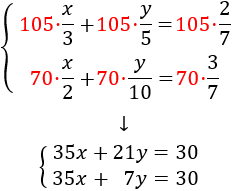
Despejamos en las dos ecuaciones la \(x\):
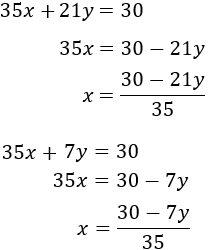
Igualamos ambas expresiones y resolvemos la ecuación:
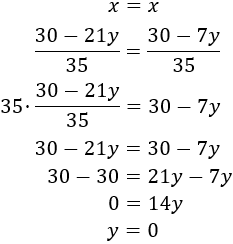
Sustituyendo \( y = 0\) en la primera de las expresiones anteriores,
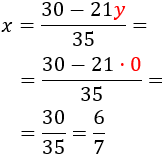
Por tanto, la solución del sistema es
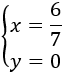
Ver Reducción
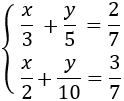
Para evitar las fracciones, multiplicamos la primera ecuación por 105 y la segunda por 70 (son el mínimo común múltiplo de los denominadores de la primera y la segunda ecuación, respectivamente):
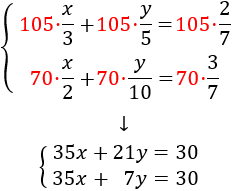
Restamos las ecuaciones y desaparece la incógnita \(x\):
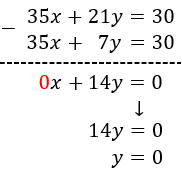
Sustituimos el valor \(y=0\) en la primera ecuación y la resolvemos:
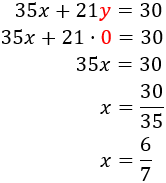
Por tanto, la solución del sistema es
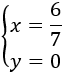
Sistema 5 
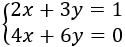
Resuelve por reducción.
Resolvemos por REDUCCIÓN:
Si multiplicamos la primera ecuación por -2 y sumamos las dos ecuaciones, desaparece la incógnita \(x\) (en realidad, la \(y\) también).
Multiplicamos la primera ecuación por -2:
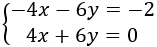
Sumamos las ecuaciones:
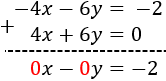
Por tanto, tenemos
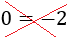
Esta igualdad es obviamente falsa (0 no es igual a -2), lo que significa que el sistema no tiene solución. No hay ningún par de valores para \(x\) e \(y\) que hagan que se cumplan ambas ecuaciones simultáneamente.
Este sistema no tiene solución: se dice que es un sistema INCOMPATIBLE.
Sistema 6 
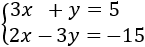
Resuelve por sustitución.
Resolvemos por SUSTITUCIÓN:
Tenemos que aislar una de las incógnitas en una de las ecuaciones y sustituir en la otra. Lo más rápido es aislar la \(y\) en la primera ecuación (porque no tiene coeficiente):
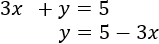
Sustituimos en la segunda ecuación:
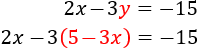
Resolvemos la ecuación:
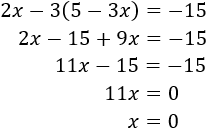
Ahora ya podemos calcular la otra incógnita:
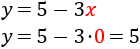
Por tanto, la solución del sistema es \(x = 0\) e \(y = 5\).
Sistema 7 
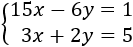
Resuelve por igualación.
Resolvemos por IGUALACIÓN:
Vamos a aislar, por ejemplo, la \(x\), en ambas ecuaciones. Después, igualamos y resolvemos la ecuación.
Primera ecuación:
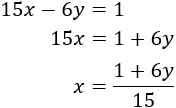
Segunda ecuación:
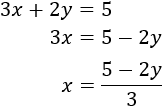
Igualamos ambas expresiones y resolvemos la ecuación:
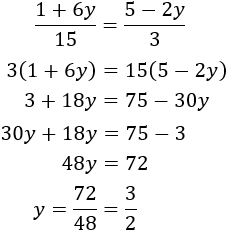
Ahora ya podemos calcular la otra incógnita:
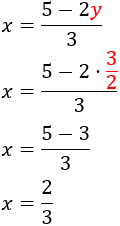
Por tanto, la solución del sistema es \(x = 2/3\) e \(y = 3/2\).
Sistema 8 
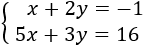
Resuelve por reducción.
Resolvemos por REDUCCIÓN:
Si multiplicamos la primera ecuación por -5, al sumar las ecuaciones obtendremos una ecuación con una sola incógnita.
Multiplicamos la primera ecuación por -5:
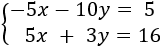
Sumamos las ecuaciones:
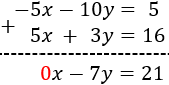
Por tanto, tenemos
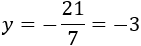
Calculamos la otra incógnita sustituyendo \(y = -3\) en una de las ecuaciones (por ejemplo, la primera):
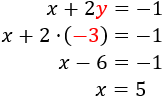
Por tanto, la solución del sistema es \(x = 5\) e \(y = -3\).
Sistema 9 
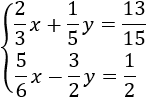
Resuelve por reducción.
Resolvemos por REDUCCIÓN:
El mínimo común múltiplo (mcm) de los denominadores de las fracciones de la primera ecuación es 15; el de la segunda es 6. Multiplicamos cada ecuación por su mcm y así nos deshacemos de las fracciones:
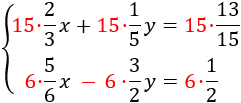
Operamos un poco para simplificar:
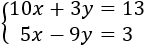
Ahora, si multiplicamos la segunda ecuación por -2, cuando sumemos las ecuaciones desaparece la incógnita \(x\).
Multiplicamos por -2 la segunda ecuación:
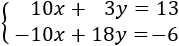
Sumamos las ecuaciones:
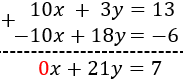
Por tanto, tenemos
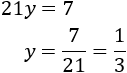
Calculamos \(x\) a partir de la primera ecuación:
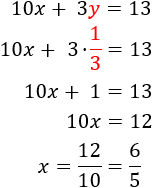
Luego la solución del sistema es \(x = 6/5\) e \(y = 1/3\).
Sistema 10 
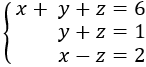
Resuelve por sustitución.
Resolvemos por SUSTITUCIÓN:
En este sistema tenemos 3 ecuaciones con 3 incógnitas, pero podemos resolverlo fácilmente por el método de sustitución: podemos aislar la \(y\) en la segunda ecuación y la \(x\) en la tercera para sustituirlas en la primera.
Aislamos \(y\) en la segunda ecuación:
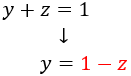
Aislamos \(x\) en la tercera ecuación:
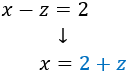
Sustituimos \(x\) e \(y\) en la primera ecuación:
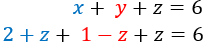
Resolvemos la ecuación:

Calculamos las otras incógnitas:
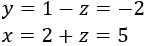
Por tanto, la solución del sistema es \(x = 5\), \(y = -2\) y \(x = 3\).
Sistema 11 
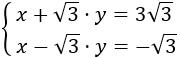
Resuelve por sustitución.
Resolvemos por SUSTITUCIÓN:
Las raíces asustan un poco, pero las tratamos como si fuesen números enteros o fracciones.
Aislamos la \(x\) en la segunda ecuación:
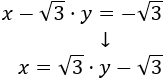
Sustituimos en la primera ecuación:
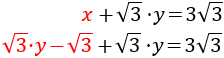
Resolvemos la ecuación:
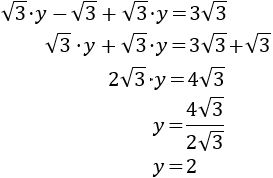
Finalmente, calculamos \(x\):
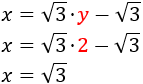
Luego la solución del sistema es \(x = \sqrt{3}\) e \(y = 2\).
Problema 1 
Consideremos el siguiente sistema:
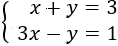
Determinar si alguna de las siguientes opciones es solución del sistema y explicar por qué:
-
\(x = 2\) e \(y =1\)
-
\(x = 1\) e \(y =2\)
-
\(x = 1\) e \(y =-1\)
SOLUCIÓN:
La solución ha de verificar AMBAS ecuaciones. Comprobamos si es así:
Si \(x = 2\) e \(y =1\), entonces
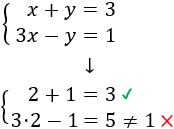
Verifica la primera ecuación, pero no la segunda. NO es solución del sistema.
Si \(x = 1\) e \(y =2\), entonces
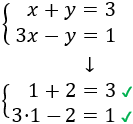
Verifica ambas ecuaciones: ES solución del sistema.
Si \(x = 1\) e \(y =-1\), entonces
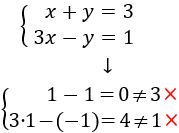
No verifica ninguna de las ecuaciones: NO es solución.
Problema 2 
Se quiere resolver el siguiente sistema por el método de reducción:
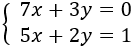
-
¿Por qué números deberíamos multiplicar cada una de las ecuaciones para eliminar la incógnita \(y\) al sumar ambas ecuaciones?
-
¿Y si quisiéramos eliminar la \(x\)?
-
¿Cuál es la solución del sistema?
SOLUCIÓN:
Para eliminar la incógnita \(y\) al sumar ambas ecuaciones, sus coeficientes deben ser el mismo, pero de signo contrario.
Podemos, por ejemplo, multiplicar la primera ecuación por -2 y la segunda por 3:
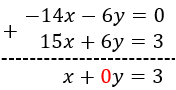
Para eliminar la \(x\), podemos multiplicar la primera ecuación por 5 y la segunda por -7:
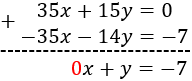
Observad que la solución del sistema es \(x =3\) e \(y = -7\).
Problema 3 
-
Sin necesidad de resolver los siguientes sistemas podemos afirmar que tienen la misma solución. ¿Sabrías decir por qué?
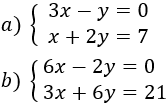
-
¿Qué pasaría si multiplicamos una ecuación del sistema por 0? ¿Y si multiplicamos por una de las incógnitas?
SOLUCIÓN:
Apartado 1.
Multiplicar una ecuación por un número distinto de 0 no cambia su solución: son ecuaciones EQUIVALENTES.
Los dos sistemas del problema son EQUIVALENTES (tienen la misma solución) porque sus ecuaciones son equivalentes entre sí:
-
La primera ecuación del sistema b es la primera ecuación del sistema a multiplicada por 2.
-
La segunda ecuación del sistema b es la segunda ecuación del sistema a multiplicada por 3.
La solución de ambos sistemas es \(x = 1\) e \(y = 3\).
Apartado 2.
Si multiplicamos una ecuación por 0, ésta desaparece. Por ejemplo,
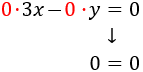
No podríamos resolver el sistema sin la ecuación (si solo teníamos 2 ecuaciones con 2 incógnitas); o la solución no sería correcta porque no cumpliría la ecuación omitida (si el sistema tiene más ecuaciones), salvo que la ecuación en cuestión sea linealmente dependiente de las otras.
Si multiplicamos una ecuación por una de las incógnitas, entonces la ecuación pasa a ser una ecuación totalmente distinta, puesto que estamos añadiendo soluciones.
Veamos un ejemplo sencillo: consideramos la ecuación
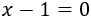
Esta ecuación tiene una única solución: \(x = 1\).
Si multiplicamos por \(x\), la ecuación queda
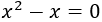
Y esta ecuación tiene dos soluciones: \(x = 0\) y \(x = 1\).
Hemos añadido una solución.
Conclusión: NO podemos multiplicar las ecuaciones por 0 ni por las incógnitas.
Problema 4 
Sin necesidad de resolver el siguiente sistema podemos afirmar que no tiene solución. ¿Sabrías decir por qué?
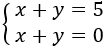
SOLUCIÓN:
Observemos la primera ecuación:
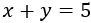
Podemos leerla como “los números \(x\) e \(y\) suman 5”.
Ahora observemos la segunda ecuación:
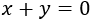
Podemos leerla como “los números \(x\) e \(y\) suman 0”.
Lógicamente, los números \(x\) e \(y\) pueden sumar 5, o pueden sumar 0, pero no pueden sumar 5 y 0 al mismo tiempo. Por tanto, dichos números no existen: el sistema no tiene solución.
En efecto, si operamos en la segunda ecuación tenemos
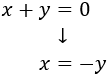
Sustituimos en la primera ecuación:
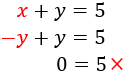
Obtenemos una igualdad falsa, un absurdo, que demuestra la inexistencia de solución del sistema.
Problema 5 
El siguiente sistema de ecuaciones tiene infinitas soluciones porque una de las dos ecuaciones es equivalente a la otra (la segunda ecuación se obtiene multiplicando la primera por 2):
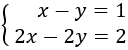
Se pide proporcionar 3 de las infinitas soluciones del sistema.
SOLUCIÓN:
La primera ecuación nos dice que “la diferencia entre los números \(x\) e \(y\) es 1”. Por tanto, todo par de números consecutivos \(x> y\) es una solución.
Por ejemplo, los números consecutivos \(x =2\) e \(y = 1\) son una solución del sistema:
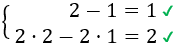
Los números consecutivos \(x =5\) e \(y = 4\) también son solución del sistema:
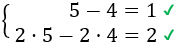
Los números consecutivos \(x =-1\) e \(y = -2\) también son solución del sistema:
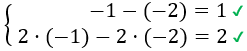
Podemos encontrar todas las soluciones que queramos siempre que se cumpla \( x = y+1\) (relación obtenida de la primera ecuación del sistema).
Sistema 12 
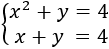
Resuelve por sustitución y comprueba la solución.
Resolvemos por SUSTITUCIÓN:
Como una de las incógnitas está al cuadrado, no se trata de un sistema de ecuaciones lineales. No obstante, podemos resolverlo por métodos básicos como el de sustitución.
Aislamos la \(y\) en la segunda ecuación para sustituirla en la primera:
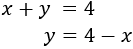
Sustituimos en la primera ecuación:
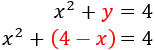
Tenemos una ecuación de segundo grado incompleta:
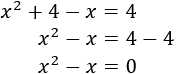
Para resolver estas ecuaciones tenemos que sacar factor común de la incógnita:
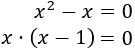
La ecuación tiene 2 soluciones y son \(x = 0\) y \(x = 1\).
Calculamos \(y\):
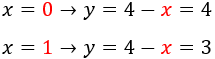
Una de las soluciones es \(x = 0\) e \(y = 4\). Comprobamos si verifica el sistema:
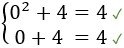
La otra solución es \(x = 1\) e \(y = 3\). Comprobamos:
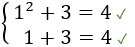
Por tanto, el sistema de ecuaciones tiene dos soluciones distintas: una es \(x = 0\) e \(y = 4\); y la otra es \(x=1\) e \(y = 3\).
Nota: observad que la solución es un par de números, pero no podemos mezclar dichos números. Por ejemplo, \(x = 0\) e \(y = 3\) (tomadas de la primera y la segunda solución) no es una solución del sistema.
Sistema 13 
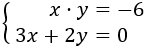
Resuelve por igualación.
Resolvemos por IGUALACIÓN:
La primera ecuación no es lineal porque las dos incógnitas se multiplican entre sí.
Aislamos, por ejemplo, la \(x\), en ambas ecuaciones para igualarlas:
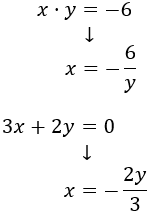
Igualamos y resolvemos:
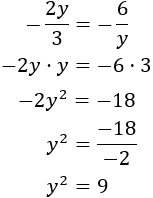
Para resolver esta ecuación de segundo grado solo tenemos que hacer la raíz cuadrada, pero no olvidemos el signo \(\pm\):
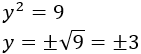
Calculamos la otra incógnita:
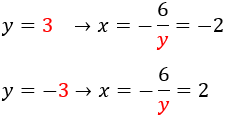
Por tanto, el sistema tiene dos soluciones. Una es \(x =-2\) e \(y = 3\); la otra es \(x =2\) e \(y = -3\).