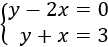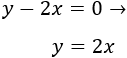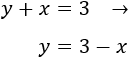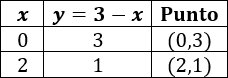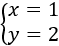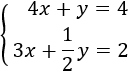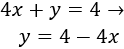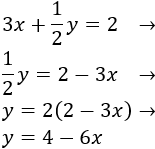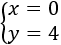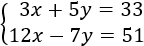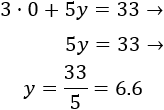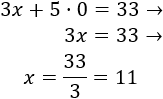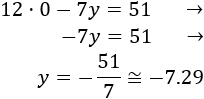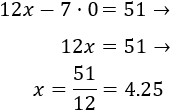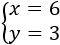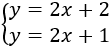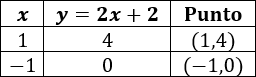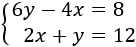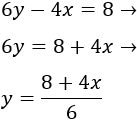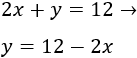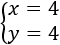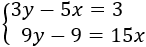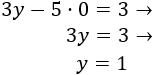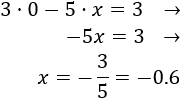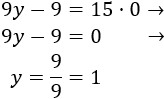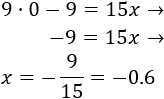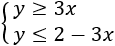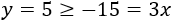Sistema 1 
Resolver gráficamente el siguiente sistema de ecuaciones:
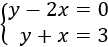
SOLUCIÓN:
Lo primero que hacemos es despejar la \(y\) en ambas ecuaciones para que sea más fácil calcular los puntos.
Primera ecuación:
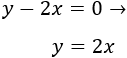
Segunda ecuación:
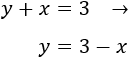
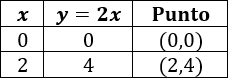
Ahora vamos a calcular unos cuantos puntos de las dos funciones para representarlas (con 2 es suficiente). Utilizaremos \(x = 0\) y \(x = 2\).
Para la primera función tenemos la tabla
Para la segunda función tenemos la tabla
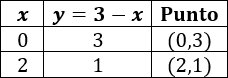
Ahora representamos los puntos de cada tabla y los unimos para obtener las rectas:
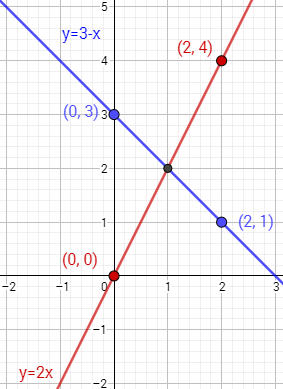
La solución del sistema es el punto donde las gráficas se cortan (intersección de la recta), es decir:
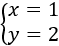
Sistema 2 
Resolver gráficamente el siguiente sistema de ecuaciones:
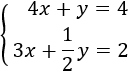
SOLUCIÓN:
Despejar la \(y\) en ambas ecuaciones.
Primera ecuación:
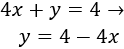
Segunda ecuación:
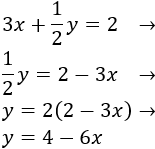
Ahora damos valores a \(x\) para obtener algunos puntos de cada recta. Utilizaremos \(x = 1\) y \(x = -1\).
Para la primera función tenemos la tabla

Para la segunda función tenemos la tabla

Representamos los puntos de cada tabla y los unimos:
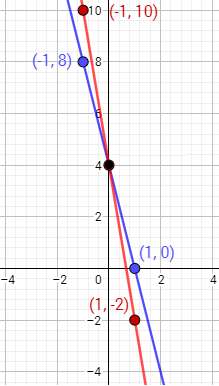
La solución del sistema es el punto de intersección, es decir,
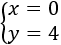
Sistema 3 
Resolver gráficamente el siguiente sistema de ecuaciones:
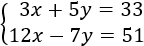
SOLUCIÓN:
En este problema vamos a dar valores a la \(x\) y a la \(y\) directamente (sin despejar la \(y\)). Los puntos que escogemos son los puntos de corte con los ejes (es decir, \(x = 0\) e \(y = 0\)).
En la primera ecuación, si \(x = 0\), entonces
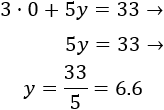
Y si \(y = 0\), entonces
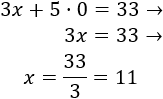
Por tanto, para la primera recta tenemos
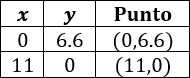
Repetimos el proceso con la segunda ecuación:
Si \(x = 0\), entonces
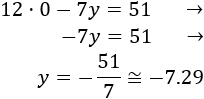
Y si \(y = 0\), entonces
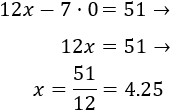
Por tanto, para la segunda recta tenemos
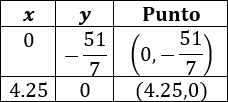
Representamos los 4 puntos y los unimos:
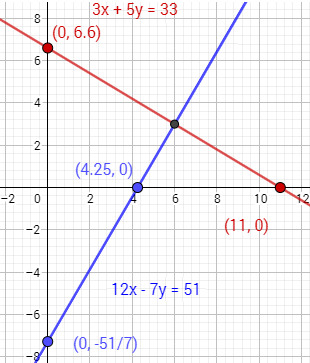
La solución del sistema es el punto de intersección de las gráficas de las rectas, esto es,
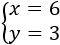
Sistema 4 
Resolver gráficamente el siguiente sistema de ecuaciones:
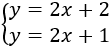
SOLUCIÓN:
Como tenemos la \(y\) despejada en ambas ecuaciones, damos valores a \(x\). Utilizamos \(x = 1\) y \(x = -1\).
Para la primera función tenemos la tabla
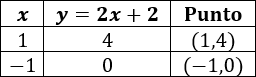
Para la segunda función tenemos la tabla

Ahora representamos los puntos de cada tabla y los unimos:
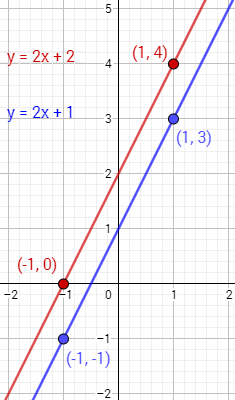
La solución del sistema es el punto donde las gráficas se cortan, pero las rectas de este problema no se cortan porque son paralelas (tienen la misma pendiente \(m = 2\)). Por tanto, el sistema no tiene solución.
Sistema 5 
Resolver gráficamente el siguiente sistema de ecuaciones:
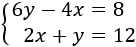
SOLUCIÓN:
Lo primero que hacemos es despejar la \(y\) en ambas ecuaciones.
Primera ecuación:
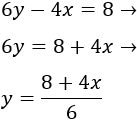
Segunda ecuación:
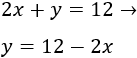
Ahora vamos a calcular unos cuantos puntos de las dos funciones para representarlas. Para la primera, utilizaremos \(x = -2\) y \(x = 10\) y para la segunda, \(x = 2\) y \(x = 6\).
La primera tabla que tenemos es

La segunda tabla es

Representamos y unimos los puntos de las rectas:
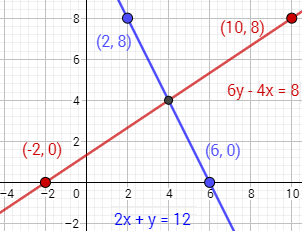
La solución del sistema es el punto donde las rectas se cortan:
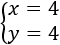
Sistema 6 
Resolver gráficamente el siguiente sistema de ecuaciones:
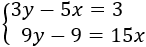
SOLUCIÓN:
En este problema vamos a dar valores a \(x\) y a \(y\) sin despejar la \(y\). Calcularemos los puntos de corte con los ejes dando los valores \(x = 0\) e \(y = 0\).
En la primera ecuación, si \(x = 0\), entonces
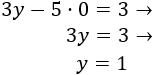
Y si \(y =0\), entonces
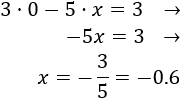
En la segunda ecuación, si \(x = 0\), entonces
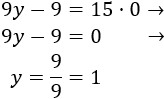
Y si \(y =0\), entonces
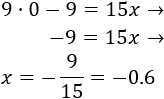
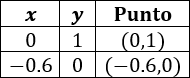
Para la primera función tenemos la tabla
Para la segunda función tenemos la tabla
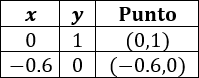
Los dos puntos obtenidos para cada función son iguales. Esto significa que las rectas se cortan en dos puntos y, por tanto, las ecuaciones representan la misma recta. Recordad que la intersección entre dos rectas puede ser:
-
un único punto,
-
ningún punto (las rectas son paralelas) o
-
infinitos puntos (se trata de la misma recta).
En este problema estamos en el tercer caso. Por tanto, el sistema de ecuaciones tiene infinitas soluciones.
La gráfica de las rectas del sistema es
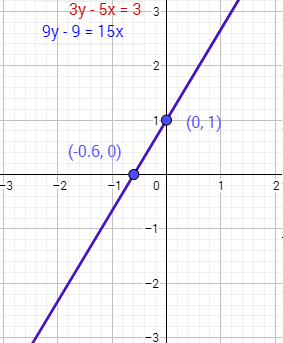
Nota 1: los puntos que son solución del sistema son los \((x,y)\) tales que \(3y-5x =3\).
Nota 2: si hubiésemos multiplicado toda la primera ecuación por 3 (operación que no cambia su gráfica) habríamos obtenido exactamente la segunda ecuación. Por esto mismo, las rectas son coincidentes: son ecuaciones equivalentes.
Sistema 7 
Resolver gráficamente el siguiente sistema de inecuaciones:
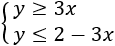
SOLUCIÓN:
En este problema tenemos dos desigualdades.
Cada una de las desigualdades representa una región del plano. La solución del sistema es la intersección de ambas regiones. Por tanto, lo que haremos es representar las dos regiones por separado para observar la región en la que se cortan.
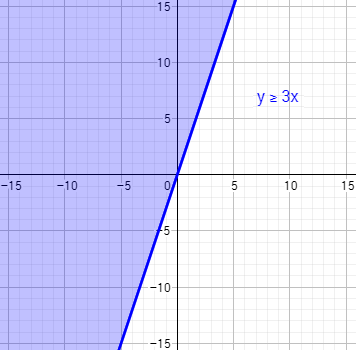
Para representar la región \( y\geq 3x\), representamos primero la recta \(y = 3x\). Podemos hacerlo dando puntos. La gráfica de la recta es
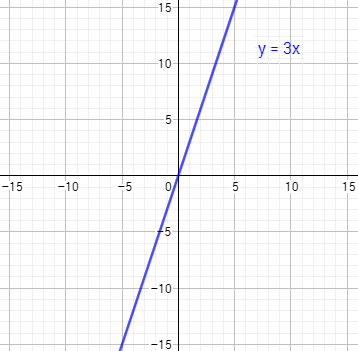
La recta divide el plano en dos regiones e \( y\geq 3x\) es una de ellas. Para saber cuál, tomamos un punto de cada una y comprobamos cuál de los dos cumple la desigualdad \( y\geq 3x\).
Tomamos los puntos (-5,5) (lado izquierdo) y (5,-5) (lado derecho):
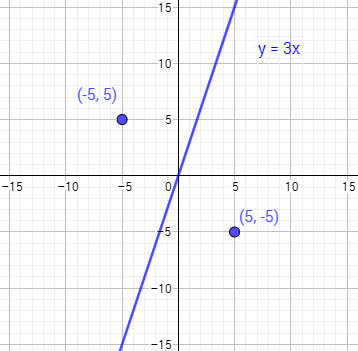
El punto que cumple la desigualdad \( y\geq 3x\) es el primero ya que
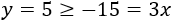
Por tanto, la región \( y\geq 3x\) es la del lado izquierdo (color azul):
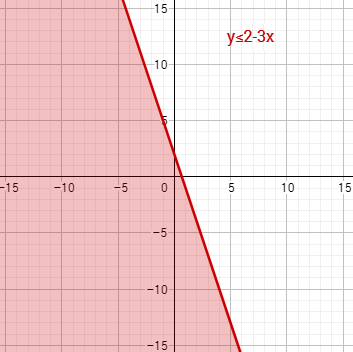
Repetimos el proceso con la región \(y \leq 2-3x\) (región roja):
Ahora representamos ambas regiones y su intersección (color más oscuro) es la solución del sistema:
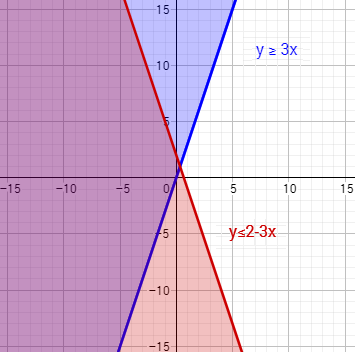
La solución del sistema de inecuaciones (o de desigualdades) es una región del plano y, por tanto, existen infinitos puntos que cumplen ambas inecuaciones.