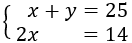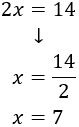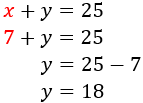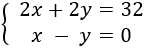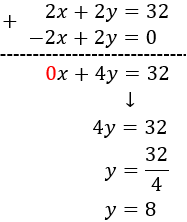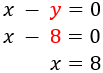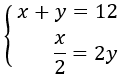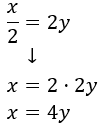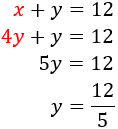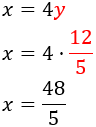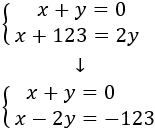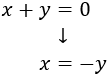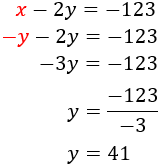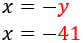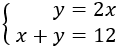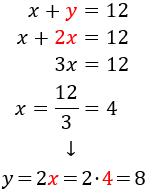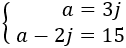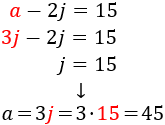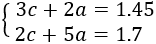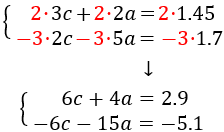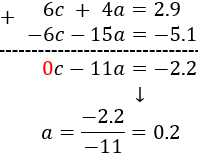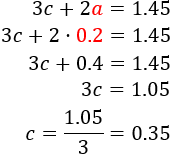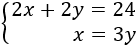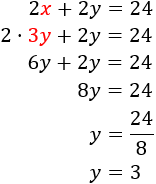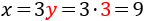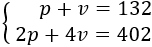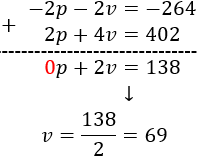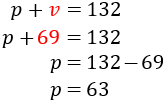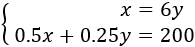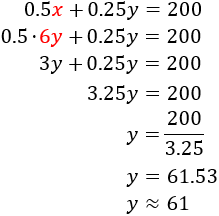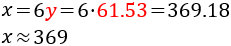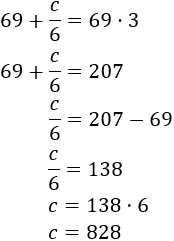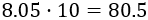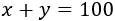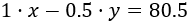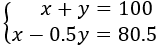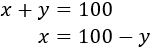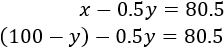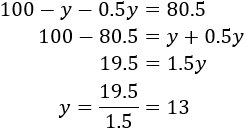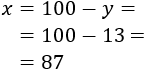Problema 1 
Dos números suman 25 y el doble de uno de ellos es 14. ¿Qué números son?
SOLUCIÓN:
En primer lugar, definimos las incógnitas:
-
\(x\) es uno de los números,
-
\(y\) es el otro número.
Por un lado, sabemos que los dos números suman 25, lo cual nos proporciona la primera ecuación:
$$ x + y = 25 $$
Por otro lado, también sabemos que el doble de uno de los números es 14, lo cual proporciona la segunda ecuación:
$$ 2x = 14 $$
Ya tenemos 2 incógnitas y 2 ecuaciones, suficiente para plantear y resolver el sistema de ecuaciones:
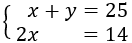
Aplicamos el método de sustitución, despejando la \(x\) en la segunda ecuación y sustituyendo en la primera.
Despejamos la \(x\) en la segunda ecuación:
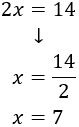
Observad que ya tenemos el valor de una incógnita: \(x = 7\).
Sustituimos en la primera ecuación (escribimos 7 en lugar de \(x\)) y resolvemos la ecuación:
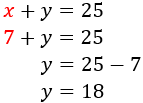
La solución del sistema es \(x = 7\) e \(y = 18\). Por tanto, los números buscados son 7 y 18.
Podemos comprobar el resultado:
-
Los dos números suman 25: $$ 7 + 18 = 25 $$
-
El doble de uno de ellos (7) es igual a 14: $$ 2\cdot 7 = 14 $$
Problema 2 
El doble de la suma de dos números es 32 y su diferencia es 0. ¿Qué números son?
SOLUCIÓN:
Llamaremos
-
\(x\) a uno de los números,
-
\(y\) al otro número.
Como el doble de la suma de los números es 32, tenemos la ecuación
$$ 2(x + y) = 32 $$
Nota: recordad que es importante escribir la suma de los números entre paréntesis.
Podemos quitar los paréntesis de la ecuación si multiplicamos por 2 los sumandos que contiene:
$$ 2(x + y) = 32 $$
$$ 2x + 2y = 32 $$
También, sabemos que la diferencia (la resta) de los números es 0:
$$ x - y = 0 $$
Nota: la anterior ecuación nos informa de que los números son iguales (\(x = y\)).
El sistema obtenido es el siguiente:
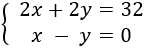
Para variar, resolvemos este sistema por el método de reducción.
Multiplicamos la segunda ecuación por -2 y sumamos las ecuaciones (desaparecerá la incógnita \(x\)):
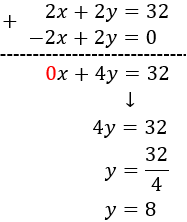
Finalmente, calculamos \(x\) sabiendo que \(y = 8\) usando la segunda ecuación:
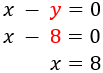
Por tanto, los números buscados son 8 y 8.
Podemos comprobar el resultado:
-
El doble de la suma de los números es 32: $$ 2\cdot (8 + 8) = 2\cdot 16 = 32 $$
-
La diferencia es 0: $$ 8 - 8 = 0$$
Problema 3 
La suma de dos números es 12 y la mitad de uno de ellos el doble del otro. ¿Qué números son?
SOLUCIÓN:
Definimos las incógnitas:
-
\(x\) es uno de los números,
-
\(y\) es el otro número.
La suma de los números es 12:
$$ x + y = 12 $$
La mitad del primer número es el doble del segundo:
$$ \frac{x}{2} = 2y $$
Tenemos el sistema de ecuaciones
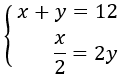
Resolvemos el sistema por sustitución.
Despejamos la \(x\) en la segunda ecuación:
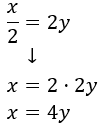
Sustituimos en la primera ecuación:
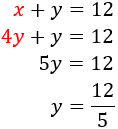
Como ya tenemos \(y\), podemos calcular \(x\):
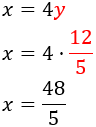
Por tanto, los números buscados son las fracciones 48/5 y 12/5.
Comprobamos el resultado (opcional):
-
Los números suman 12: $$ \frac{48}{5} + \frac{12}{5} = \frac{60}{5} = 12 $$
-
La mitad de 48/5 es $$ \frac{1}{2}\cdot \frac{48}{5} = \frac{24}{5} $$
-
El doble de 12/5 es $$ 2\cdot \frac{12}{5} = \frac{24}{5}$$
Problema 4 
Tenemos dos números cuya suma es 0 y si a uno de ellos le sumamos 123 obtenemos el doble del otro. ¿Qué números son?
SOLUCIÓN:
Sea \(x\) uno de los números y sea \(y\) el otro.
La suma de los números es 0:
$$ x + y = 0 $$
Si a uno de los números (por ejemplo, \(x\)) le sumamos 123 obtenemos el doble del otro número:
$$ x + 123 = 2y $$
Luego tenemos el sistema de ecuaciones
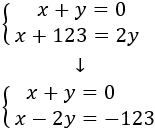
Nota: es mejor si escribimos las incógnitas en el lado izquierdo y los números en el derecho.
Resolvemos por sustitución.
Aislamos \(x\) en la primera ecuación:
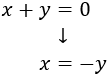
Sustituimos \(x = -y\) en la segunda ecuación:
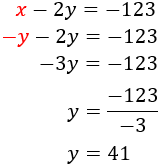
Calculamos la otra incógnita:
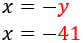
Por tanto, los números buscados son 41 y -41.
Podemos comprobar el resultado:
-
Sumando 123 a -41 obtenemos el doble de 41, que es 82: $$ -41 + 123 = 82 $$
-
La suma de los dos números es 0: $$ -41 + 41 = 0$$
Problema 5 
Hallar un número de dos cifras que cumpla:
- La segunda cifra es el doble de la primera
- La suma de las cifras es 12.
SOLUCIÓN:
A diferencia de los anteriores, en este problema tenemos que encontrar un único número.
El número que buscamos tiene 2 cifras, a las cuales llamaremos \(x\) e \(y\). Es decir, es el número \(xy\), siendo \(x\) la primera de sus cifras e \(y\) la segunda.
Importante: con \(xy\) nos referimos a un número de dos cifras y NO a la multiplicación \(x\cdot y\).
La segunda cifra es el doble de la primera:
$$ y = 2x $$
La suma de las cifras es 12:
$$x + y = 12$$
Tenemos un sistema de dos ecuaciones:
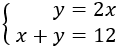
Resolvemos por sustitución (sustituyendo la primera ecuación en la segunda):
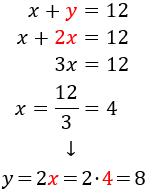
Por tanto, el número buscado es el 48 (la primera cifra es \(x = 4\) y la segunda es \(y = 8\)).
Comprobamos el resultado:
-
La segunda cifra es el doble de la primera: $$ 8 = 2\cdot 4 $$
-
Las cifras suman 12: $$ 4 + 8 = 12 $$
Nota: observad que también podemos resolver este problema sin plantear un sistema de ecuaciones. Los únicos números de dos cifras cuya segunda cifra es el doble de la primera son 12, 24, 36 y 48. Y el único número de éstos cuyas cifras suman 12 es el 48.
Problema 6 
Ana tiene el triple de edad que su hijo Jaime. Dentro de 15 años, la edad de Ana será el doble que la de su hijo. ¿Cuántos años tienen Ana y Jaime?
SOLUCIÓN:
En este problema usaremos otras incógnitas distintas a \(x\) e \(y\), lo cual no afectará a la resolución. A veces, usar otros nombres para las incógnitas puede ayudarnos a identificarlas, sobre todo cuando trabajamos con muchas.
Definimos las incógnitas:
-
Llamaremos \(a\) a la edad actual de Ana
-
y llamaremos \(j\) a la edad actual de Jaime.
La primera ecuación la obtenemos sabiendo que la edad de Ana es el triple que la de Jaime:
$$ a = 3j $$
Dentro de 15 años, tanto Ana como Jaime van a tener 15 años más, es decir,
-
La edad de Ana será \(a + 15\).
-
La edad de Jaime será \(j + 15\).
En este momento (pasados los 15 años), sabemos que la edad de Ana será el doble que la de Jaime:
$$ a + 15 = 2\cdot ( j + 15 )$$
Nota: no olvidemos el paréntesis para calcular el doble de la edad de Jaime.
Simplificamos la última ecuación:
$$ a + 15 = 2\cdot ( j + 15 )$$
$$ a + 15 = 2j + 2\cdot 15$$
$$ a + 15 = 2j + 30$$
$$ a -2j = 15$$
Tenemos, por tanto, el sistema de ecuaciones siguiente:
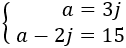
Resolvemos por sustitución:
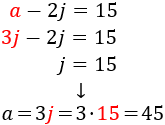
Ana tiene 45 años y su hijo Jaime tiene 15.
Comprobamos la solución (opcional):
-
La edad de Ana (45) es el triple que la de Jaime (15): $$ 45 = 3\cdot 15 $$
-
Dentro de 15 años, Ana tiene 60 años y Jaime tiene 30. En este momento, la edad de Ana es el doble que la de Jaime: $$ 60 = 2\cdot 30 $$
Problema 7 
Hemos comprado 3 canicas de cristal y 2 de acero por 1,45€ y, ayer, 2 de cristal y 5 de acero por 1,7€. Determinar el precio de una canica de cristal y de una de acero.
SOLUCIÓN:
Definimos las incógnitas del problema:
-
Sea \(c\) el precio de una canica de cristal
-
y sea \(a\) el precio de una canica de acero.
El precio de 3 canicas de cristal es \(3\cdot c\) y el precio de 2 canicas de acero es \(2\cdot a\). Sabemos que estas 3 canicas de cristal y 2 de acero valen, en total, 1.45€:
$$ 3c + 2a = 1.45 $$
Por otro lado, como 2 canicas de cristal y 5 de acero valen 1.7€,
$$ 2c + 5a = 1.7 $$
Tenemos el sistema de ecuaciones
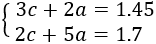
Resolvemos por reducción.
Vamos a eliminar la incógnita \(c\), que tiene coeficiente 3 (primera ecuación) y coeficiente 2 (segunda ecuación). Para que se anulen al sumar las ecuaciones, multiplicamos la primera ecuación por 2 y la segunda por -3:
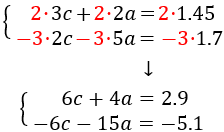
Sumamos las ecuaciones del sistema:
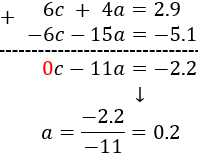
Calculamos la otra incógnita a partir de la primera ecuación y \(a\):
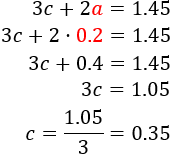
Una canica de acero vale 0.2€ y una de cristal 0.35€.
Problema 8 
Hallar la longitud de los lados de un rectángulo cuyo perímetro es P = 24 y cuyo lado mayor mide el triple que su lado menor. ¿Cuál es el área del rectángulo?
SOLUCIÓN:
Los rectángulos constan de cuatro lados: dos lados paralelos iguales (base) y otros dos lados paralelos iguales (altura).
Incógnitas:
-
Llamamos \(x\) al lado mayor del rectángulo.
-
Llamamos \(y\) al lado menor del rectángulo.
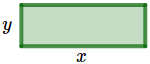
El perímetro \(P\) es la suma de los 4 lados del rectángulo:
$$P = x + x + y + y $$
Es decir,
$$P = 2x + 2y $$
Como sabemos que el perímetro es 24, tenemos la ecuación
$$2x + 2y = 24$$
Como el lado mayor mide tres veces el menor:
$$ x = 3y$$
Luego tenemos el sistema de ecuaciones
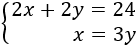
Resolvemos por sustitución (sustituimos \(x = 3y\) en la primera ecuación):
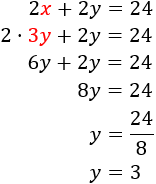
Calculamos la otra incógnita sustituyendo en la segunda ecuación:
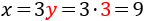
Los lados mayores miden 9 unidades y los menores miden 3 unidades (cada uno de ellos).
El área del rectángulo se calcula multiplicando su base por su altura:
$$ A = x\cdot y = 9\cdot 3 = 27$$
Problema 9 
Averiguar el número de animales de una granja sabiendo que:
- la suma de patos y vacas es 132 y la de sus patas es 402.
- se necesitan 200kg al día para alimentar a las gallinas y a los gallos. Se tiene un gallo por cada 6 gallinas y se sabe que una gallina come una media de 500g, el doble que un gallo.
- se piensa que la sexta parte de los conejos escapan al comedero de las vacas, lo que supone el triple de animales en dicho comedero.
SOLUCIÓN:
Apartado 1
Hay que tener en cuenta que cada pato tiene 2 patas y cada vaca 4.
Incógnitas (usaremos las iniciales):
-
Llamamos \(p\) al número de patos
-
Llamamos \(v\) al número de vacas
La suma de los patos y vacas es 132:
$$ p + v = 132 $$
La suma de las patas es 402 (dos patas por cada pato y cuatro por cada vaca):
$$ 2p + 4v = 402 $$
Tenemos el sistema de ecuaciones
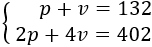
Resolvemos por reducción.
Multiplicamos la primera ecuación por -2 para eliminar la incógnita \(p\) al sumar las ecuaciones:
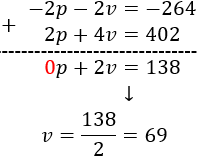
Calculamos la otra incógnita:
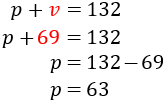
Por tanto, hay 63 patos y 69 vacas.
Apartado 2
Como las cantidades de pienso que consumen son aproximadas, no obtendremos el número exacto de animales, sólo una estimación.
Incógnitas (usaremos x e y por los cromosomas sexuales):
-
Llamamos \(y\) al número de gallos
-
Llamamos \(x\) al número de gallinas
Como hay un gallo por cada 6 gallinas, el número de gallinas es 6 veces el de gallos:
$$ x = 6y $$
Una gallina come 0.5kg y un gallo 0.25kg. En total consumen 200kg:
$$ 0.5x + 0.25y = 200$$
Nota: en el enunciado del problema se indica que el total son 200kg, pero las cantidades que comen las gallinas y gallos es en gramos. Por eso, al pasar de gramos a kilogramos obtenemos decimales.
Tenemos el sistema de ecuaciones
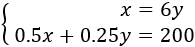
Aplicamos el método de sustitución (sustituimos \(x = 6y\) en la segunda ecuación):
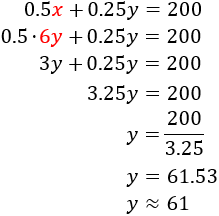
Como obtenemos un número decimal, podemos aproximar el número de gallos a 61, pero usaremos el resultado decimal para calcular el número de gallinas y obtener un resultado más real:
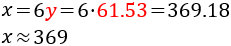
Podemos decir que hay unos 61 gallos y unas 369 gallinas.
Apartado 3
Ya sabemos que hay 69 vacas (apartado 1).
Sea \(c\) el número de conejos.
La sexta parte de conejos está junto a las vacas, por lo que el número de animales que hay en el comedero de las vacas es: número total de vacas más la sexta parte del número total de conejos:
$$ 69 + \frac{c}{6} $$
Al contar los conejos y las vacas, el número de animales en el comedero de las vacas es el triple del que debería ser (debería ser 69, que es el número de vacas):
$$ 69 + c/6 = 69\cdot 3 $$
Resolvemos la ecuación de primer grado:
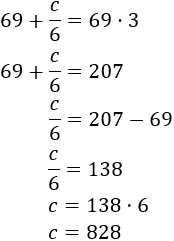
Hay 828 conejos en total (de los cuales 138 están en el comedero de las vacas).
Resumiendo:
-
Patos: 63.
-
Vacas: 69.
-
Gallos: 61 (aproximadamente).
-
Gallinas: 369 (aproximadamente).
-
Conejos: 828.
Problema 10 
En un examen tipo test, las preguntas correctas
suman un punto y las incorrectas restan medio punto.
En total hay 100 preguntas y no se admiten respuestas
en blanco (hay que contestar todas).
La nota de un alumno es 8.05 sobre 10. Calcular el número
de preguntas que contestó correcta e incorrectamente.
SOLUCIÓN:
Escribimos la nota sobre 100 en vez de sobre 10:
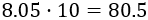
Llamamos \(x\) al número de respuestas correctas e \(y\) al número de respuestas
incorrectas.
Como se deben contestar todas las preguntas, debe cumplirse que el número de respuestas correctas más el de respuestas incorrectas es igual a 100:
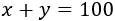
Cada respuesta correcta suma 1 y cada incorrecta resta 0.5:
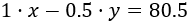
Luego tenemos el sistema
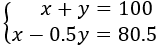
Resolvemos el sistema de ecuaciones por sustitución.
Aislamos la \(x\) en la primera ecuación:
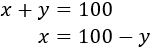
Sustituimos \(x\) en la segunda ecuación:
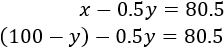
Resolvemos la ecuación de primer grado:
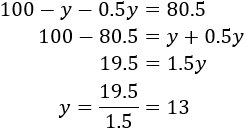
Tenemos que el número de respuestas incorrectas es \(y = 13\).
Fácilmente calculamos el número de respuestas correctas:
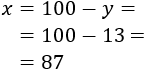
Problema 11 
Si se suma 7 al numerador y al denominador de una determinada fracción, se obtiene
la fracción
$$ \frac{2}{3} $$
Si en vez de sumar 7 se resta 3 al numerador y al denominador, se obtiene la
fracción
$$ \frac{1}{4} $$
Encontrar dicha fracción.
SOLUCIÓN:
Podemos llamar \(x\) al numerador e \(y\) al denominador. Es decir, la fracción que buscamos es
$$ \frac{x}{y} $$
Si sumamos 7 al numerador y al denominador y obtenemos 2/3:
$$ \frac{x+7}{y+7} = \frac{2}{3} $$
Podemos pasar los denominadores multiplicando al otro lado de la igualdad:
$$ 3(x+7) = 2(y+7) $$
Operamos un poco para simplificar la ecuación:
$$ 3x+21 = 2y+14 $$
$$ 3x -2y = -7 $$
Ahora procedemos del mismo modo pero restando 3:
$$ \frac{x-3}{y-3} = \frac{1}{4} $$
Operamos un poco:
$$ 4(x-3) = y-3 $$
$$ 4x-12 = y-3 $$
$$ 4x-y = 9 $$
Por tanto, el sistema de ecuaciones lineales es
$$ 3x -2y = -7 $$
$$ 4x-y = 9 $$
Lo resolvemos por igualación, aislando en ambas ecuaciones la \(x\).
De la primera ecuación,
$$ 3x -2y = -7 $$
$$ x = \frac{-7+2y}{3} $$
Y de la segunda,
$$ 4x-y = 9 $$
$$ x = \frac{9+y}{4} $$
Igualamos las \(x\):
$$ \frac{-7+2y}{3} = \frac{9+y}{4}$$
Resolvemos la ecuación de primer grado:
$$ 4(-7+2y) = 3(9+y)$$
$$ -28+8y = 27 + 3y $$
$$ 5y = 55 $$
$$ y = \frac{55}{5} = 11 $$
Calculamos \(x\) a partir de la \(y\):
$$ x = \frac{-7+2y}{3} =$$
$$ x = \frac{-7+22}{3} =$$
$$ x = \frac{15}{3} =$$
$$ x = 5 $$
Por tanto, la fracción buscada es
$$ \frac{x}{y} = \frac{5}{11} $$
Problema 12 
Una marca de bebidas prepara una limonada (agua y concentrado de limón) con una
cantidad muy precisa de sus ingredientes.
La relación entre las cantidades de agua y concentrado limón es
$$ L_L = \frac{2 L_A}{5} $$
donde LL representa los litros de concentrado de limón y
LA los litros de agua.
Si se necesitan 20 limones para obtener un litro de concentrado de limón, ¿cuántos limones
se necesitan para elaborar 1230 botellas de 2L de esta limonada?
SOLUCIÓN:
Las 1230 botellas de 2L equivalen a un total de \(1230\cdot 2 = 2460\) litros de limonada.
Siguiendo la notación del propio problema, definimos las incógnitas siguientes:
-
\(L_L\) son los litros de concentrado de limón
-
\(L_A\) son los litros de agua
Una de las ecuaciones del sistema es la proporcionada por el enunciado:
$$ L_L = \frac{2 L_A}{5} $$
La otra es la siguiente:
$$ L_L + L_A = 2460 $$
Es decir, el total de litros de limonada es la suma de los litros de agua y de los litros
de concentrado de limón.
Resolvemos el sistema por sustitución:
De la segunda ecuación despejamos \(L_L\):
$$ L_L = 2460 - L_A $$
Sustituimos \(L_L\) en la primera ecuación:
$$ L_L = \frac{2 L_A}{5} $$
$$ 2460 - L_A = \frac{2 L_A}{5} $$
Resolvemos la ecuación de primer grado obtenida:
$$ 5\cdot 2460 - 5L_A = 2L_A $$
$$ 12300 = 5L_A + 2L_A $$
$$ 12300 = 7L_A $$
$$ L_A = \frac{12300}{7} = 1757.14\text{ L} $$
Nota: la \(\text{L}\) anterior indica litros, no tiene que ver con el nombre de las
incógnitas.
Ahora, calculamos los litros de concentrado de limón:
$$ L_L = 2460 - 1757.14 = 702.86L $$
Como se requieren 20 limones para un litro de concentrado y queremos
702.86L de concentrado, necesitamos
$$ 20\cdot 702.86 = 14057.2 $$
Es decir, se necesitan 14058 limones.
Problema 13 
Con una cuerda de 34 metros se puede dibujar un rectángulo (sin que sobre cuerda) cuya diagonal mide 13 metros.

Calcular cuánto mide la base y la altura de dicho rectángulo.
SOLUCIÓN:
Incógnitas:
-
\(b\) es la base del rectángulo
-
\(a\) es la altura del rectángulo
La longitud de la cuerda coincide con el perímetro del rectángulo (\(P = 2a + 2b\)), por lo que
$$ 2a + 2b = 34 $$
Si dibujamos la diagonal del rectángulo veremos 2 triángulos rectángulos, siendo
su hipotenusa la diagonal del rectángulo:
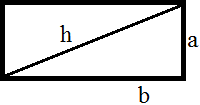
Aplicamos el Teorema de Pitágoras:
$$ a^2 + b^2 = h^2 $$
donde \(h\) representa la hipotenusa (la diagonal del rectángulo), que sabemos que mide 13. Luego
$$ a^2 + b^2 = 13^2 = 169 $$
La dificultad del problema se debe a esta última ecuación ya que no es lineal (las incógnitas
están al cuadrado).
Aislamos \(a\) en la primera de las ecuaciones:
$$ 2a + 2b = 34 $$
$$ a = \frac{34-2b}{2} = 17-b$$
Ahora sustituimos \(a\) en la ecuación no lineal:
$$ a^2 + b^2 = 169 $$
$$ (17-b)^2 + b^2 = 169 $$
Calculamos el cuadrado de la resta (binomio de Newton):
$$ (17-b)^2 = 17^2 +b^2 -2\cdot 17b =$$
$$ = 289 +b^2 -34b $$
Por tanto, tenemos una ecuación de segundo grado:
$$ 289 +b^2 -34b + b^2 = 169 $$
Simplificamos un poco:
$$ 2b^2 -34b +120 =0 $$
Omitimos el procedimiento ya que no pertenece al tema de sistemas de ecuaciones. Las soluciones son:
$$ b=12,\ b=5 $$
Por lo que \(a\) puede tener dos valores:
$$ a = 17-b = 17-5=12 $$
$$ a = 17-b = 17-12=5 $$
Nota: en realidad sólo existe una solución al problema ya que si \(b = 12\), entonces \(a = 5\) y si \(b = 5\) entonces \(a = 12\). Esto se debe a que no importa si consideramos un lado como la base o como la altura.
Por tanto, los lados del rectángulo miden 12 y 5 metros.
Problema 14 
En un concierto benéfico se venden todas las entradas y se recaudan 23 mil dólares. Los precios de las entradas son 50 dólares las normales y 300 dólares las vip.
Calcular el número de entradas vendidas de cada tipo si el aforo del establecimiento es de 160 personas.
SOLUCIÓN:
Definimos las incógnitas del sistema:
-
\(v\) es el número de entradas vip
-
\(n\) es el número de entradas normales
El número total de entradas coincide con el número total de personas:
$$ v + n = 160 $$
La recaudación es
$$ 300v + 50n = 23000 $$
Resolvemos el sistema de ecuaciones por igualación (aislamos \(v\) en ambas
ecuaciones):
De la primera ecuación:
$$ v = 160-n $$
De la segunda ecuación:
$$ v = \frac{23000 - 50n}{300} $$
Igualamos ambas expresiones:
$$ 160-n = \frac{23000 - 50n}{300} $$
La solución de la ecuación de primer grado anterior es:
$$ n = 100 $$
Por tanto,
$$ v = 160-100 = 60 $$
Por tanto, se vendieron 60 entradas vip y 100 normales.
Problema 15 
Un niño realiza las siguientes observaciones sobre un parque
infantil de pelotas:
- Hay pelotas verdes, rojas y amarillas.
- El número total de pelotas verdes y el de pelotas rojas suman cinco veces el número de las amarillas.
- El número de pelotas verdes es el triple que el de amarillas.
- El número de pelotas amarillas y el de rojas suman 123.
SOLUCIÓN:
Llamaremos \(v\) al número de pelotas verdes, \(r\) al número de pelotas rojas y \(a\) al número de pelotas amarillas.
El segundo punto nos dice que
$$ v+r = 5a $$
El tercer punto nos dice que
$$ v = 3a $$
Y el cuarto nos dice que
$$ a+r = 123 $$
Tenemos un sistema de 3 ecuaciones lineales con 3 incógnitas.
Resolvemos el sistema por sustitución:
Sustituimos la \(v\) de la segunda ecuación en la primera ecuación:
$$ v+r = 5a $$
$$ 3a+r = 5a $$
Aislamos \(r\):
$$ r = 5a -3a $$
$$ r = 2a $$
Sustituimos \(r\) en la tercera ecuación:
$$ a+r = 123 $$
$$ a+2a = 123 $$
$$ 3a = 123 $$
$$ a = 41 $$
Ahora usamos el valor de \(a\) para obtener las otras incógnitas:
$$ r = 2a = 82 $$
$$ v = 3a = 123 $$
Por tanto, el número de pelotas de cada color es
-
Verdes: 123
-
Rojas: 82
-
Amarillas: 41
Problema 16  (sin plantear un sistema de ecuaciones)
(sin plantear un sistema de ecuaciones)
Calcular el número de números positivos de 3 cifras (mayores que 99 y menores que 1000) tales que
una de sus cifras es 0 y las otras dos cifras suman 7.
SOLUCIÓN:
Como los números son de 3 cifras (siendo una de ellas 0), serán de la forma \(xy0\), o bien, \(x0y\). Las incógnitas \(x\) e \(y\) pueden ser los números 1, 2, 3, 4, 5, 6, 7 y, además, \(y\) puede ser 0.
Nota: los números \(0xy\) no son de tres cifras ya que en realidad lo serían de dos: \(xy\) (menores que 100).
Nota 2: los números \(x\) e \(y\) no pueden ser 8 ni 9 porque entonces su suma sería mayor que 7.
En ambos casos, tiene que cumplirse que las cifras suman 7:
$$ x+y = 7 $$
Por tanto, tenemos las posibilidades siguientes:
| x |
y |
x + y |
xy0 |
x0y |
| 1 |
6 |
7 |
160 |
106 |
| 2 |
5 |
7 |
250 |
205 |
| 3 |
4 |
7 |
340 |
304 |
| 4 |
3 |
7 |
430 |
403 |
| 5 |
2 |
7 |
520 |
502 |
| 6 |
1 |
7 |
610 |
601 |
| 7 |
0 |
7 |
700 |
700 |
Nota: \(x\) no puede ser 0 ya que es la primera cifra en ambos casos. Sin embargo, \(y\) sí puede ser 0 por ser la segunda o tercera cifra.
En la tabla se recogen las 7 posibilidades y son válidas para ambos casos, excepto la última, que proporciona el mismo número en la forma \(xy0 = 700\) y \(x0y = 700\).
Por tanto, hay un total de 13 números.
Más problemas: 10 problemas de sistemas explicados.