Construcción de Autómatas Finitos
|
Contenido de esta página:
Introducción
En esta sección vamos a ver cómo
construir autómatas finitos (deterministas y no deterministas y con y
sin pila) a partir de expresiones regulares o de la
propia definición
del lenguaje.
Recordamos al lector que las expresiones regulares
son una forma de representar un lenguaje (regular). Veamos algunos ejemplos:
0(11)*
El lenguaje de esta expresión regular lo conforman las
palabras que empiezan por 0 seguidas de un número par de 1's (el
asterisco significa que la subcadena a la que enierra puede repetirse
tantas veces como se desee).
La palabra w = 0 también es una palabra de dicho lenguaje y corresponde al caso en que la subcadena 11 se
repite 0 veces.
(1+0)1*
El lenguaje está formado por las palabras que empiezan por 0 o por 1 (el signo
+ representa la unión, es decir, o uno u otro) y que están seguidas (o no) por
1's.
(000)*
Representa el lenguaje formado por las cadenas con
un número múltiplo de 3 de ceros.
La palabra vacía, ε, también forma parte de este lenguaje.
También podemos escribir este lenguaje como
$$ L = \{ 0^{3n} : n \geq 0,\ n \in \mathbb{N} \}$$
-
L = { 1 n 0 m : n, m ≥ 0 naturales}
Este lenguaje también puede expresarse mediante la expresión
regular 0*1*. Sin embargo, si exigimos que n = m ya no es posible
expresarlo mediante una expresión regular ya que dicho lenguaje no es regular. Es un lenguaje libre del contexto.
Páginas relacionadas:
Problemas resueltos
PROBLEMA 1
Dado el alfabeto
$$ \Sigma = \{ 0,1 \}$$
construir un Autómata Finito Determinista de 4 estados
como máximo, que acepte el lenguaje representado por la siguiente
expresión regular
$$((01 + 10)(11)^* 0)^*(01+10)(11)^*$$
Ver solución
Vamos a representar el autómata por partes, es decir,
iremos obteniendo autómatas hasta llegar al autómata final que se pide.
El primer autómata que vamos a escribir es de cuatro estados y
acepta el siguiente lenguaje
$$(01 + 10)$$
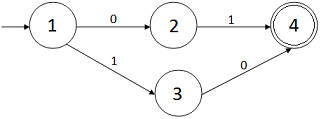
No hacemos ningún comentario ya que el autómata es simple.
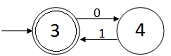
Ahora vamos a añadir las cadenas (11)*,
es decir, el siguiente autómata acepta el lenguaje
$$(01 + 10 )(11)^*$$
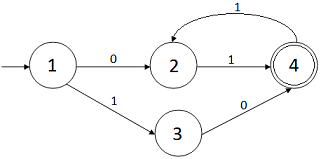
Hemos añadido sólo un arco etiquetado
con 1 del estado 4 (el final) al estado 2.
Veamos su funcionamiento:
como el arco empieza en el estado final, cabe
la posibilidad de no usarse, es decir, lo que corresponde
con el elemento
$$\varepsilon \ de\ (11)^*$$
-
que el arco acabe en el estado 2 asegura que una vez se accede
al arco, necesariamente tiene que haber otro 1 para poder alcanzar
el estado final, es decir, este arco sirve para concatenar
la palabra 11,
El siguiente paso es el lenguaje
$$((01 + 10 )(11)^*0)^*$$
Queremos que todas las palabras anteriores terminen con un 0
y, además, la expresión está encerrada bajo un *,
por lo que tendrá que haber un arco al estado inicial de modo que
exista la posibilidad de recorrer el autómata tantas veces como
se desee.
Está claro que el arco etiquetado con 0 tiene que comenzar
en el estado 4. Nos vemos obligados a cambiar el estado final
ya que, hasta ahora, no todas las palabras acaban en 0
(sólo la palabra 10). Así pues, el estado final
actual será el estado inicial anterior:
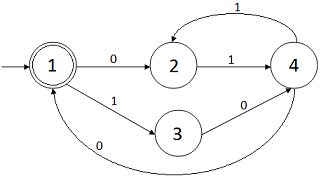
Observaciones:
En el siguiente paso vamos a concatenar las palabras del
lenguaje
$$(01+10)(11)*$$
a las que ya teníamos anteriormente. Como la expresión
anterior la hemos obtenido, en realidad, en el primer
diagrama, será suficiente cambiar el estado final al estado 4:
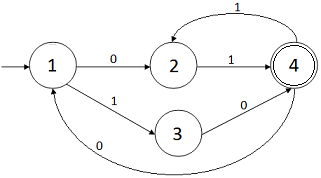
Observaciones: si llamamos
$$ a = (01+10)(11)^*$$
el lenguaje que queremos representar es
$$(a0)^*a $$
De este modo,
si sólo se accede al
estado 4 (estado final) una vez, la palabra es de la forma a
si se accede n + 1 veces al estado 4,
la palabra es de la forma
$$(a0)_1(a0)_2...(a0)_n a0$$
donde el subíndice de cada paréntesis indica
el número de veces que se repite la secuencia a0.
Por tanto, se trata de una palabra del lenguaje.
Tabla de la función de transición del AFD:
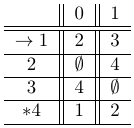
PROBLEMA 2
Dado el alfabeto Σ = { a, b, c }, definir un Autómata Finito Determinista
para el lenguaje formado por las cadenas x tales que nα (x)
es par y no existe ninguna subcadena bc en x.
nα (x) representa el número de a's en la cadena x. Consideramos que el número 0 es un
número par.
Ver solución
Tenemos dos condiciones para el estado final: n α (x) par y que no
haya subcadenas bc en x. Primero vamos a tratar la primera condición:
Definimos dos estados: q = 1 que es el inicial y también el final y
q = 2. Estaremos en el primero cuando n α (x)
es par y en el segundo cuando es impar. Comenzamos en q = 1 ya que no tenemos ninguna
a. Cambiaremos al otro estado cuando haya otra a. Si tenemos otra a,
volveremos al primer estado.
Veamos el diagrama de este autómata que posteriormente
modificaremos:
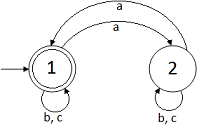
Este autómata controla la paridad de a's pero no discrimina
si existen o no subcadenas bc.
Esto es lo que vamos a hacer ahora definiendo otros dos estados.
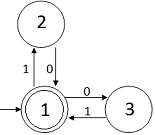
Mostramos el diagrama del autómata propuesto y después lo
explicaremos:
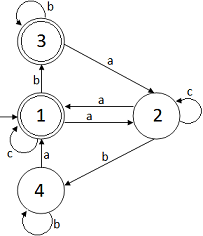
El autómata es finito y determinista.
Los transiciones directas que hay entre los estados
1 y 2 se producen cuando se encuentra un
símbolo a en la palabra.
El primero corresponde a n α (x) par y
el segundo a n α (x) impar.
Por ello, el primer estado es un estado final.
En el estado 1 hay un arco saliente y entrante con
la etiqueta c.
Esto se debe a que las c's pueden aparecer concatenadas
o detrás de una a.
-
No sucede lo mismo que en el punto anterior con las b's ya que éstas
no pueden estar seguidas de una c.
Por ello, cuando aparece una b (ya sea detrás de una a
o de una c se accede a un estado distinto para asegurar
que posteriormente no haya ninguna otra c.
Este estado del que hablamos son en realidad dos: el estado
3 y el estado 4. Al estado 3 se accede desde el estado 1
(en el que n α (x) es par) por lo que es
un estado final (n α (x) sigue siendo par).
Al estado 4 se accede cuando n α (x) es impar,
por lo que no puede ser un estado final.
Los estados 3 y 4 (cuando hay una b) no tienen
arcos etiquetados con c para evitar la subcadena bc,
pero sí tiene etiquetas a.
Según si en el estado actual n α (x)
es par o no, se accede a los estados 1 ó 2 a través de un arco
etiquetado con a.
Los estados 3 y 4 tienen una etiqueta
b saliente y entrante ya que las b's pueden
concatenarse.
Tabla de la funcón de transición del AFD:
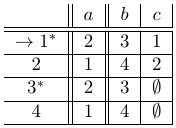
PROBLEMA 3
Dado el alfabeto Σ = { 0, 1 },
construir un Autómata Finito que acepte el siguiente lenguaje:
Si la cadena no tiene ningún 1, entonces la cadena debe
contener un número de par de 0's (consideramos al cero como par);
si la cadena tiene un número par de 1's (y mayor que 0 ),
la cadena debe terminar con un número impar de 0's;
si la cadena tiene un número impar de 1's, la cadena debe
terminar con un número par de 0's.
Ver solución
Lo primero que haremos es diferenciar entre número par o
impar de 1's en la palabra. Para ello dispondremos de dos
estados: q = 2 si es par y q = 3 si es impar.
Estos dos estados están unidos por dos
arcos etiquetados con 1 ya que cada vez que aparece un nuevo 1 en la
palabra cambia la paridad.
Para los 0's vamos a utilizar un estado distinto para cada uno
de los estados q = 2 y q = 3:
el estado q = 1 para q = 2 y el estado q =5
para q = 3.
El diagrama es el siguiente (no es el final):
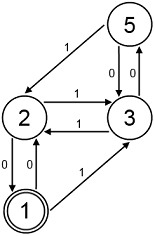
Observaciones:
-
Notemos que de cada uno de estos dos estados
(es decir, q = 1 y q = 5) parte
también un arco
etiquetado con 1 que nos conduce al estado opuesto del que venimos
mediante el arco etiquetado con 0.
Es decir, si
estamos en q = 1
(desde q = 2) nos lleva a q = 3;
si estamos en q = 5, nos lleva a q = 2.
Esto lo hacemos así porque los estados 1 y 5 tienen
memoria de
paridad de unos. Luego al aparecer un 1 tenemos que
cambiar de paridad.
-
El estado 1 es un estado final ya que sólo se accede
a él después de un número impar de 0's (bucle 2 <····> 1)
y esto sólo ocurre el caso de número par de 1's.
El diagrama final del autómata es el siguiente:
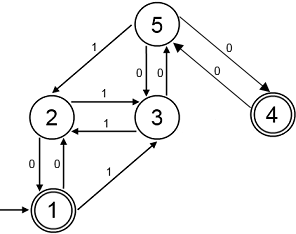
Observaciones:
-
Lo que nos permite el estado 4 es asegurar
que las palabras que tienen un número impar de 1's terminen
con una secuencia par de 0's (entrando en el bucle
5 <···> 4).
Notemos que sólo accedemos a este estado cuando ya no
habrá más 1's en la palabra.
-
El estado 1 es el inicial. No hemos hablado de la primera
de las condiciones (que si no hay 1's en la palabra,
el número de 0's es par),
pero este caso consiste en el bucle de
estados 1 <····> 2.
El autómata no es determinista ya que
en algunos estados tenemos arcos salientes con la misma
etiqueta pero que terminan en distintos estados.
La tabla de la función de transición es:
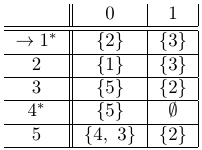
PROBLEMA 4
Dado el alfabeto Σ = { 0, 1 }, considerar
los siguientes lenguajes:
$$ L_1 = \{ (01)^n\ | n \geq 0 \} $$
$$ L_2 = \{ (10)^n\ | n\geq 0 \} $$
$$ L_2 = L_3 = L_1 \cup L_2 $$
Ver solución
Construir el autómata finito que reconozca el
lenguaje
$$ L = L_3^* $$
Consideremos el siguiente autómata:
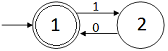
Es fácil ver que acepta el lenguaje L 1.
Igualmente, el siguiente autómata acepta el lenguaje
L 2:
Sabemos que dado un lenguaje L, por definición,
$$ L^* := \cup _{i\in \mathbb{N}}\ L^i $$
Es fácil ver que las palabras de L12
son de la forma
$$ (10)^n (10)^m,\ $n,m\geq 0 $$
Pero
$$(10)^n (10)^m = (10)^{(n+m)}$$
y éste es un elemento de L1. Es decir,
podemos probar fácilmente por inducción que
$$ L_1 ^* = L_1$$
Sucede lo mismo con el otro lenguaje:
$$ L_2 ^* = L_2 $$
Buscamos un autómata para el lenguaje
$$ L = L_3 ^* = (L_1 \cup L_2) ^* $$
Vamos a ver cómo son sus palabras:
$$ L_3 ^1 = (L_1 \cup L_2) = \{ (10)^n,\ (01)^m\ |\ n,m\in \mathbb{N} \}$$
$$L_3 ^2 = (L_1 \cup L_2)(L_1 \cup L_2) = \{ (10)^t,\ (10)^m(01)^n, \ (01)^r(10)^s,\ (01)^u\ |\ t,m,n,r,s,u \in \mathbb{N} \}$$
Hemos tenido en cuenta que
$$ (10)^n (10)^m = (10)^{(n+m)},\ n,m\geq 0$$
Además, podemos escribir
$$ (10)^t = (10)^t(01)^0 $$
para simplificar más.
Análogamente para (01)u:
$$L_3 ^2 = \{ (10)^m(01)^n, \ (01)^r(10)^s\ |\ m,n,r,s \in \mathbb{N} \}$$
$$L_3 ^3 = \{ (10)^m(01)^n(10)^u, \ (01)^q(10)^r(01)^s\ |\ m,n,u,p,r,s \in \mathbb{N} \}$$
Podemos deducir que el lenguaje L3*
estará constituido por palabras formadas por la
concatenación alternada o no de (10) y/o (01), es decir,
$$ L_3^* = ((10)^* (01)^*)^*$$
Este lenguaje es aceptado por el siguiente autómata (finito determinista):
PROBLEMA 5
Dado el alfabeto Σ = { 0, 1 }$, construir el
Autómata Finito Determinista equivalente a la siguiente expresión:
$$ (((0 + 10)(10)^*(11 + 0)) + 11)(0 + 1)^*$$
Ver solución
Iremos construyendo el autómata paso a paso.
Para la expresión regular (0+10) tenemos el diagrama:
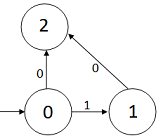
Observaciones:
El estado 0 es el inicial.
-
Accedemos al estado 2 desde q = 0 mediante un
arco etiquetado con 0, o bien, pasando por el
estado q = 1 con la secuencia de arcos
1···> 0.
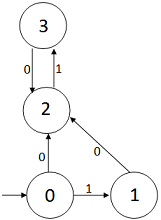
Queremos concatenar las palabras
(10)*. Para ello, debemos partir del
estado q = 2.
El operador * consiste en un bucle
entre los estados q = 2 y q = 3.
El diagrama es:
Finalmente, vamos a añadir todas las partes que nos quedan:
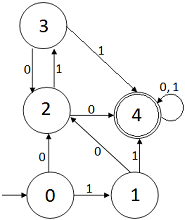
Observaciones:
El estado 0 es el inicial.
-
Accedemos al estado q = 2 desde q = 0
mediante un arco etiquetado con 0, o bien, pasando por el
estado q = 1 con la secuencia de arcos
1 ···> 0.
-
Después del bucle (10)* tenemos
(11+0). Una vez terminado el bucle
(estamos en q = 2 ) pasamos al estado q = 4.
Este cambio de estado puede ser a través del estado
q = 3 (en caso de concatenar 11) o
directamente desde q = 2 (en caso de concatenar
0).
Notemos que todo lo que hemos explicado anteriormente
es una de las dos partes de la unión del
paréntesis (el grande).
Así que también debemos llegar hasta el estado
q = 4 simplemente con la cadena 11
desde el estado inicial. Esto lo hacemos aprovechando el
estado q = 1.
El estado q = 4 es final ya que la
última parte de la expresión regular tiene un *.
Además, este estado tiene un arco con etiqueta doble para generar
las posibles secuencias finales (0+1)*.
El autómata que hemos obtenido es finito y determinista,
con 5 estados y con un sólo estado final.
PROBLEMA 6
Dado el alfabeto Σ = { a, b, c }, construir un
autómata a pila que reconozca el siguiente lenguaje:
$$ L = \{ a^i b^j c^k a^i\ | \ i,j>0;\ k=j \}$$
Ver solución
Podemos escribir las palabras como
$$ a^i b^j c^j a^i $$
De este modo, el esquema a seguir es sencillo:
se guardan en la pila todos los símbolos hasta llegar
al primer símbolo c, que no se guarda.
Cada vez que se recibe una c, se borra una
b de la pila.
La última b se borra al recibir la c.
Ahora en la pila sólo quedan a's.
Cada vez que se recibe una a, se borra otra
de la pila.
El autómata es el siguiente:
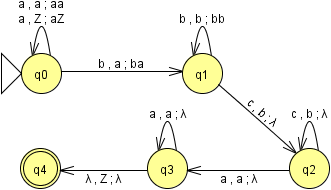
Observaciones:
El autómata acepta las palabras por estado
final (q = 4 ), aunque
también por pila vacía (al borrar el indicador de
pila vacía, Z).
El símbolo de pila Z indica pila vacía.
El autómata a pila es determinista.
PROBLEMA 7
Dado el alfabeto Σ = { a, b }, construir un
autómata a pila que reconozca el lenguaje:
$$ L = \{ w \ | w\in \{a,b \}^*, n_a (w) \geq n_b(w) \}$$
siendo
$$n_a (w)$$
el número de a's en w y n b (w)
el número de b's.
Ver solución
El autómata es el siguiente:
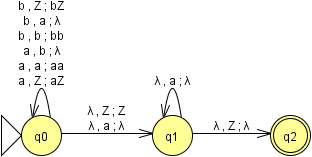
Inicio

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.




















