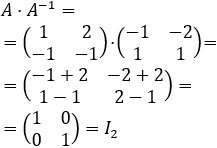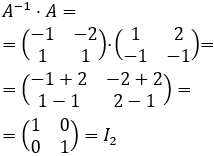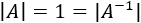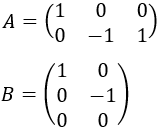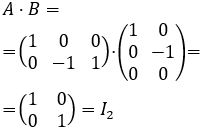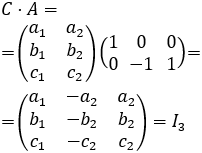Calculadora de matriz adjunta y matriz inversa (dimensión 2x2 y 3x3)

En esta página proporcionamos dos calculadoras online para obtener la matriz adjunta y la matriz inversa de matrices de dimensión 2 x 2 y 3 x 3.

Contenido de esta página:

• Introducción (definición y existencia de la inversa)
• Propiedades importantes de la inversa
• Inversa de matrices rectangulares
• Entradas que admiten las calculadoras
• CALCULADORA: inversa de una matriz 2 x 2
• CALCULADORA: inversa de una matriz 3 x 3

• Índice de calculadoras

Sea \(A\) una matriz cuadrada de dimensión \(n\) (es decir, \(n \times n\)), entonces se dice que es regular o inversible si su determinante es distinto de 0.

Ejemplo de una matriz real \(A\) de dimensión 2 y su inversa \(A^{-1}\):

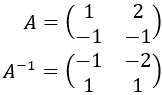
Existen varios procedimientos para calcular la matriz inversa, nosotros utilizamos la siguiente fórmula:

donde \((Adj(A))^T\) es la matriz traspuesta de la matriz de adjuntos de \(A\) y \(|A|\) es el determinante de \(A\).

Ejemplos del cálculo de la matriz inversa por el método mencionado.

Otra método básico, pero engorroso, de obtener la inversa es resolver el sistema de ecuaciones obtenido al multiplicar la matriz por una matriz formada por incógnitas (véase el ejemplo de "Inversa de matrices rectangulares"). Entre los métodos más avanzados, podemos destacar la factorización LU (factorización de la matriz como producto de matrices triangulares inferior (L) y superior (U)).

Para matrices cuadradas (dimensión \(n \times n\)), debemos conocer las siguientes propiedades de la matriz inversa:

• La inversa de la inversa de A es A: $$ (A^{-1})^{-1} = A $$
• Inversa del producto de matrices: $$ (A\cdot B)^{-1} = B^{-1}\cdot A^{-1} $$
• La inversa de la matriz traspuesta: $$ (A^{T})^{-1} = (A^{-1})^{T} $$
• Toda matriz inversa es regular: $$ |A^{-1}| \neq 0$$
• Una matriz es regular si y solo si tiene matriz inversa: $$ |A| \neq 0 \iff \exists A^{-1}$$
• El determinante de la inversa es el inverso del determinante: $$ |A^{-1}| = |A|^{-1}$$
• La solución del sistema de ecuaciones lineales compatible determinado \(A\cdot X = b\) es \( X = A^{-1}\cdot b\).

Recordad que las matrices rectangulares son las que tienen distinto número de filas y columnas (dimensión \(m \times n\)). Por tanto, no puede haber una matriz que sea al mismo tiempo la inversa multiplicativa por ambos lados (si podemos calcular el producto \(A\cdot B\), no podremos calcular el producto \(B\cdot A\)). No obstante, sí puede haber dos matrices distintas (de dimensiones distintas) que sean cada una de ellas la inversa por un lado, o bien, lo que es más común, que exista la inversa por un lado pero no por el otro.

Las entradas que admiten las calculadoras son:

• Números enteros, como 2.
• Números decimales (exactos) utilizando un punto ".", como 2.345.
• Fracciones escritas con la barra "/", como 23/15.
• No se admiten signos de operaciones o raíces y tampoco se admiten parámetros, constantes o variables.

Nota: en caso de utilizar decimales, las calculadoras aproximan con 4 decimales.

 

Si la matriz \(A\) es de dimensión 2 x 2, tiene la forma

$$ A =\left( \begin{matrix} a & b \\ c & d \\ \end{matrix}\right)$$

El determinante de \(A\) es \( det(A) = a·d - b·c\) y la traspuesta de su adjunta es

$$ (Adj(A))^T =\left( \begin{matrix} d & -b \\ -c & a \\ \end{matrix}\right)$$

Por tanto, para calcular la inversa de \(A\), sólo tenemos que dividir la matriz anterior entre el determinante de \(A\).

Calculadora:

\(A = \)

Calcular

Si la matriz \(A\) es de dimensión 3 x 3, la obtención de la matriz adjunta requiere el cálculo del determinante de 9 matrices 2 x 2. No escribimos el procedimiento, pero podéis ver ejemplos en cálculo de la matriz inversa mediante adjunción.

Calculadora:

\(A = \)

Calcular

---