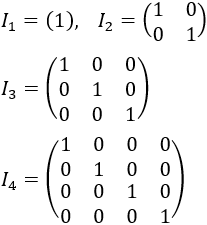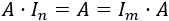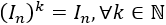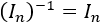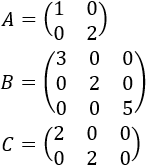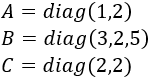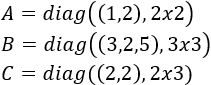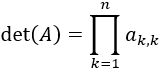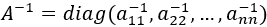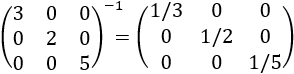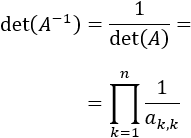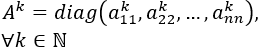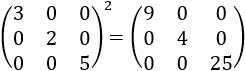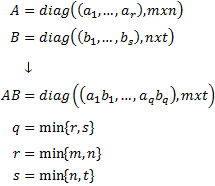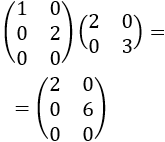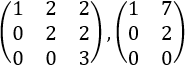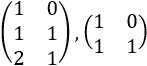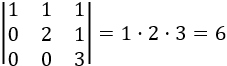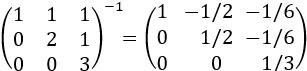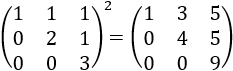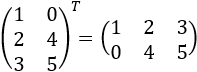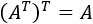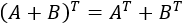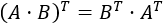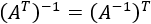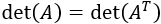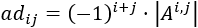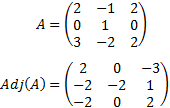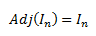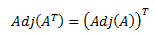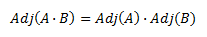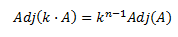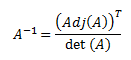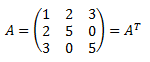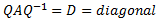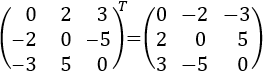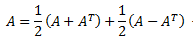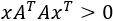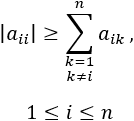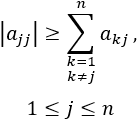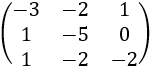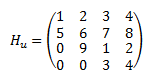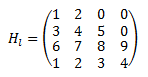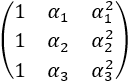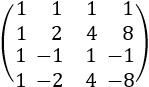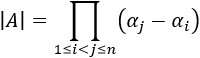3. Matriz diagonal
Una matriz \(A = (a_{ij})\) es diagonal cuando los elementos que no están en la diagonal son 0. Es decir, \(a_{ij}=0\) si \(i\neq j\).
Por ejemplo,
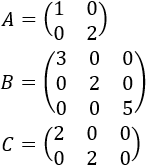
La matriz identidad es una matriz diagonal.
Normalmente, las matrices diagonales se escriben indicando su diagonal. Por ejemplo, las matrices anteriores son
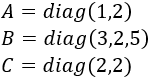
Podemos indicar la dimensión si puede dar lugar a confusión:
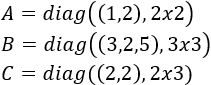
Ver propiedades
Son un caso particular de las matrices triangulares.
La matriz traspuesta de una matriz diagonal de dimensión m x n
es la matriz diagonal de dimensión n x m con la misma diagonal.
En las matrices cuadradas, el determinante
es el producto de los elementos de la diagonal:
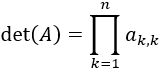
Por tanto, son regulares si, y sólo si, todos los elementos de la
diagonal son distintos de 0. En tal caso,
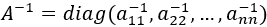
Por ejemplo,
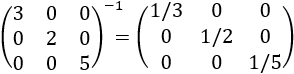
El determinante de la inversa es
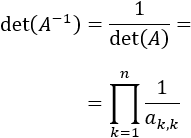
-
Potencias (para las cuadradas):
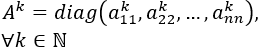
Por ejemplo,
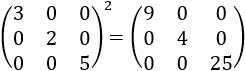
Producto de matrices diagonales: Sean las matrices \(A\) y \(B\) diagonales de dimensiones respectivas \(mxn\) y \(nxt\), entonces su producto es
una matriz diagonal de dimensión \(mxt\)
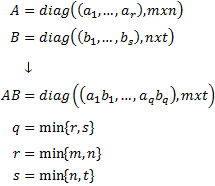
Por ejemplo,
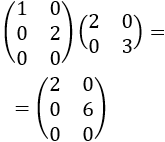
Los autovalores (valores propios) de las matrices diagonales
cuadradas son los elementos de la diagonal.
Sea la matriz \(A = (a_{i,j})\). Llamamos diagonal principal o diagonal 0 al vector formado por los elementos \(a_{i,i}\).
Análogamente, llamamos diagonal \(k> 0\) al vector formado por los elementos \(a_{i,i+k}\). Y diagonal \(-k\) al formado por los elementos \(a_{i,i-k}\).
Matriz bidiagonal:
-
Una matriz \(A\) es bidiagonal superior si sus todos los elementos por encima de la diagonal 1 y por debajo de la diagonal 0 son 0's.
Por ejemplo,

-
Una matriz \(A\) es bidiagonal inferior si sus todos los elementos por encima de la diagonal 0 y por debajo de la diagonal -1 son 0's.
Por ejemplo,

Matriz tridiagonal:
Una matriz \(A\) es tridiagonal si sus todos los elementos por encima de la diagonal 1 y por debajo de la diagonal -1 son 0's.
Por ejemplo,

Las matrices diagonales, bidiagonales y tridiagonales son casos particulares de las matrices banda.
4. Matriz triangular
Sea \(A\) una matriz de dimensión \(mxn\),
-
Es una matriz triangular superior si tiene 0's por debajo de la diagonal, es decir, si \(a_{ij} = 0\) para \(i> j\).
Por ejemplo,
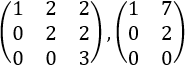
-
Es una matriz triangular inferior si tiene 0's por encima de la diagonal, es decir, si \(a_{ij} = 0\) para \(i< j\).
Por ejemplo,
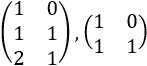
Ver propiedades
La matriz traspuesta de una triangular superior es triangular inferior y viceversa.
-
Si la matriz es cuadrada, su determinante es el producto de los elementos de la diagonal. Por tanto, es regular si, y sólo si, los elementos de la diagonal son
distintos de 0.
Por ejemplo,
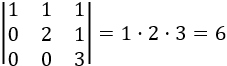
La inversa de una matriz triangular superior (inferior) es una matriz triangular superior (inferior).
Por ejemplo,
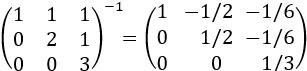
El producto de matrices triangulares superiores (inferiores) es
una matriz triangular superior (inferior).
Por ejemplo,
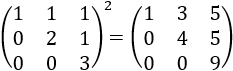
Los autovalores (valores propios) de una matriz cuadrada triangular
son los elementos de la diagonal.
5. Matriz traspuesta
La matriz traspuesta de una matriz \(A\) de dimensión \(mxn\) es una
matriz de dimensión \(nxm\) que tiene por columnas a las filas de \(A\). Se denota
como \(A^T\) (o \(A'\) si la matriz es real).
Por ejemplo,
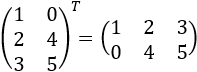
Ver propiedades
-
Traspuesta de la traspuesta:
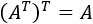
-
Traspuesta de la suma:
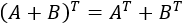
-
Traspuesta del producto:
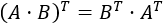
-
Inversa de la traspuesta:
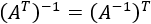
-
El determinante de una matriz regular es igual al de su traspuesta:
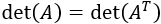
6. Matriz adjunta
Sea \(A\) una matriz de dimensión \(mxn\). Su matriz adjunta es la matriz de dimensión \(mxn\) definida por \(Adj(A) = (ad_{ij})\) siendo
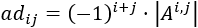
donde \(A^{i,j}\) es la matriz resultante al eliminar la fila \(i\) y columna \(j\) de \(A\).
Al elemento \(ad_{ij}\) se le llama
\((i,j)-\)cofactor (o adjunto) de la matriz
\(A\).
Por ejemplo,
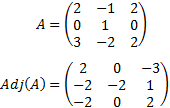
Ver propiedades
-
Adjunta de la identidad:
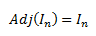
-
Adjunta de la traspuesta:
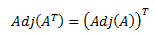
-
Adjunta del producto:
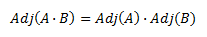
-
Si \(A\) es de dimensión \(n\) y \(k\) un escalar:
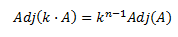
-
Si \(A\) es regular, su inversa es:
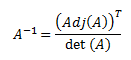
Esta propiedad se usa con frecuencia para el cálculo de la inversa:
matriz inversa mediante adjunción.
7. Matriz simétrica
Una matriz \(A\) es simétrica si es igual a su traspuesta, es decir, \(A = A^T\). Como consecuencia de la definición, la matriz \(A\) tiene que ser cuadrada.
Por ejemplo,
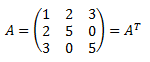
Ver propiedades
-
La inversa de una matriz simétrica regular es simétrica.
-
La adjunta de una simétrica es simétrica.
-
La suma de simétricas es simétrica. El producto lo es si, y sólo si,
también es conmutativo.
-
Si \(A\) es una matriz cuadrada, entonces \(A+A^T\) es simétrica.
-
Los autovalores (valores propios) de una matriz
cuadrada, real y simétrica son reales.
-
Autovectores (vectores propios) de autovalores
distintos de una matriz cuadrada y real son ortogonales.
-
Una matriz cuadrada y real, A, es simétrica
si, y sólo si, es
diagonalizable mediante una matriz de paso ortogonal, Q.
Es decir,
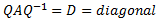
8. Matriz antisimétrica
Una matriz \(A\) es antisimétrica si es la matriz opuesta de su traspuesta, es decir, \(A = -A^T\). Como consecuencia de la definición, la matriz \(A\) tiene que ser cuadrada.
Por ejemplo,
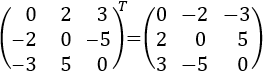
Ver propiedades
-
Si \(A\) es una matriz cuadrada, entonces \(A-A^T\) es antisimétrica.
-
Toda matriz cuadrada \(A\) puede escribirse como la suma de una matriz simétrica y una matriz antisimétrica:
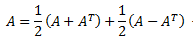
9. Matriz definida positiva
Una matriz \(A\) de dimensión \(mxn\) es definida positiva si para todo vector \(x = ( x_1 ,..., x_n )\) se cumple
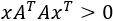
Si se cumple con la desigualdad \(\geq \), diremos que la matriz es semi definida positiva.
Ver propiedades
10. Matriz diagonalmente dominante
Una matriz \(A = (a_{ij})\) cuadrada de dimensión \(n\) es diagonalmente dominante por filas (RDD) si
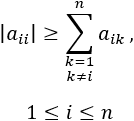
Por ejemplo,

Una matriz \(A = (a_{ij})\) cuadrada de dimensión \(n\) es diagonalmente dominante por columnas (CDD) si
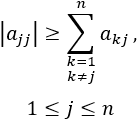
Por ejemplo,
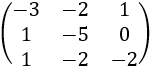
Si se cumple con el signo estricto, diremos estrictamente diagonalmente dominante por filas o columnas. Los ejemplos son estrictamente.
Ver propiedades
11. Matriz Hessenberg
Una matriz cuadrada \(A\) de dimensión \(n> 1\) es Hessenberg superior si todos los elementos bajo la diagonal -1 son nulos.
Por ejemplo,
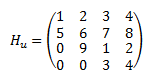
Una matriz cuadrada \(A\) de dimensión \(n> 1\) es Hessenberg inferior si todos los elementos sobre la diagonal 1 son nulos.
Por ejemplo,
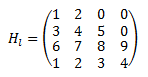
Ver propiedades
12. Matriz Vandermonde
Una matriz cuadrada \(A = (a_{ij})\) es de Vandermonde si \(a_{ij} = \alpha_i ^{j-1}\).
Si es de dimensión 3, tiene la forma
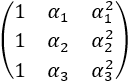
Ejemplo de una matriz Vandermonde de dimensión 4:
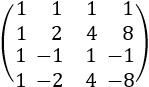
Ver propiedades


Matrices especiales -
© matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.