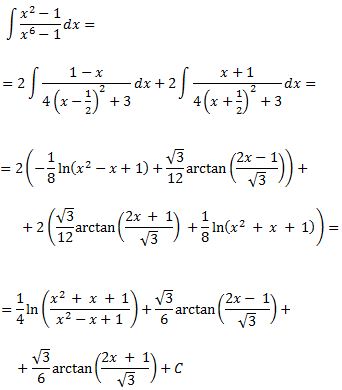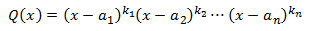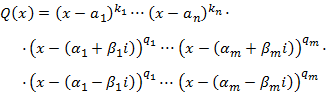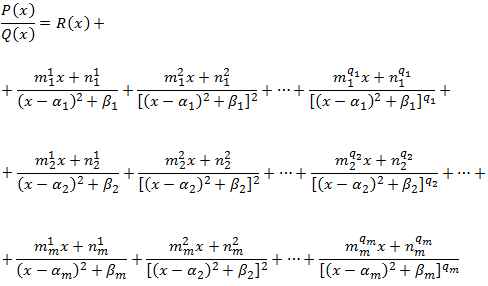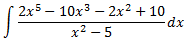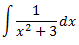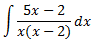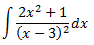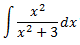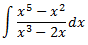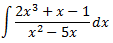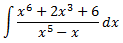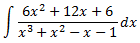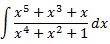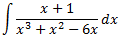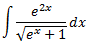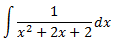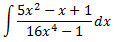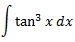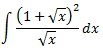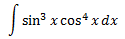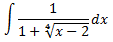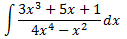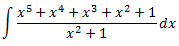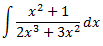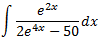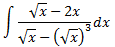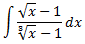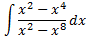Sigui la integral
$$\int{\frac{P(x)}{Q(x)}}dx$$
on \(P(x)\) i \(Q(x)\) són els polinomis del numerador i del denominador,
respectivament.
Distingim els següents casos:
-
grau( P ) \(\geq\) grau( Q ): efectuem la divisió dels polinomis.
-
grau( P ) < grau( Q ):
En aquest cas, aplicarem el Teorema Fonamental de l'Àlgebra. Subcasos:
Cas 1: grau de P major o igual que el de Q
En aquest cas, el mètode consisteix en efectuar una divisió polinòmica per poder descompondre la integral. Abans d'açò, però, s'han de factoritzar els polinomis del numerador i del denominador (expressar-los com a productes de factors de la forma (x - arrel) ) per tal simplificar l'integrand.
Per tant, donada la integral
$$\int{\frac{P(x)}{Q(x)}}dx$$
Al efectuar la divisió, tindrem que
$$P(x) = Q(x) \cdot C(x) + R(x)$$
sent C(x) el polinomi quocient i R(x) el polinomi residu de la divisió.
Si dividim la igualtat anterior entre Q(x) obtenim
$$\frac{P(x)}{Q(x)} = C(x) + \frac{R(x)}{Q(x)}$$
D'aquesta manera, aplicant les propietats de les integrals, haurem descompost la integral en la suma de dues integrals:
$$\int{\frac{P(x)}{Q(x)}}dx =\int{C(x)}dx + \int{\frac{R(x)}{Q(x)}}dx$$
Cas 2: grau de P menor que el de Q
Cas (a): totes les arrels de Q són reals
Podem factoritzar el polinomi \(Q\) i escriure'l com
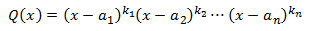
on cada \(a_i\) són les arrels (reals) de \(Q\) i \(k_i\) és el grau de multiplicitat
de l'arrel \(a_i\), és a dir, el nombre de vegades que es repiteix l'arrel.
Nota: per comoditat, estem suposant que els polinomis són mònics, és a dir, que 1 és el seu coeficient director.
Si cal, per buscar les arrels dels polinomis, podem aplicar la regla de Ruffini.
Segons el Teorema Fonamental de l'Àlgebra, podem expressar el quocient \(P(x)/Q(x)\) com una suma de quocients als que denominem
fraccions simples:

on els termes \(b_i^j\) són reals i els desconeixem.
Haurem de cercar-los donant valors a x.
Cas (b): NO totes les arrels de Q són reals
Factoritzem el denominador, \(Q\), obtenint una expressió com la següent
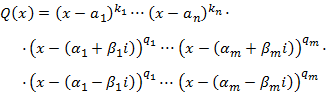
on \(a_i\) són les arrels reals de \(Q\) amb multiplicitats \(k_i\) i
\(\alpha_j + i\beta_j\) són les arrels complexes amb multiplicitats \(q_j\).
Nota: si un complex
\(z=\alpha + i\beta\) és arrel d'un polinomi, aleshores el seu conjugat \(\overline{z}=\alpha_j - i\beta_j\) també ho és i, a més, tenen la mateixa multiplicitat.
Pel Teorema Fonamental de l'Àlgebra,
podem escriure el quocient \(P(x)/Q(x)\) com
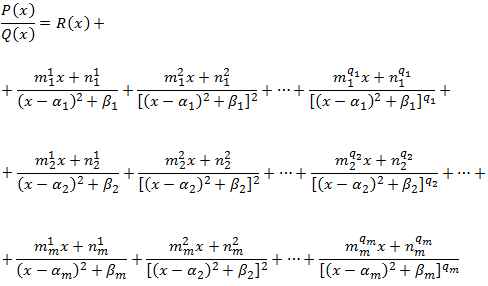
on \(m_i^j\) i
\(n_i^j\) són constants reals que desconeixem.
Nota: no s'ha confondre el sunbíndex \(m\) (nombre d'arrels complexes del polinomi) amb les constants \(m_i^j\).
El polinomi \(R(x)\) és la suma de fraccions simples associada a les arrels reals que ja sabem com escriure (cas anterior) i que hem omitit per tal de simplificar la notació.
Observeu que es tracta del mateix procediment encara que les fraccions simples associades a les arrels complexes tenen una forma distinta.
Hem de calcular les constants \(m_i^j\) i \(n_i^j\). Per calcular-les, multipliquem la igualtat d'abans per la factorització de \(Q\) i donem valors
a \(x\) per obtenir un sistema d'equacions lineals. Una vegada calculades, podrem expressar la integral com una suma d'integrals simples.
Integral 1
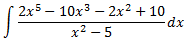
Veure solució
Al ser el grau del polinomi del numerador major que el del denominador, dividim els polinomis:
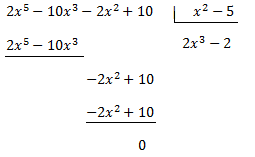
Per tant, podem escriure el dividend com el producte del divisor i del quocient (més el residu, que és 0):
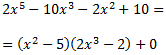
Dividint entre el polinomi quocient, podem escriure la fracció de polinomis com un polinomi de grau 3:
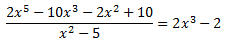
D'aquesta manera, la integral és
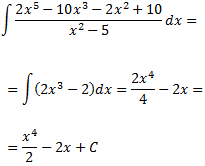
Integral 2
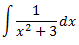
Veure solució
Al ser el grau del polinomi del denominador major que el del numerador, no podem dividir els polinomis.
En principi, hauríem d'aplicar el Teorema Fonamental de l'Àlgebra però, per la forma de l'integrand, podem transformar-lo en la derivada d'un arctan. Operem un poc:
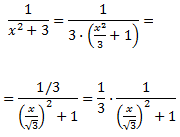
Per tant, la integral que queda és immediata:
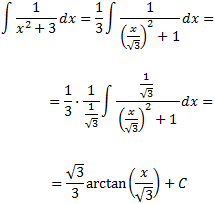
Integral 3
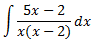
Veure solució
Al ser el grau del polinomi del denominador major que el del numerador, apliquem el Teorema Fonamental de l'Àlgebra per expressar el quocient com una suma de fraccions simples:
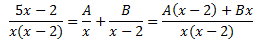
Per obtenir les constants A i B, donem valors a x en la igualtat anterior. És suficient
comprovar que els numeradors siguin iguals ja que els denominadores ho són:
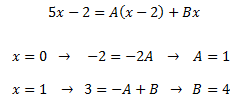
Llavors, podem escriure la integral com una suma i, aplicant les seves propietats, com una suma d'integrals:
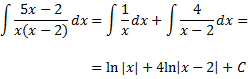
Nota: l'argument d'un logaritme ha de ser un valor absolut, excepte que aquest sigui sempre positiu (per exemple, si és \(x^2\)).
Integral 4
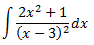
Veure solució
Desenvolupem el denominador:
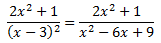
Com que els graus dels polinomis són el mateix, dividim els polinomis:
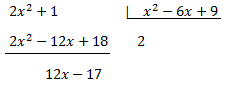
Escrivim el dividend com el producte del divisor pel quocient més el residu:
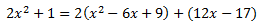
Al dividir en ambdós costats pel divisor s'obté una suma:
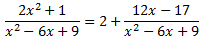
Escrivim la integral com la suma de la integral d'una constant i la integral d'un quocient de polinomis:
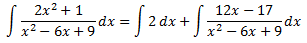
La primera de les integrals és immediata. La segona és un quocient de polinomis. Com que el grau del denominador és major, cerquem les seves arrels per aplicar el Teorema Fonamental de l'Àlgebra i expressar el quocient com una suma de fraccions simples. Ja sabem que
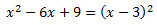
És a dir, tenim una arrel real doble i ninguna arrel complexa. Llavors, la
descomposició en fraccions simples és de la forma
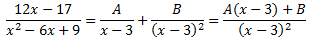
Per obtenir les constants, donem valors a x en la següent igualtat:
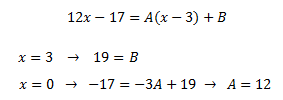
Aquesta descomposició ens permet descompondre la integral en una suma d'integrals:

Ambdues integrals són immediates:
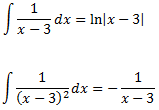
Per tant, el resultat de la integral inicial és
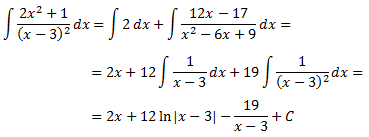
Integral 5
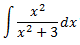
Veure solució
Com que el grau dels polinomis del numerador i del denominador són iguals, dividim els polinomis:
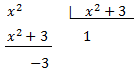
Per tant, podem escriure el numerador com
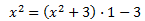
D'on obtenim la descomposició del quocient en una suma:
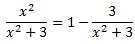
Escrivim la integral com una suma d'integrals:
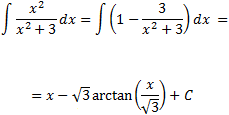
La segona integral l'hem resolt en l'exercici 2.
Integral 6
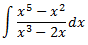
Veure solució
Nota: podem simplificar l'integrand:
$$\frac{^5-x^2}{x^3-2x} = \frac{x^4-x}{x^2-2}$$
Encara que nosaltres no ho hem fet a la resolució de la integral perquè en aquest procediment no canvia massa.
Al ser el grau del polinomi del numerador major que el del denominador, dividim els polinomis:
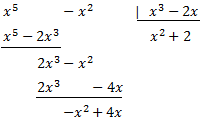
Açò ens permet escriure el quocient com una suma de fraccions més simples:
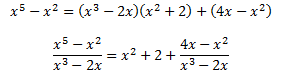
Així, podem descompondre la integral com una suma d'integrals:
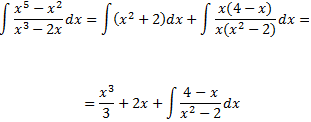
El grau del polinomi del denominador de la integral que queda és major que el del numerador. Cerquem les arrels del denominador:
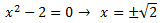
Com que les arrels són reals, pel Teorema Fonamental de l'Àlgebra, podem escriure el quocient com una suma de dues fraccions simples:
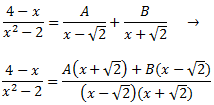
Donem valors a x en la igualtat per determinar les constants A i B:
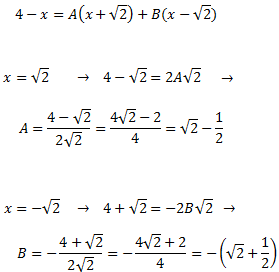
Per tant, la descomposició del quocient és
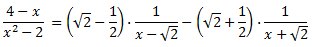
Llavors, el resultat de la integral inicial és
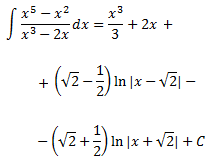
Integral 7
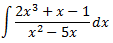
Veure solució
Com que el grau del polinomi del numerador és major que el del denominador, dividim els polinomis:
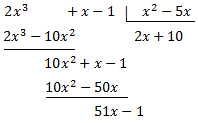
El numerador es pot escriure com
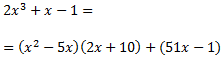
Dividint entre el divisor la igualtat anterior, el quocient dels polinomis es pot escriure com la següent suma:
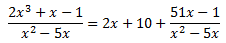
D'aquesta manera, podem expressar la integral com la suma
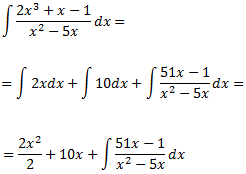
En la integral que queda, el grau del polinomi del denominador és major que el del numerador. Cerquem les arrels del denominador per descompondre la fracció en fraccions simples:
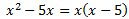
Al ser reals les arrels (0 i 5), pel Teorema Fonamental de l'Àlgebra, el quocient es pot escriure com la suma
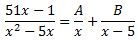
Per calcular els valors de les constants A i B, donem valors a x en la igualtat:
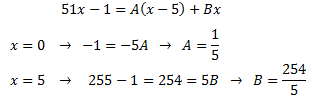
Per tant, la integral es pot escriure com
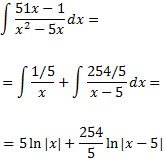
Llavors, el resultat de la integral inicial és
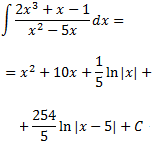
Integral 8 (dificultat alta)
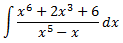
Veure solució
Dividim els polinomis:
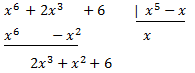
D'on es dedueix la següent descomposició del dividend:
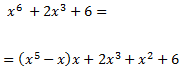
Ecrivim la integral com una suma:
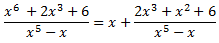
Açò ens permet escriure la integral com la suma de dues integrals:
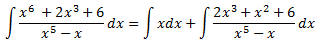
La primera integral és immediata. Calculem la segona:
Al ser el grau del denominador major que el del numerador, cerquem les arrels del denominador per aplicar el Teorema Fonamental de l'Àlgebra:
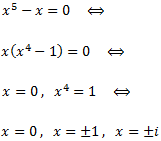
Tenim 3 arrels reals i dues arrels complexes.
Descomponem la fracció en fraccions simples:
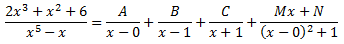
És a dir,
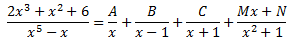
Operant, s'obté la igualtat
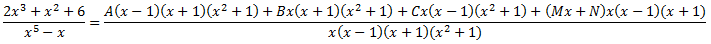
Calculem les cinc constants A, B, C, M i N donant valors a x en la igualtat:
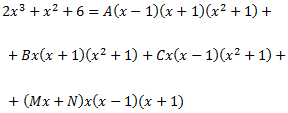
Utilitzarem \(x=1\), \(x=-1\), \(x=0\), \(x=2\) i \(x=-2\):
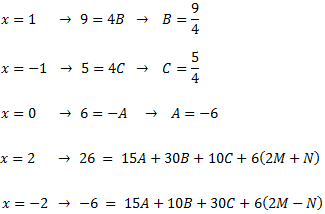
Per calcular les constants \(M\) i \(N\), hem de resoldre un sistema d'equacions lineals la solució del qual és \(M=5/2\) i \(N=1\).
Les constants són
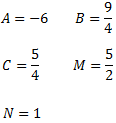
La descomposició que queda és
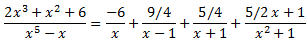
D'aquesta manera, la integral es descompon en la suma de altres quatre integrals més senzilles:
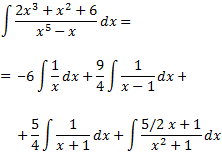
Les tres primeres integrals són immediates. Calculem la quarta:
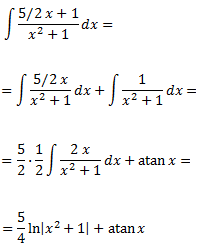
El resultat de la integral inicial és
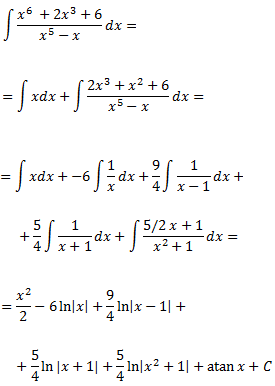
Integral 9
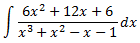
Veure solució
El grau del polinomi del denominador és major que el del numerador. Apliquem la regla de Ruffini
per calcular les arrels del denominador.
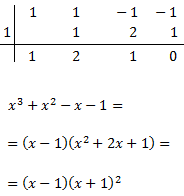
Ara factoritzem el numerador per intentar simplificar la fracció:
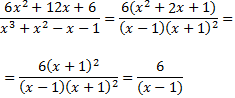
Per tant, la integral que queda és immediata:
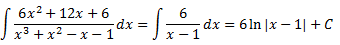
Integral 10
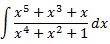
Veure solució
En realitat, es tracta d'una integral immediata ja que si factoritzem els polinomis podem simplificar l'integrand
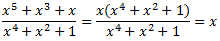
Per tant, el resultat de la integral és
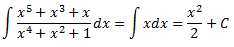
Integral 11
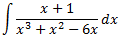
Veure solució
Descomponem la fracció de l'integrand en una suma.
Per fer-ho, cerquem les arrels del denominador:
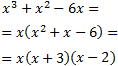
Totes les arrels són reals i simples. Pel Teorema Fonamental de l'Àlgebra, podem escriure el quocient com
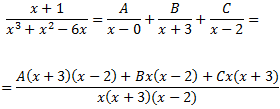
Donem valors a x en la següent igualtat per determinar les constants:
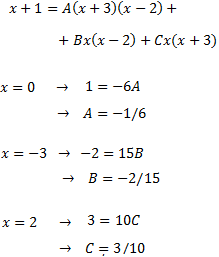
Per tant, la descomposició de la fracció és

Finalment, tenim
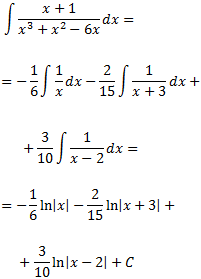
Integral 12
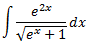
Veure solució
Al aplicar el canvi de variable
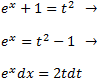
La integral queda com
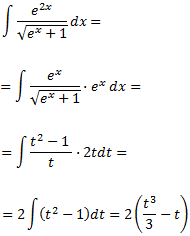
Com que ja hem resolt la integral, només cal desfer el canvi de variable. Primer aïllem
t:
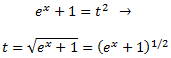
Obtenim
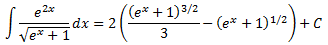
Integral 13
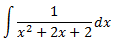
Veure solució
El grau del polinomi del numerador és major que el del denominador. Calculem les arrels del polinomi del denominador:
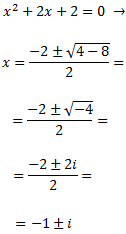
Pel Teorema Fonamental de l'Àlgebra, podem expressar el quocient com
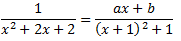
Donem valors a x per calcular les constants a i b:
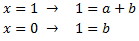
La solució del sistema anterior és
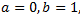
Llavors,
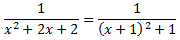
Nota: el resultat obtingut és evident i pot obtenir-se
directament sense necessitat d'aplicar el teorema. Però, ho fem fet així per seguir l'algoritme de resolució.
La integral és immediata per ser la derivada d'un arctan:
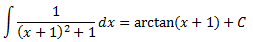
Integral 14
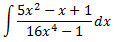
Veure solució
El grau del polinomi del denominador és major que el del denominador.
Cerquem les arrels del denominador:
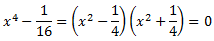
Les arrels són
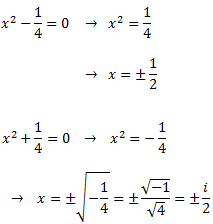
Tenim arrels reals i complexes. Pel Teorema Fonamental de l'Àlgebra, podem escriure el quocient com
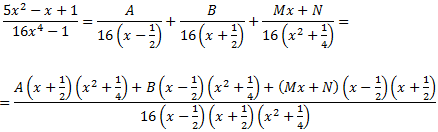
Nota: al no ser el denominador un polinomi mònic (coeficient director 1), escrivim en el denominador de les fraccions simples el seu coeficient director.
Per obtenir les constants, donem valors a x en la igualtat:
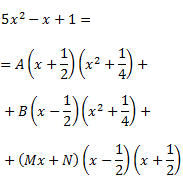
Per facilitar els càlculs, comencem donant els valors que són arrels (axí obtenim zeros):
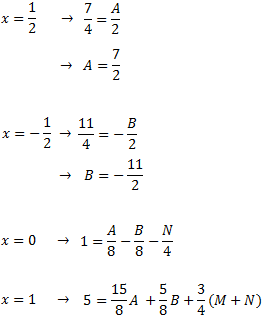
Resolem el sistema d'equacions obtenint les quatre constants:
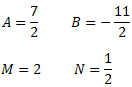
Per tant, la descomposició de la fracció és
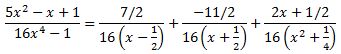
Descomponem la integral inicial:
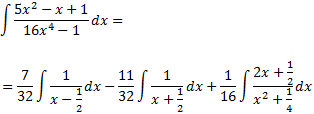
Les dues primeres integrals són immediates:
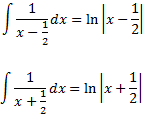
Calculem la tercera integral transformant l'integrand en la suma de les derivadas d'un arctan i d'un ln:
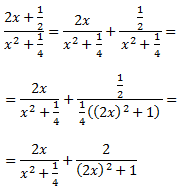
La seva integral és
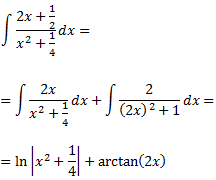
Per tant, el resultat de la integral inicial és
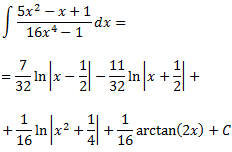
Integral 15
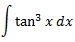
Veure solució
Hem classificat aquesta integral com a racional ja que si apliquem el canvi de variable
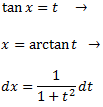
Obtenim la integral
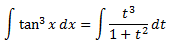
Com que el grau del polinomi del numerador és major que el del denominador, dividim els polinomis:
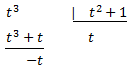
D'on s'obté
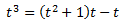
Dividim entre t:
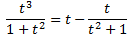
Finalment, calculem la integral i desfem el canvi de variable:
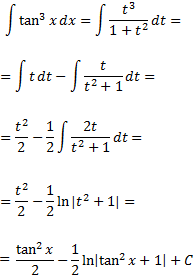
Integral 16
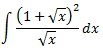
Veure solució
En realitat, aquesta integral encaixa més en la secció d'integració per substitució. No obstant això, l'integrand és una fracció.
Apliquem el canvi de variable
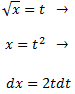
I calculem la integral resultant:
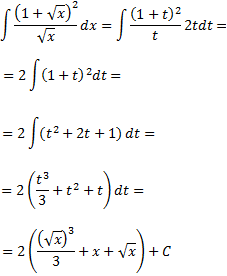
Integral 17
Veure solució
Aplicarem el canvi de variable següent:
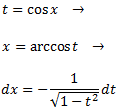
I emprarem la identitat fonamental de la trigonometria:
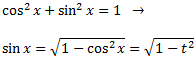
Resolem la integral:
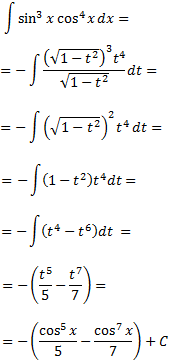
Integral 18
Veure solució
Apliquem el canvi de variable
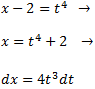
I obtenim una integral racional:
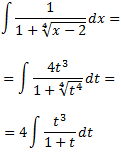
Dividim els polinomis:
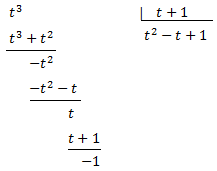
D'on obtenim
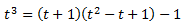
Escrivim el quocient de polinomis com una suma:
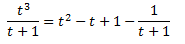
Llavors, la integral és
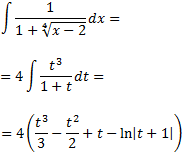
Desfem el canvi de variable:
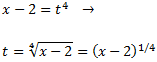
Per tant,
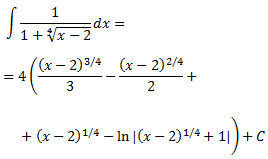
Integral 19
Veure solució
Cerquem les arrels del denominador:
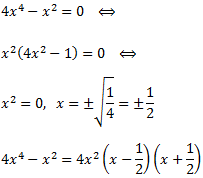
Les quatre arrels són reals. Pel Teorema Fonamental de l'Àlgebra, podem descompondre la fracció en fraccions simples.
A diferència de l'exercici 14, farem que el polinomi del denominador sigui mònic (coeficient director 1) escrivint el 4 en el numerador en forma de fracció 1/4:
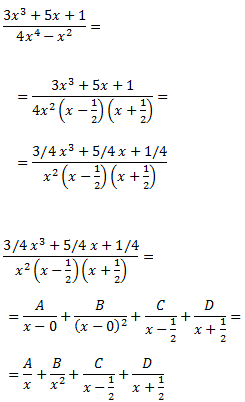
D'on s'obté la igualtat
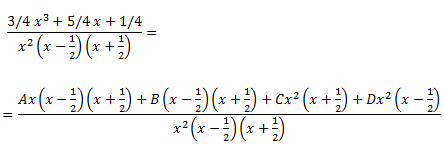
Per calcular les constants A, B, C i D, donem valors a x després d'igualar els numeradors
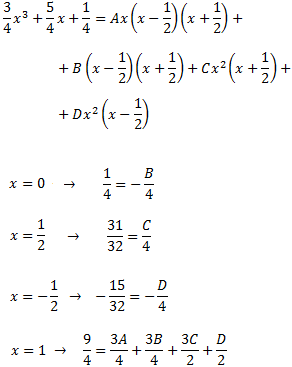
Resolem el sistema d'equacions lineals la solució del qual és
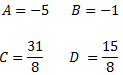
La descomposició en fraccions simples és
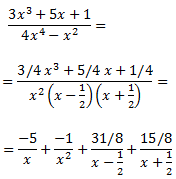
Descomponem la integral en una suma d'integrals immediates:
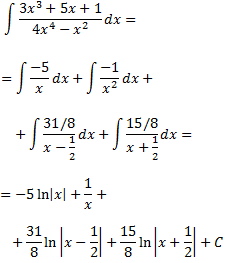
Integral 20
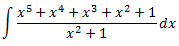
Veure solució
Dividim els polinomis:
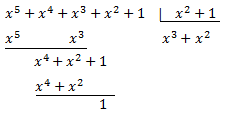
El dividend és
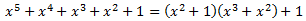
Al dividir l'expressió anterior, s'obté una descomposició de la fracció:
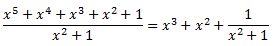
Descomponem la integral:
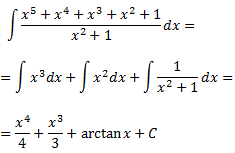
Integral 21
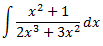
Veure solució
Cerquem les arrels del denominador:
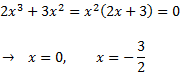
Escrivim el denominador en forma factoritzada:
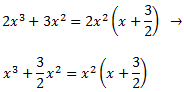
Pel Teorema Fonamental de l'Àlgebra, podem escriure el quocient com
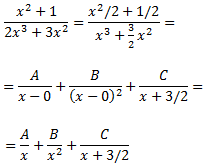
Al sumar les fraccions, s'obté
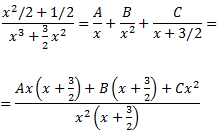
Donem valors a x en la següent igualtat per obtenir les constants A, B i C:
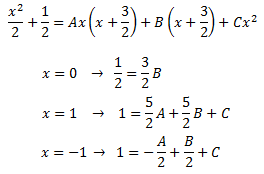
Resolem el sistema d'equacions lineals:
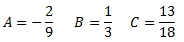
Així,
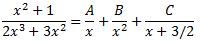
D'on
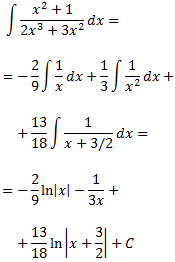
Integral 22
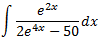
Veure solució
Apliquem el següent canvi de variable:
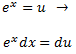
La integral resultant és
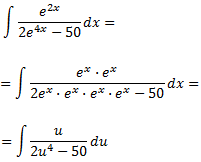
Calculem les arrels del denominador:
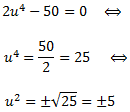
Les arrels són
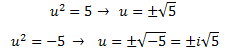
Per tant, la factorització del polinomi és
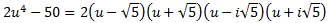
És a dir,
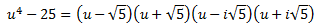
Podem escriure el quocient com
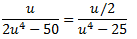
Apliquem el Teorema Fonamental de l'Àlgebra:
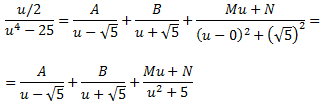
Sumem les fraccions:
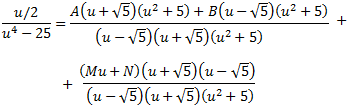
Donem valors a u en la següent igualtat per calcular les constants A, B, M i N:
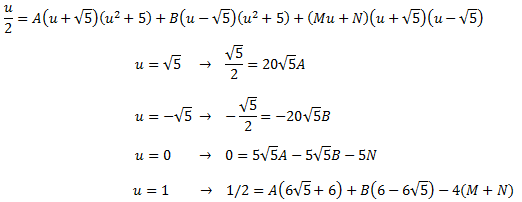
La solució el sistema d'equacions lineals és
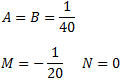
La descomposició de la fracció és
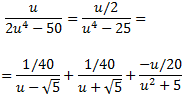
Per tant,
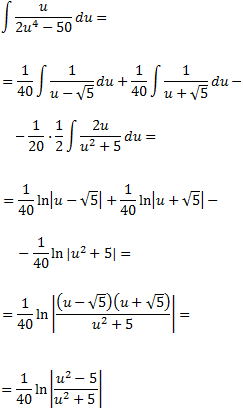
Finalment, desfem el canvi de variable:
$$ e^x = u \leftarrow x = ln(u) $$
El resultat de la integral és
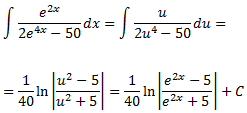
Integral 23
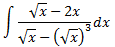
Veure solució
Apliquem el canvi de variable
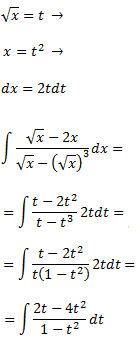
Dividim els polinomis:
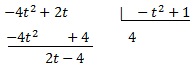
El dividend es pot escriure com
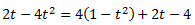
Dividint en la igualtat, obtenim
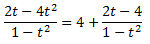
Llavors,
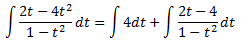
La primera integral és immediata. Calculem la segona:
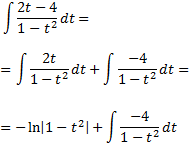
Resolem l'última integral aplicant el Teorema Fonamental de l'Àlgebra:
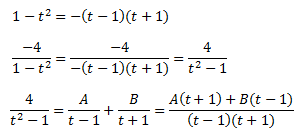
Calculem les constants:
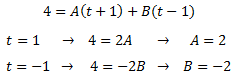
La descomposició és
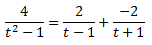
D'on
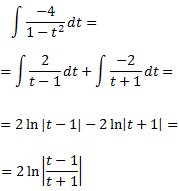
Per tant,
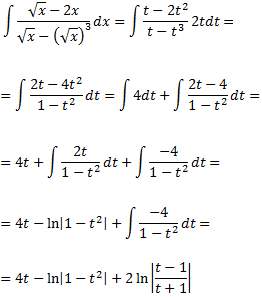
Finalment, desfem el canvi de variable:
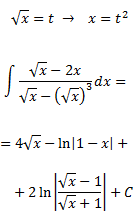
Integral 24
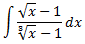
Veure solució
Aplicarem un canvi de variable però, si escollim
$$ x = y^2 $$
Aleshores,
$$ y = \sqrt{x} $$
D'aquesta manera desapareix l'arrel quadrada. Però,
$$ \sqrt[3]{x} = \sqrt[3]{y^2} $$
Alguna cosa semblant ocorre si escollim
$$ x = y^3 $$
En canvi, si escollim com exponent al m.c.m(2,3) = 6 (mínim comú múltiple), aleshores
desapareixen els dos signes radicals:
$$ x = y^6 $$
De manera que
$$ \sqrt{x} = \sqrt{y^6} = y^3 $$
$$ \sqrt[3]{x} = \sqrt[3]{y^2} = y^2$$
$$dx = 6y^5 dy $$
Apliquem el canvi en la integral:
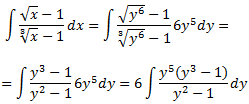
Dividim els polinomis:
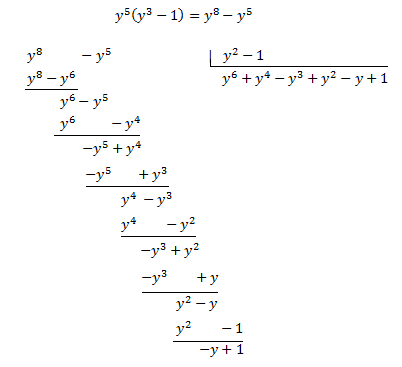
Consegüentment, el numerador es pot escriure com
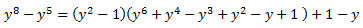
D'on s'obté la següent descomposició:
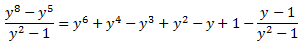
De manera que podem escriure la integral com una suma d'altres integrals més senzilles:
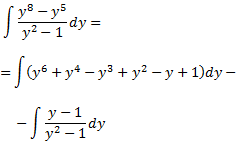
La última integral és immediata:
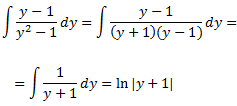
Així, el resultat de la integral és:
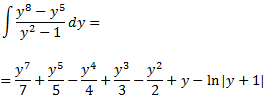
Així doncs, la integral inicial és
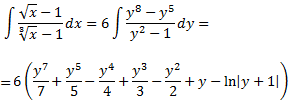
Desfem el canvi de variable:
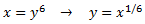
Substituint, el resultat de la integral inicial és
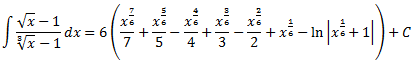
Nota: el resultat pot simplificar-se més (les fraccions de les potències no són irreductibles).
Integral 25 (dificultat alta)
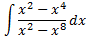
Veure solució
Cerquem les arrels del denominador però, abans, simplifiquam la fracció:
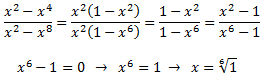
Recordem que les arrels n-èsimes d'un complexe z = a + bi són
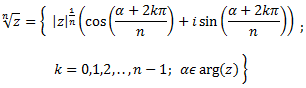
Si a≠0, en el conjunt anterior podem utilitzar
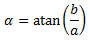
Hem de calcular les arrels 6-èsimes de z = 1:
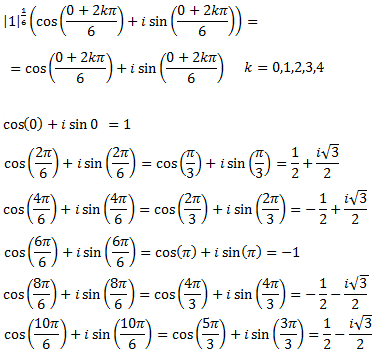
Per tant, tenim les 6 arrels
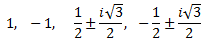
Aplicant el Teorema Fonamental de l'Àlgebra, podem escriure
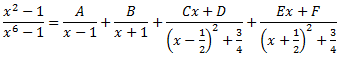
Donem valors a x en la següent igualtat per obtenir les constants:
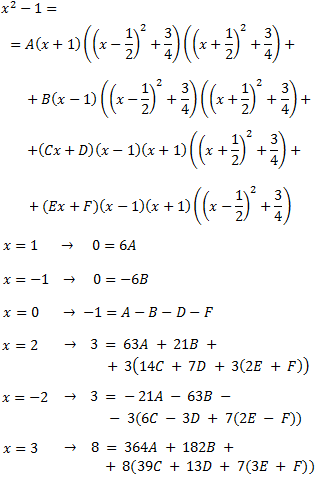
La solució del sistema d'equacions anterior és
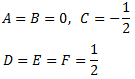
Així, la descomposició de la fracció és
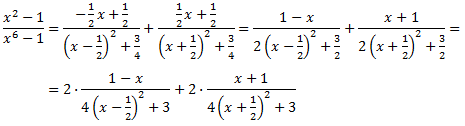
La integral inicial queda com
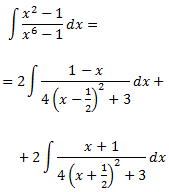
Resolem la primera integral:
Operem en l'integrand per obtenir les derivades de l'arctan i del ln:
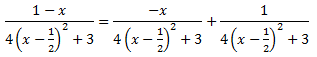
Operem en la fracció anterior de la dreta:
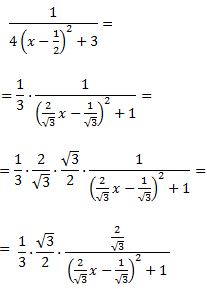
D'on
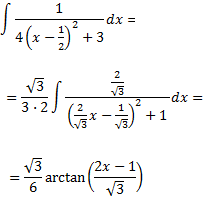
Calculem la integral de la primera fracció tenint en compte que
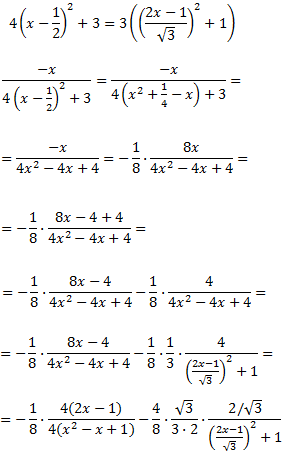
Així,
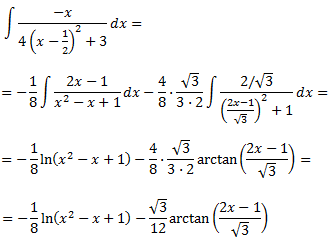
Ja tenim la primera integral. Ara calculem la segona:
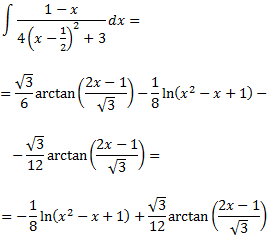
Si ens fixem, només canvia el coeficient director del polinomi del numerador. Obviem el procediment ja que s'obté de manera semblant que l'anterior:
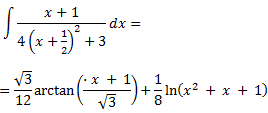
Finalment, tenim que