Matrices: diagonalización
Teorema Una matriz A real de dimensión n (cuadrada) es diagonalizable en los reales si y sólo si existe una base de |
|---|
Demostración (Notación MatLab) Supongamos que A es diagonalizable: Sea A = PDP-1 con P regular y D diagonal una diagonalización de A. Multiplicando por P tenemos que AP = DP. Consideremos D = diag(d1 ,…,dn ). La columna j de D es D(:,j): 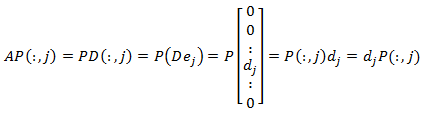
Es decir, dj es un valor propio de A y D(:,j) un vector propio asociado a dj. Por tanto, el sistema { P(:,i) }ni=1 está formado por vectores propios de A y, además, es una base por ser la matriz P regular. De donde deducimos que si una matriz es diagonalizable, la matriz diagonal a la que es semejante está formada por valores propios de A. Supongamos ahora que { xi}i=1n es una base formada por vectores propios de A. Puesto que los vectores son linealmente independientes y que los vectores propios asociados a un autovalor son un subespacio, existen n autovalores, di , tales que Axi = dixi . Como la matriz es real y la base también, los autovalores también lo son. Definimos las matrices D = diag(d1,…,dn ) y P que tiene por columnas P(:,i) = xi, de dimensión n. La matriz P es regular por ser sus columnas una base. 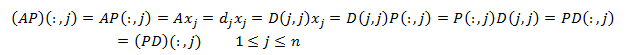
De donde AP = PD y, al ser P regular, A = APP-1 = PDP-1. |
 n formada por vectores
propios de A.
n formada por vectores
propios de A.