Matrices: diagonalización
| Teorema Toda matriz real y simétrica A es diagonalizable. Además, se tiene que A = PDP-1 donde D es diagonal y P ortogonal (P -1 = P T). |
|---|
| Demostración (Notación MatLab) Lo demostraremos por inducción sobre k, la dimensión de A. Sea k = 1: La matriz es de la forma A = [a], siendo a en Podemos escribir A = I·A·I donde I = [1] es la matriz identidad de dimensión 1, que es regular y ortogonal, y A es diagonal. Tenemos pues una diagonalización de A. Supongamos que es cierto para dimensión k-1 (hipótesis de inducción). Veamos que se cumple para dimensión k: Sea A una matriz real simétrica de dimensión k. Puesto que A es simétrica, su espectro (autovalores) es positivo y real. Sea μ un autovalor
de A. Existe x de Al ser x de norma2 1, existe una matriz Q real, de dimensión k y ortogonal cuya primera columna es el vector x ya que: podemos completar el sistema {x} hasta una base { x }U{ yi }ki=2 y aplicar el método de Gram-Schmidt comenzando por x para obtener la base ortonormalizada {x}U{xi }ki=2. Luego definimos Q(:,1) = x , Q(:,i) = xi y se tiene que es una matriz ortogonal puesto que 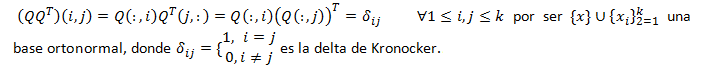
Consideremos el producto Q -1AQ = QTAQ. Su primera columna es 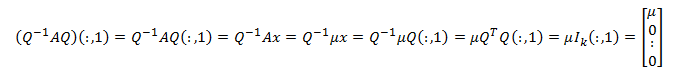
Por ser A simétrica y Q ortogonal, (Q -1AQ)T = Q -1AQ ya que (Q -1AQ)T = (QTAQ)T = QTAT(QT)T = QTAQ = Q -1AQ. En particular tenemos que 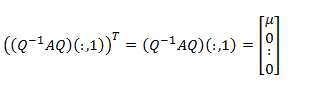
Con lo que Q -1AQ tiene la siguiente estructura por bloques 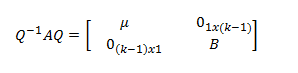
donde 0ixj representa la matriz nula de dimensión ixj y B es la matriz B = (Q -1AQ)(2:k,2:k) que es de dimensión (k-1)x(k-1) y, por tanto, diagonalizable mediante una matriz ortogonal por hipótesis de inducción. Sean, pues,
R de 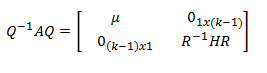
Podemos escribir la matriz como producto (por bloques) de matrices: 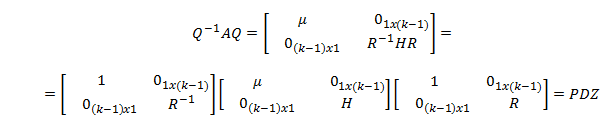
Nótese que D de 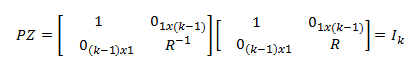
De donde se deduce que Z = P -1. Además, P = ZT por ser R ortogonal. Es decir, Z = P -1 = PT por tanto, 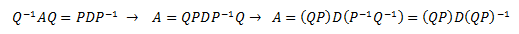
Y ahora sólo hay que tener en cuenta que el producto de ortogonales es ortogonal ya que 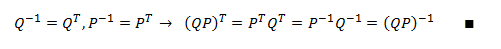
|
 .
.