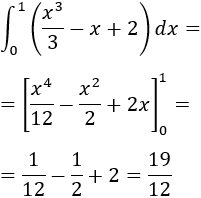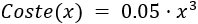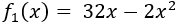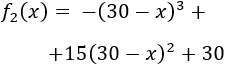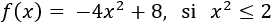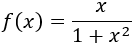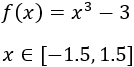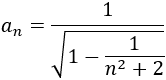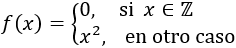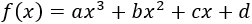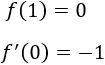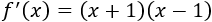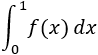Contenido de esta página:
Introducción
Los siguientes problemas resueltos son problemas de optimización mediante cálculo diferencial básico (nivel bachillerato). Para resolverlos, se precisa derivar y aplicar el criterio de la primera derivada.
Para resolver los siguientes problemas optimización de cálculo diferencial básico, utilizaremos el siguiente método:
-
Plantear la función \(f\) que debe optimizarse (maximizar o minimizar).
-
Calcular la derivada de la función \(f\).
-
Buscar los puntos críticos de \(f\) igualando a 0 la derivada \(f'\).
-
Estudiar la monotonía de la función (creciente o decreciente) en los intervalos que generan los puntos críticos para determinar el tipo de extremos (relativos o absolutos).
Solamente se utiliza el criterio de la primera derivada (excepto en el Problema 22 y en el Problema 23) puesto que no todos los alumnos estudian el de la segunda derivada.
Toda la información necesaria para seguir los pasos del método de arriba se encuentra en:
Problemas Resueltos
Problema 1
Se quiere construir una caja sin tapa a partir de una hoja de cartón de 20x10cm. Para ello, se corta un cuadrado de lado L en cada esquina y se dobla la hoja levantando los cuatro laterales de la caja.
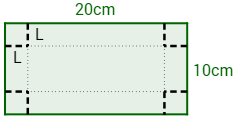
Determinar las dimensiones de la caja para que su volumen sea máximo si el lado \(L\) debe medir entre 2 y 3 cm (\(2\leq L\leq 3\)).
Solución
Si \(a\) es el ancho de la caja, \(h\) es su altura y \(p\) es su profundidad, entonces su volumen es
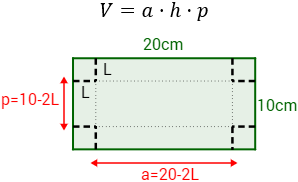
Al cortar los cuatro cuadrados de lado \(L\), el ancho de la caja es
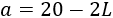
La profundidad es
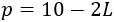
Por último, la altura coincide con el lado del cuadrado recortado:
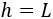
Luego el volumen de la caja en función de \(L\) es (paso 1)
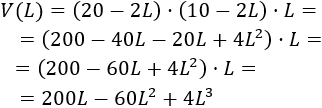
Derivamos la función volumen (paso 2):
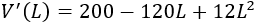
Igualamos a 0 la derivada y resolvemos la ecuación para encontrar los puntos críticos (paso 3):
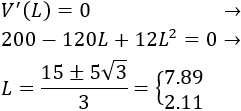
Situamos los puntos en la recta real y estudiamos los signos en los intervalos (paso 4):

Escogemos los puntos \(x=1\) del primer intervalo, \(x =3\) del segundo intervalo y \(x=8\) del tercero:
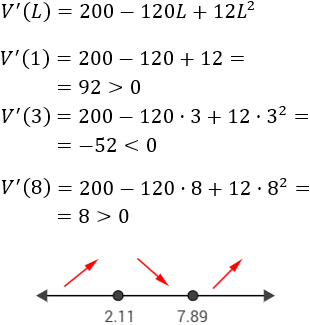
Luego la función es creciente en el primer intervalo, decreciente en el segundo y creciente en el tercero:
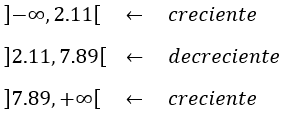
Pero el lado \(L\) debe medir entre 2 y 3, es decir, debe ser
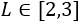
Como en el intervalo \([2.11, 3]\) la función es decreciente, el volumen será máximo para \(L=2.11cm\).
Por tanto, las dimensiones de la caja deben ser

Es decir, las dimensiones son 15.78 x 5.78 x 2.11 cm y su volumen es \(192.45 cm^2\).
Problema 2
Una empresa vende 0.7 toneladas de zumo y 0.3 toneladas de sobrante por cada tonelada de materia prima. El coste de la materia prima es de 0.8€/kg, los precios de venta del zumo y del sobrante son 2.5€/kg y 0.05€/kg, respectivamente, y el coste de producción viene dado por la función
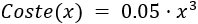
donde \(x\) representa las toneladas de zumo producido.
Obtener:
Una expresión para calcular las ganancias netas en función de las toneladas de materia prima.
-
La cantidad de zumo que se debe fabricar para que las ganancias netas sean máximas.
Solución
Sea \(x\) la cantidad de materia prima y sean \(z\) y \(s\) las cantidades de zumo y de sobrante, respectivamente.
El número de toneladas de zumo producido en función de las toneladas de materia prima es
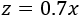
Y el de sobrante,
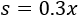
Las ganancias brutas son:
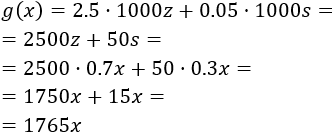
Hemos multiplicado por 1000 porque el precio es por kilo y no por tonelada.
El coste total es el coste de la materia prima más el coste de producción:
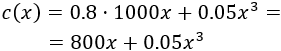
Luego las ganancias netas en función de las toneladas de materia prima son:
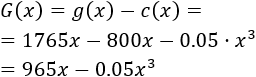
Calculamos la derivada:
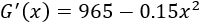
Igualamos la derivada a 0 y resolvemos la ecuación para buscar puntos críticos:
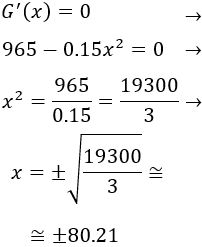
Representamos los puntos obtenidos en la recta real y estudiamos el signo de la derivada:

Elegimos el punto \(x=-100\) del primer intervalo, el punto \(x = 0\) del segundo y el punto \(x =100\) del tercer intervalo:

Por el criterio de la primera derivada, la función es decreciente en el primer y tercer intervalo y creciente en el segundo:
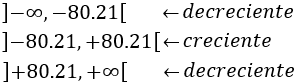
Nota: podemos acotar el dominio de la función al intervalo de los reales positivos ya que no tiene sentido que se produzcan cantidades negativas de zumo.
De la monotonía, deducimos que en el punto \(x=-80.21\) la función tiene un mínimo y en el punto \(x = 80.21\) tiene un máximo.
Por tanto, las ganancias netas son máximas cuando la cantidad de materia prima es 80.21 toneladas. En toneladas de zumo, equivale a 56.15 toneladas ya que
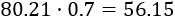
Problema 3
Una empresa de fabricación de puertas de madera utiliza un tablón rectangular para la hoja y tres listones de 10cm de ancho para el marco (lados laterales y lado superior). El precio del tablón es de $128 por metro cuadrado y el de los listones es de $87 por metro lineal.
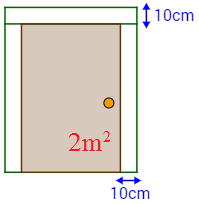
Calcular:
Las dimensiones de una puerta de \(2m^2\) de superficie de hoja para que el coste sea mínimo. ¿Cuál será su precio?
Si la puerta es de 2.5 metros de ancho y 0.8 metros de alto, ¿cuál es su precio?
Solución
Sean \(x\) e \(y\) la anchura y altura de la hoja de la puerta, respectivamente. Como la superficie de la hoja es \(2m^2\), tenemos que
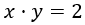
Como la anchura de los listones es de 10cm, la longitud del listón del lado superior debe ser (escribimos 0.1 ya que los precios son por metro)
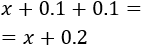
La longitud de los dos listones de los lados laterales debe ser
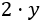
El coste total es el coste de la hoja más el del marco. El coste de la hoja es
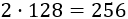
El coste del listón superior es
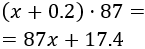
Y el coste de los listones laterales es
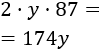
Por tanto, el coste total es
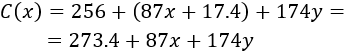
Como tenemos dos variables, escribimos \(y\) en función de \(x\):
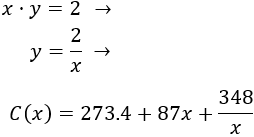
Calculamos la derivada:
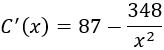
Igualamos a 0 y resolvemos la ecuación para buscar los puntos críticos:
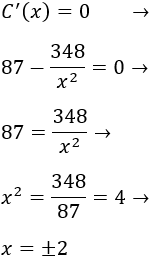
Situamos los puntos críticos en la recta real y estudiamos el signo de la derivada en los 4 intervalos:

Nota: hay que incluir el punto \(x=0\) como punto crítico ya que la función no está definida en dicho punto (no se puede dividir entre 0).
Escogemos \(x=-3\) para el primer intervalo, \(x=-1\) para el segundo, \(x=1\) para el tercero y \(x=3\) para el cuarto:
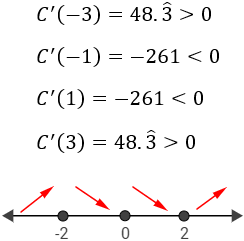
La función es creciente para \(x\leq -2\), decreciente en el intervalo \([-2,2]\) y creciente para \( x\geq 2\). Además, tiene un en \(x=2\).
Nota: cuando \(x\) tiende a \(-\infty\) la función decrece, pero como \(x\) representa una longitud, debe ser positiva.
Las dimensiones son
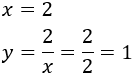
Es decir, 2 metros de ancho y 1 de alto.
Calculamos el coste:
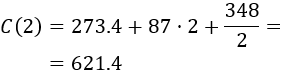
Luego el coste total de la puerta es $621.4.
Apartado b:
Evaluando la función en (\(x = 2.5\)),
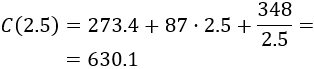
Problema 4
Encontrar parejas de números \(x\) e \(y\) tales que \(y\) sea el doble del cuadrado de \(x\) y que la resta de sus cuadrados (\(x^2 - y^2\)) sea máxima.
Solución
Sean \(x\) e \(y\) los números que buscamos. Como uno debe ser el doble del cuadrado del otro,
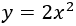
La resta de sus cuadrados es
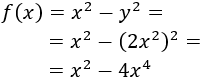
Derivamos la función:
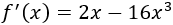
Igualamos la derivada a 0 y resolvemos la ecuación para encontrar los puntos críticos:
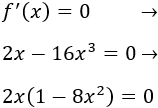
Una solución es \(x=0\). Las otras dos soluciones son
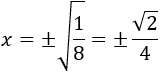
Representamos los puntos críticos en la recta real:

Estudiamos el signo de la derivada en cada intervalo. Escogemos los puntos \(x = \pm 1, \pm 0.1\):

De izquierda a derecha, la función es creciente, decreciente, creciente y decreciente.
Deducimos de la monotonía de \(f\) que tiene máximos en los puntos
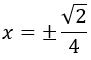
Calculamos \(y\) para cada \(x\):
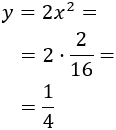
Las dos parejas encontradas son
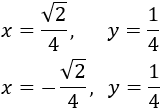
Problema 5
Las ganancias diarias en miles de dólares de una empresa petrolera son
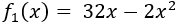
si \(0\leq x < 15\) y
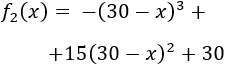
si \(x\geq 15\), siendo \(x\) el número de barriles de 1000L que se producen.
Calcular cuántos barriles deben producirse para maximizar las ganancias teniendo en cuenta que no se pueden extraer más de 35000L diarios.
Solución
Calculamos la derivada de las dos funciones:
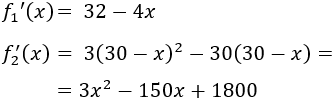
Igualamos ambas funciones a 0 para buscar los puntos críticos:
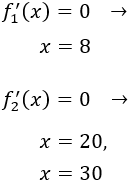
Representamos la recta real y los tres puntos críticos y estudiamos el signo de la derivada (teniendo en cuenta que en \(x=15\) cambia la función, por lo que añadimos también este punto):

Para estudiar el signo tomamos los puntos arbitrarios 5, 10, 16, 25 y 32:
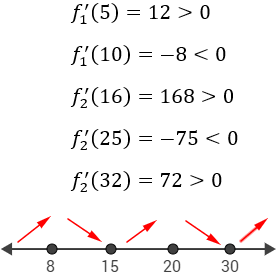
Luego, de izquierda a derecha, la función es creciente, decreciente, creciente, decreciente y creciente.
Los puntos críticos \(x = 8\) y \(x=20\) son máximos, pero tenemos que tener en cuenta que a partir de \(x=30\) la función es creciente.
Como no se pueden extraer más de 35000L diarios, debemos exigir que \(x\leq 35\).
Al ser la función creciente en el intervalo \([30, 35]\), también tenemos que considerar \(x = 35\) como un máximo.
Al tener tres máximos, debemos calcular el valor de la función en cada uno de ellos para escoger el mayor:
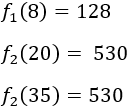
Por tanto, las ganancias son máximas cuando se producen 20 ó 35 barriles.
Problema 6
Una empresa está trazando parcelas iguales y rectangulares sobre el plano de un terreno para construir chalets de \(200m^2\) de superficie. Según la legislación de la zona, entre el chalet y la valla de la parcela debe haber un margen de 3 metros en los lados verticales y uno de 10 metros en los lados horizontales.
Calcular las dimensiones que deben tener las parcelas para que su área sea mínima. ¿Cuál será el área de una parcela?
Solución
Sean \(x\) e \(y\) las longitudes de los lados de la parcela (sin contar los márgenes), siendo \(x\) el lado horizontal.
El lado horizontal de la parcela, \(x\), más el margen lateral izquierdo y el margen lateral derecho mide
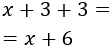
El lado vertical de la parcela, \(y\), más el margen superior y el margen inferior debe medir
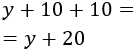
Como la superficie de la construcción debe medir \(200m^2\) sin contar los márgenes,
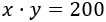
de donde podemos obtener \(y\) en función de \(x\):
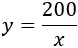
La función área de la parcela es
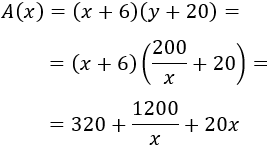
Como \(x\) está en el denominador, tenemos que exigir que sea distinto de 0.
Derivamos la función:
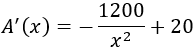
Igualamos a 0 la derivada y resolvemos la ecuación para encontrar los puntos críticos:
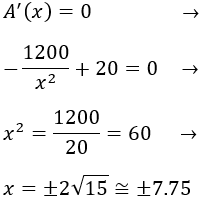
Representamos la recta real con los puntos críticos y el punto \(x=0\) (ya que en \(x=0\) la función no está definida):

Estudiamos el signo de la derivada en cada intervalo. Nosotros escogemos los puntos \(x=-8\), \(x=-1\), \(x=1\) y \(x=8\):
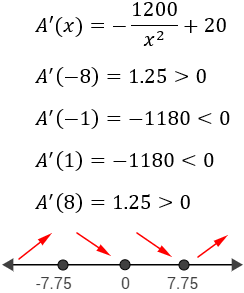
Sólo hay un mínimo y está en la parte de los reales positivos que es la que nos interesa (ya que la longitud debe ser positiva).
Por tanto,
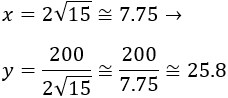
Para calcular las dimensiones de la parcela tenemos que sumar los márgenes.
El lado horizontal de la parcela (con márgenes) mide
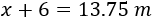
Y el lado vertical (con márgenes) mide
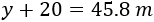
Luego las dimensiones de la parcela deben ser 45.8 x 13.75 metros y su área total es \(629.75m^2\).
Problema 7
Se desea colocar un cartel publicitario rectangular en el hueco que hay debajo de un puente cuya forma viene dada por la parábola
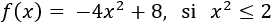
El cartel debe sujetarse por sus dos vértices superiores y la distancia entre el cartel y el suelo debe ser de 3m:
Calcular las dimensiones del cartel para que su área sea máxima y los puntos de los vértices superiores del cartel.
Solución
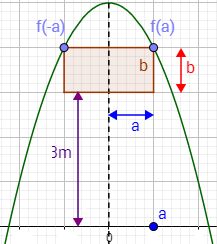
Hemos llamado \(a\) a la mitad de la anchura del cartel y \(b\) a la altura del cartel.
Nota: la función es simétrica respecto del eje de las ordenadas.
Tal y como se muestra en la imagen,
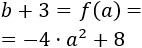
De la expresión anterior podemos escribir \(b\) en función de \(a\):
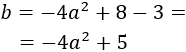
La función área del cartel es
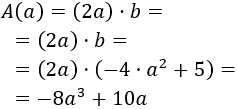
Derivamos la función área:
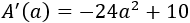
Igualamos a 0 para buscar los puntos críticos:
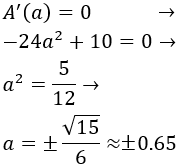
Situamos los puntos críticos en la recta real y estudiamos el signo de la derivada en los intervalos:

Escogemos \(a=-1\) para el primer intervalo, \(a=0\) para el segundo y \(a=1\) para el tercero:
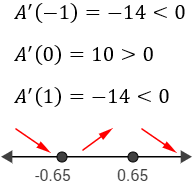
De izquierda a derecha, la función es decreciente, creciente y decreciente.
Por tanto, tiene un máximo en \(a=0.65\).
Con lo que la anchura del cartel debe ser
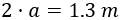
y la altura,
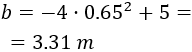
Como la parábola es simétrica, los vértices superiores del cartel son

Problema 8
Para fabricar un depósito cilíndrico de agua se necesitan materiales distintos para las bases y el lateral. El precio por metro cuadrado del material de las bases es de $2 y el del lateral es de $15.
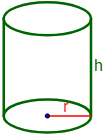
Calcular la altura \(h\) y el diámetro \(d=2r\) para que el coste de un depósito de 10 mil litros de capacidad sea mínimo. ¿Cuál es el precio del depósito?
Solución
Tendremos que utilizar las fórmulas del área y del volumen de un cilindro. Sean \(r\) el radio y \(h\) su altura.
El volumen se calcula fácilmente multiplicando el área de la base (que es un círculo) por su altura:
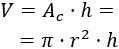
El área de la superficie es el área de las bases más el área del lateral. Como las bases son dos círculos de radio \(r\), sus áreas suman
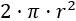
El lateral es un rectángulo de altura \(h\) y cuya base coincide con el perímetro de la base del cilindro, así que su área es
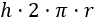
Por tanto, el área total del cilindro es
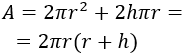
Como los precios de los materiales del cilindro son por metro cuadrado, la unidad de medida que utilizaremos será el metro.
La capacidad del cilindro debe ser 10000L. Sabiendo que un litro equivale a \(1dm^3\), la capacidad ha de ser de 10 000 \(dm^3\). Es decir,
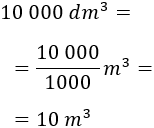
Igualamos el volumen del cilindro a su capacidad:
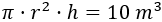
El precio del material es de $2 por metro cuadrado de base. Como hay dos bases, la cantidad asciende a
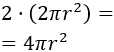
Y como el precio del lateral es de $15 por metro cuadrado, éste asciende a
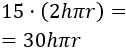
Luego la función precio del cilindro (del depósito) es
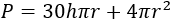
Podemos escribir \(h\) en función de \(r\):
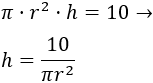
Así, la función es
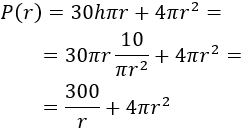
Derivamos la función:
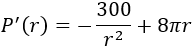
Igualamos a 0 y resolvemos la ecuación para encontrar los puntos críticos:
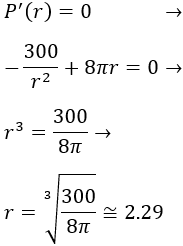
Representamos la recta real con el único punto crítico:
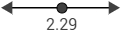
Ahora estudiamos el signo de la derivada en cada intervalo. Nosotros escogemos los puntos \(r=1\) y \(r=3\):
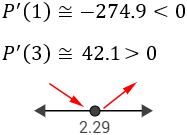
Luego la función tiene un mínimo en \(r=2.29\).
Por tanto, el radio debe medir 2.29m y la altura
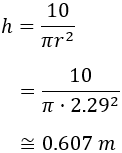
El precio del depósito nos lo proporciona la función:
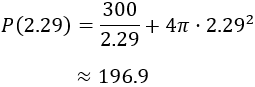
El precio del depósito es $196.9.
Problema 9
Se desea construir una mesa con la siguiente forma

siendo \(L\) la longitud del ancho del rectángulo y \(R\) el radio del extremo semicircular.
El precio del cristal a medida con forma rectangular es de $90 por metro cuadrado. Sin embargo, el precio del cristal con corte circular viene dado por la función
$$ Coste(R) = 150·R^2 $$
Calcular las medidas de la mesa de \(6m^2\) para que el coste sea mínimo bajo la condición \(1\leq R\leq 2\) y comentar el resultado obtenido.
Solución
La altura de la mesa (h) coincide con el diámetro del semicírculo:
El área de la parte rectangular es
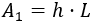
Y el área del semicírculo es
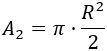
Luego la fórmla del área total de la mesa es
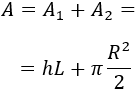
Como el área de la mesa ha de ser de \(6m^2\), tenemos que
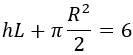
De esta relación podemos aislar el producto \(hL\):
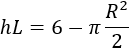
Para calcular el coste de la parte rectangular tenemos que utilizar el área del rectángulo (porque el precio es por metro cuadrado). Su coste es
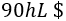
En cambio, el coste del semicírculo es función del radio es
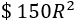
El coste total es
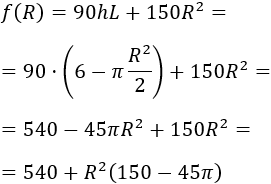
La derivada de la función es
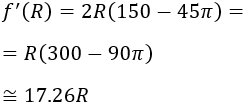
Igualamos a 0 la derivada y resolvemos la ecuación:
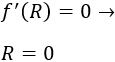
La función \(f\) es decreciente en los negativos y creciente en los positivos. Por tanto, el coste de la mesa será mínimo cuando \(R\) tome el menor valor (no negativo) posible.
Luego el radio de la mesa debe ser \(R=1m\).
Calculamos la altura y la anchura de la mesa:
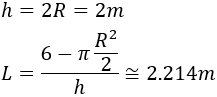
El coste de la mesa es $548.62:
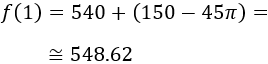
Como comentario, podemos decir que el mínimo encontrado no se corresponde con un mínimo propio de la función (de los que anulan la primera derivada), sino del extremo de definición del radio \(R\).
Como el coste de la parte semicircular de la mesa es mucho mayor que el de la parte rectangular, minimizar el coste sin restricciones implica fabricar la mesa sin la parte semicircular.
Problema 10
Se inscribe un rectángulo de base \(b\) y altura \(h\) en una circunferencia de radio \(r\). Si el centro del rectángulo coincide con el de la circunferencia, calcular sus lados en función del radio \(r\) para que su área sea máxima.
¿Cuál es el área del rectángulo?
Ayuda: algunos ejemplos de rectángulos inscritos del modo indicado en el enunciado son
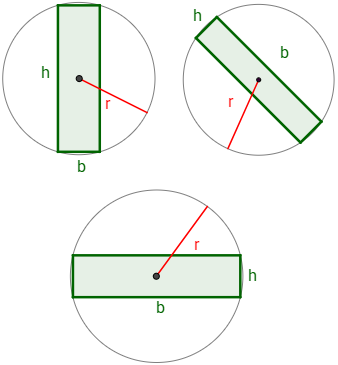
Solución
El área del rectángulo es
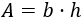
Como el centro del cuadrado coincide con el de la circunferencia, sus diagonales miden lo mismo que el diámetro, es decir, miden dos veces el radio:
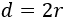
Al representar una de las dos diagonales se obtienen dos triángulos rectángulos iguales. Por tanto, podemos aplicar el Teorema de Pitágoras para escribir la altura \(h\) en función del lado \(b\) y del radio:
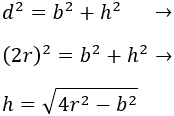
Así, el área del rectángulo es
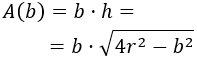
De este modo, el área es función de la base (el radio \(r\) no es una variable).
Derivamos la función área:
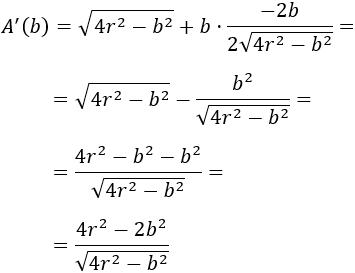
Nótese que para que el radicando sea positivo debe exigirse
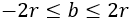
Pero como \(b\) es una longitud, debe ser positiva, así que
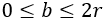
Igualamos a 0 la derivada y resolvemos la ecuación para encontrar los puntos críticos:
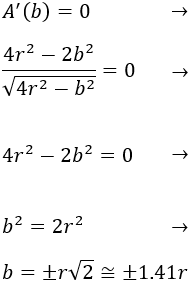
Por tanto, tenemos dos puntos críticos. Sólo situamos el positivo en la recta real y estudiamos el signo de la derivada. Utilizamos \(b= r\) y \(b= 1.5r\):
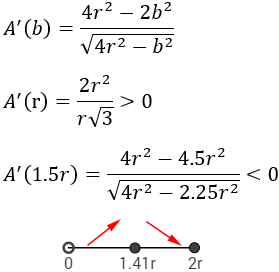
Nota: Hemos acotado la recta al intervalo de los valores que puede tomar \(b\).
Luego la función es creciente en el intervalo de la izquierda y decreciente en el de la derecha.
Por tanto, el punto \(b = r\cdot \sqrt{2}\) es un máximo.
La altura del rectángulo debe ser
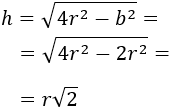
Para que el área sea máxima, la base y la altura deben medir \( r\cdot \sqrt(2)\), es decir, se trata de un cuadrado de lado \(r\cdot \sqrt(2)\). Su área es
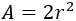
Problema 11
Encontrar dos números tales que la suma de uno de ellos con el cubo del otro sea 108 y que su producto sea lo más grande posible.
Solución
Sean los números \(x\) e \(y\). El hecho de que la suma de uno de ellos con el cubo del otro es 108 se representa del siguiente modo:
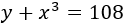
de donde podemos obtener \(y\) en función de \(x\):
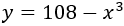
Nota: hemos escrito \(y+x^3\) en lugar de \(x+y^3\) para que al aislar \(y\) en función de \(x\) no tengamos que escribir la raíz cúbica (así los cálculos serán más simples).
La función producto es
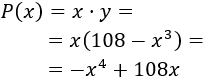
Derivamos la función:
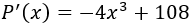
Igualamos a 0 la derivada y resolvemos la ecuación:
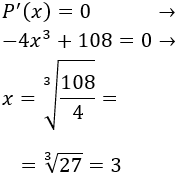
Representamos el punto crítico en la recta real:
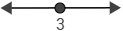
Estudiamos el signo de la derivada en ambos intervalos. Utilizaremos los puntos \(x=0\) y \(x= 4\):
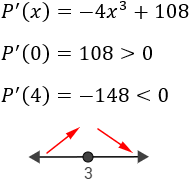
Por tanto, la función \(P\) es creciente en el intervalo \(]-\infty, 3[\) y decreciente en el intervalo \(]3, +\infty[\). De la monotonía se deduce que en \(x=3\) hay un máximo. Calculamos \(y\):
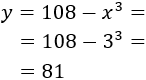
Por tanto, los números son \(x=3\) e \(y =81\) y su producto es \(x\cdot y = 243\).
Problema 12
Se desea construir una mesa de madera de 3 metros cuadrados con la siguiente forma:
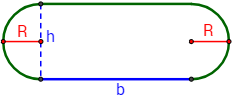
La mesa está formada por un rectángulo de lados \(b\) y \(h\) y en los lados que miden \(h\) hay adosados dos semicírculos de igual radio \(R\).
Si el precio de la madera es de 120€ por metro cuadrado y el coste del biselado de los bordes de la mesa es de 5€ por decímetro para los bordes rectos y 11€ por decímetro para los bordes curvos, calcular las dimensiones de la mesa (\(b\) y \(h\)) para que su coste sea mínimo.
Solución
Como el precio de la madera es por superficie y la superficie es de 3 metros cuadrados, el coste de la madera es
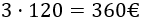
Si \(R\) es el radio de los semicírculos (son iguales), el lado \(h\) del rectángulo es
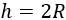
El área total de la mesa es la suma del área de un círculo de radio \(R\) y la del rectángulo:
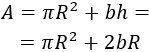
Como el área debe ser 3 metros cuadrados, podemos escribir el lado \(b\) en función del radio \(R\):
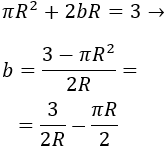
El coste total de la mesa es la suma de los costes de:
la madera (son 360€);
el biselado de los bordes rectos, es decir, de los dos lados \(b\);
el biselado de los dos semicírculos. Esto equivale al biselado del borde de un círculo.
Como el área es en metros cuadrados, tenemos que escribir el coste de cada biselado en metros:
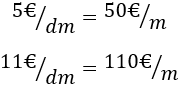
Por tanto, el coste de la mesa en función del radio \(R\) es
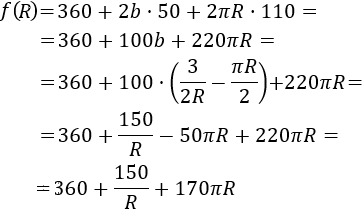
Nótese que \(R\) debe ser no nulo.
Derivamos la función:
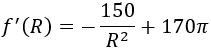
Igualamos a 0 la derivada y resolvemos la ecuación:
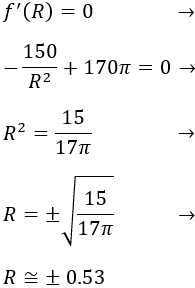
Ahora representamos los puntos críticos en la recta real y estudiamos el signo de la derivada.
Como el radio debe ser positivo, estudiamos el signo en los dos intervalos de la derecha.
Escogemos los puntos \(R = 0.1\) y \(R =0.6\):
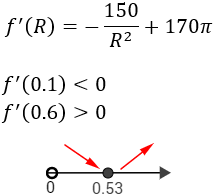
Como la función decrece y luego crece, tiene un mínimo en \(R=0.53\).
Calculamos los lados óptimos de la mesa (\(h\) y \(b\)):
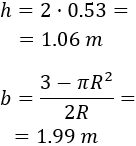
Luego las dimensiones de la mesa son 1.06 x 1.99 metros y su coste es 926.07€:
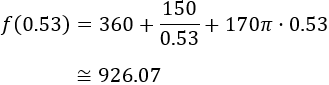
Problema 13
De entre todos los rectángulos con igual perímetro, ¿cuál es el de mayor área?

Solución
Sean \(x\) e \(y\) los lados del rectángulo. Su perímetro es
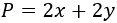
Como el perímetro es fijo, podemos obtener \(y\) en función de \(x\):
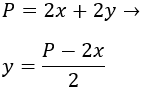
Así, su área en función del lado \(x\) es
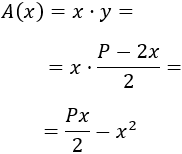
Calculamos la derivada:
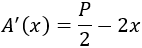
Igualamos a 0 para encontrar los puntos críticos:
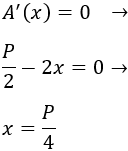
Situamos el punto crítico en la recta real y estudiamos el signo de la derivada en los dos intervalos:
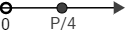
Nota: como \(x\) debe ser positivo, hemos acotado la recta real a los positivos.
Evaluamos la derivada en los puntos arbitrarios \(P/6\) y \(P\) para estudiar su signo:
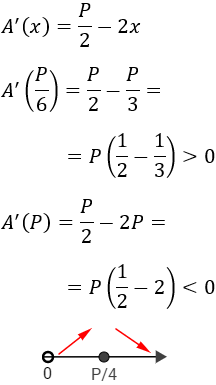
Como la función es creciente en el intervalo izquierdo y decreciente en el derecho, en \( x=P/4\) tiene un máximo.
Sustituimos \(x\) para calcular \(y\):
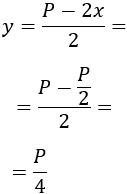
Luego \(x=y\). Por tanto, de entre todos los rectángulos con el mismo perímetro, el cuadrado es el de mayor área.
Problema 14
Se inscribe un triángulo en una circunferencia de radio \(r = 1\) y centro el origen del plano cartesiano. Si los vértices del triángulo son \((0,r)\), \((x,y)\) y \((-x,y)\) (los tres están sobre la circunferencia), calcular los vértices del triángulo de área máxima. ¿Cuál es su área? ¿Es un triángulo equilátero o isósceles?
Solución
La ecuación de una circunferencia de radio 1 centrada en el origen es
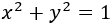
Si despejamos la \(x\), tenemos dos funciones:
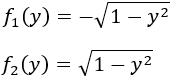
Las gráficas de las funciones \(f_1\) y \(f_2\) son las semicircunferencias izquierda y derecha, respectivamente.
El vértice \((0,1)\) del triángulo es fijo. Los otros dos son
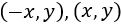
Por tanto, el triángulo es simétrico respecto del eje de ordenadas, por lo que podemos trabajar con la mitad derecha del triángulo. Nótese que, dependiendo de si \(y\) es positivo o negativo, las posibles mitades del triángulo son
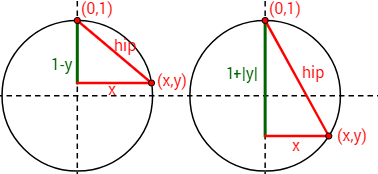
La mitad del triángulo es rectángulo y, como sus dos catetos miden \(x\) y \(h\), su área es
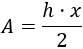
Por tanto, el área total del triángulo que buscamos es \(2\cdot A\).
En ambas figuras, las bases de los triángulos miden \(x\), pero como \(x\) depende de \(y\), cada uno de ellos tiene un valor que puede ser distinto.
La altura \(h\) del triángulo de la izquierda es \(h=1-y\) (en este caso \(y>0\)) y en el de la derecha es \(h=1+|y|=1-y\) (en este caso \(y<0\)). Por tanto, tanto si \(y\) es negativa como si es positiva (es decir, sea el triángulo que sea), la función área es
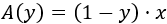
Vamos a buscar el máximo de la función área:
Como el punto \((x,y)\) está en la gráfica de \(f_2\), su primera coordenada es
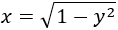
Así, el área es
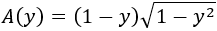
Derivamos la función:
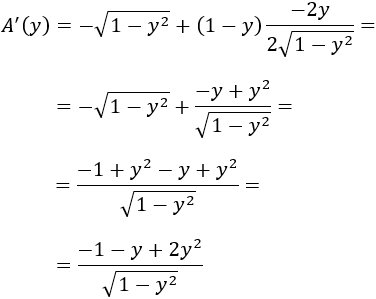
Nota: \(y\) debe ser distinto de \(\pm 1\).
Igualamos a 0 y resolvemos la ecuación:
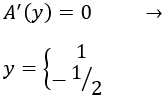
Representamos los puntos críticos en la recta real:

Nota: hemos acotado los intervalos según los valores que puede tomar \(y\).
Estudiamos el signo de la derivada:
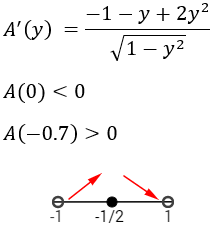
Hay un máximo en \(y=-1/2\). Calculamos \(x\):
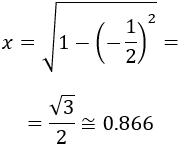
Luego los vértices del triángulo son
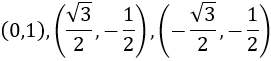
Y su área es
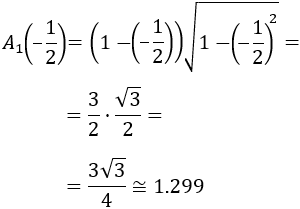
La base del triángulo mide
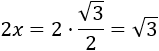
Los otros dos lados miden lo mismo por simetría. Veamos si su longitud coincide con la base:
La altura del triángulo mide
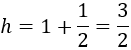
Aplicando Pitágoras, tenemos la medida \(a\) de los otros lados:
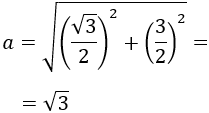
Los tres lados miden lo mismo, así que el triángulo es equilátero.
Problema 15
La siguiente figura representa el tronco y las dos ramas de un árbol (segmentos rojos) que mide 3 metros de altura. Se observa que cada año el tronco y las ramas crecen 1 metro (en la dirección que indican las flechas azules).
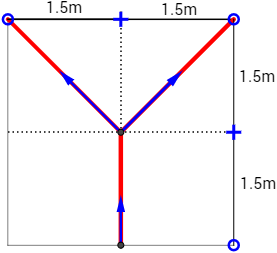
Calcular:
-
la altura del árbol en el instante \(t\),
-
la velocidad de crecimiento del árbol en función del tiempo y
-
la altura del árbol después de 24 años.
¿Cuándo alcanza el árbol su altura máxima?
Solución
Llamaremos \(x\) a la altura del árbol e \(y\) a su anchura. Inicialmente,
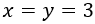
Si observamos la imagen, cada una de las ramas es la diagonal de un cuadrado de lado 1.5m. Aplicando Pitágoras, cada rama mide \(r\) siendo
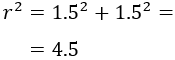
Por tanto, cada rama mide \(r =\sqrt{4.5}\).
Después de un año (\( t=1\)), el tronco mide un metro más y las ramas también miden 1 metro más. El crecimiento de un metro del tronco suma un metro a la altura, pero hemos de calcular cuánto suma en la altura del árbol el crecimiento de un metro de las ramas:
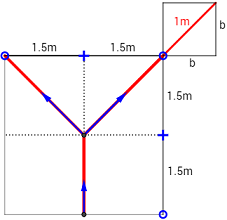
Por Pitágoras,
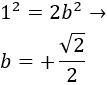
Por tanto, la altura total del árbol en función del tiempo (\(t\) años) es
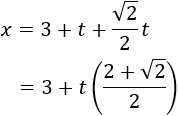
Luego la función de la altura en función del tiempo es
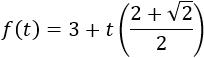
La velocidad de crecimiento es la derivada de la altura:
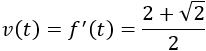
Es una velocidad constante.
Después de 24 años el árbol mide 43.97 metros:
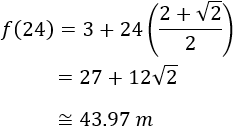
La derivada de la altura del árbol (velocidad de creciemiento) es constante y positiva. Por tanto, no existen puntos críticos y la función es monótona creciente.
La función altura no tiene máximos absolutos ni relativos mientras no se acote su dominio.
Problema 16
Encontrar los extremos relativos y absolutos (si los hay) de la función
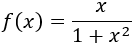
y obtener una función \(F(x)\) primitiva de \(f\) tal que \(F(2) = f(2)\).
Solución
Calculamos la derivada de \(f\) para buscar sus extremos:
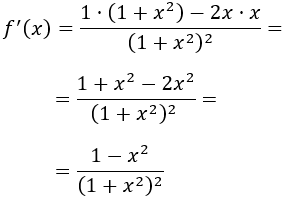
Igualamos a 0 la derivada y resolvemos la ecuación para encontrar los puntos críticos:
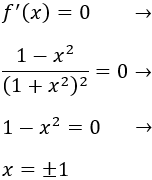
Representamos los puntos críticos en la recta real y estudiamos el signo de la derivada en los intervalos que determinan:

Utilizaremos los valores \(x=\pm 2\) y \(x=0\):
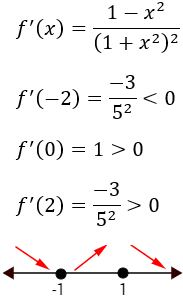
Por tanto, \(f\) es decreciente cuando \(x\leq 1\) y \(x\geq 1\) y creciente cuando \(-1<x<1\). Deducimos entonces que \(f\) tiene un mínimo en \(x=-1\) y un máximo en \(x =1\).
¿Es un mínimo absoluto?
-
Como la función decrece en el intervalo \(x\leq -1\) hasta llegar al mínimo, no puede haber valores de \(f\) que sean menores que el mínimo \(x=-1\) en dicho intervalo.
-
La función crece en el intervalo \(-1<x<1\) desde el mínimo, así que tampoco puede tomar valores menores que el mínimo en este intervalo.
-
Sin embargo, la función decrece en el intervalo \(x\geq 1\), así que sí podría haber valores menores que el mínimo si decrece indefinidamente.
Ahora bien, el límite de la función es
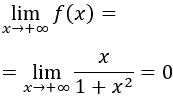
Esto significa que hay una asíntota horizontal en \(y = 0\) y como el mínimo es \(f(-1) = -0.5\), que toma un valor menor que la asíntota, el mínimo sí es un mínimo absoluto.
Razonando del mismo modo, la función sólo podría tomar valores mayores que el máximo (\(f(1)=1/2\)) en el intervalo \(x\leq -1\). Pero esto no se da puesto que hay una asíntota en \(y=0\) y la función toma valores por debajo de dicha asíntota:
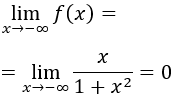
Gráfica:
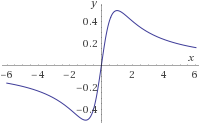
Nota: hemos cambiado la escala de la gráfica para apreciar la monotonía.
Para obtener una primitiva \(F\) de \(f\), integramos \(f\):
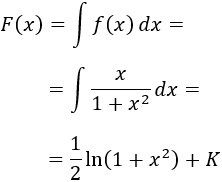
Buscamos la constante \(K\) para que \(F(2) = f(2)\):
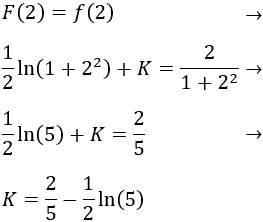
Problema 17
Encontrar dos números distintos \(a\) y \(b\) tales que uno de ellos sea el cubo del otro (\(b =a^3\) ) y la resta de sus cuadrados (\(a^2-b^2\)) sea máxima.
Razonar todos los pasos y enunciar los teoremas o resultados empleados.
Solución
Llamaremos a los números \(x=a\) e \(y=b\).
Como \(b\) es el cubo de \(a\),
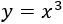
La resta de sus cuadrados es
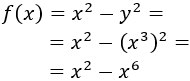
donde hemos escrito \(y\) en función de \(x\).
Como queremos que la diferencia de los cuadrados sea máxima, tenemos que buscar los máximos de la función \(f\). La derivada de \(f\) es
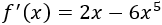
Por el Criterio de la primera derivada, la función \(f\) (continua y derivable en todos los reales) es monótona creciente en los puntos cuya derivada es positiva y es monótona decreciente en los puntos donde la derivada es negativa.
Los extremos (relativos o absolutos) de \(f\) anulan su derivada. Por tanto, los puntos candidatos a ser extremos (puntos críticos) son los que anulan a la derivada.
Buscamos los puntos críticos igualando a 0 la derivada:
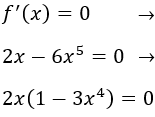
Un punto crítico es \(x=0\). Los otros son
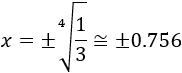
Situamos los puntos críticos en la recta real:

La función \(f'\) es continua por ser polinómica, así que su signo no varía dentro de cada uno de los intervalos

Por tanto, podemos saber el signo de \(f'\) en cada intervalo evaluando \(f\) en un punto arbitrario de cada uno de ellos:
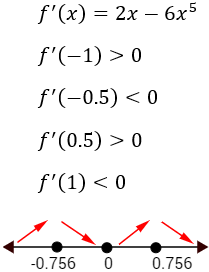
Por tanto, la función \(f\) es creciente en los intervalos \(I_1\) e \(I_3\) y decreciente en los intervalos \(I_2\) e \(I_4\).
Como consecuencia, en los puntos \(x=\pm 0.756\) hay máximos y en el punto \(x=0\) hay un mínimo.
Además, teniendo en cuenta que en los laterales (\(x \to \pm\infty\)) la función decrece, los máximos son absolutos.
El mínimo es relativo ya que
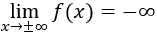
Los números buscados son
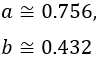
y también
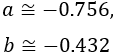
Nota: hemos escrito los números con aproximaciones. Exactamente, son
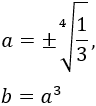
Problema 18
El trazado de una nueva carretera sobre el término municipal del pueblo A coincide con la gráfica de la función
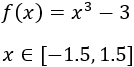
El ayuntamiento del pueblo A desea estudiar los puntos de la carretera más cercanos al pueblo para construir tiendas y los más lejanos para construir naves industriales. Así se consigue que todas las edificaciones tengan un rápido acceso desde la carretera y los ciudadanos tengan cerca las tiendas y lejos los ruidos de las industrias.
Encontrar todos los puntos óptimos para ambos tipos de construcciones según los criterios del ayuntamiento sabiendo que las coordenadas del pueblo son (0,0).
Ayuda: las únicas raíces reales del polinomio \(3x^4-9x+1\) son, aproximadamente, \(x_1 \simeq 0.11\) y \(x_2 \simeq 1.4\).
Solución
Como el pueblo está situado en el punto (0,0), debemos encontrar los máximos y los mínimos de la función distancia del pueblo a la carretera.
Recordamos que la distancia euclidiana entre los puntos \((x_1, y_1\)) y \((x_2, y_2)\) es
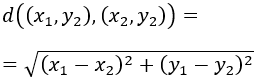
Así que la distancia entre el punto \((0,0)\) y el punto \((x,f(x))\) de la carretera es
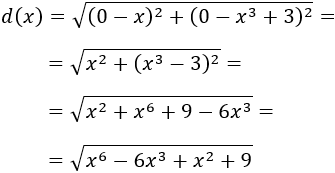
La derivada de la función es
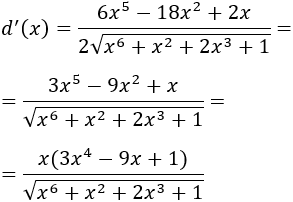
Igualamos a 0 la derivada y resolvemos la ecuación:
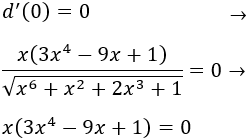
Por tanto, hay 3 puntos críticos: \(x_0=0\), \(x_1 \simeq 0.11\) y \(x_2 \simeq 1.4\). Los representamos en la recta real:

Nota: hemos acotado la recta ya que la función está definida en el intervalo \([-1.5,1.5]\).
Estudiamos el signo de la derivada en cada intervalo:
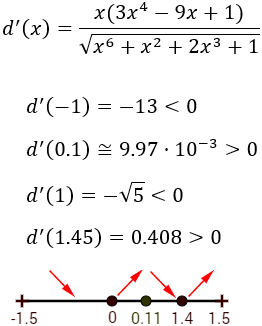
La función es decreciente, creciente, decreciente y creciente, respectivamente, en los intervalos de izquierda a derecha.
Hay máximos en \(x= \pm 1.5\) y \(x=0.11\) y mínimos en \(x=0\) y \(x=1.4\).
Por tanto, las coordenadas de los puntos para las tiendas son
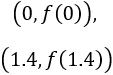
Y para las naves industriales son
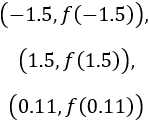
Problema 19
Calcular los extremos relativos y/o absolutos de la función \(f(x)=sin(2x)-x\) definida en el intervalo
$$I=\left] - \frac{\pi}{2}, \frac{\pi}{2}\right[ \subset\mathbb{R}$$
y calcular la integral definida de \(f\) en el intervalo \(I\).
Solución
La derivada de la función es
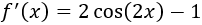
Igualamos a 0 la derivada y resolvemos la ecuación:
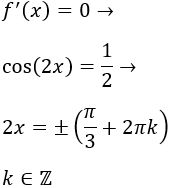
Nota: recuerda que la función seno es par (\(cos(x)=cos(-x)\)) y periódica (\(cos(x)=cos(x+2\pi k\))).
Los puntos críticos son
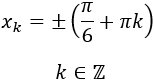
Pero tenemos que calcular los valores de \(k\) para los que \(x_k\) está en el intervalo \(I\):
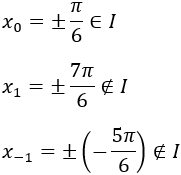
Luego el único valor para el que \(x_k\in I\) es \(k=0\). Por tanto, sólo tenemos dos puntos críticos:
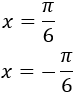
Representamos los puntos en el intervalo \(I\):

y estudiamos el signo de la derivada:
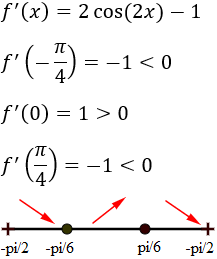
Por tanto, hay un mínimo en \(x=-\pi/6\) y un máximo en \(x=\pi/6\).
Para saber si son absolutos tenemos que ver si la función toma valores superiores e inferiores a los del máximo y mínimo, respectivamente.
Teniendo en cuenta la monotonía, los puntos donde esto puede ocurrir son los cercanos a los extremos del intervalo \(I\):
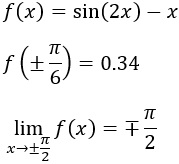
Nota: técnicamente, debemos calcular los límites ya que los puntos \(x=\pm \frac{\pi}{2}\) no son del dominio de \(f\).
Por tanto, los dos extremos no son absolutos.
La integral que se pide es
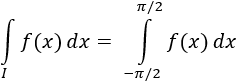
Primero calculamos la integral indefinida de \(f\):
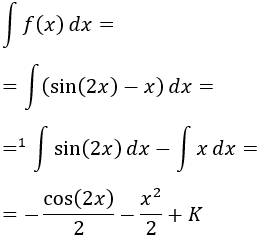
En la igualdad señalada con “1” hemos hemos tenido en cuenta que la integral de la suma es la suma de las integrales y que las constantes que multiplican al integrando pueden entrar y salir de la integral.
Aplicando la Regla de Barrow, la integral definida en \(I\) es 0:
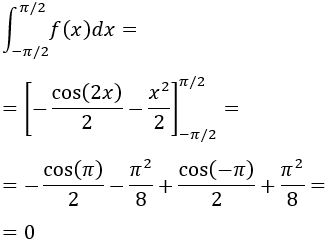
Problema 20
Demostrar que la sucesión \(a_n\) es monótona decreciente \(\forall n\in\mathbb{N}\) y calcular su límite (\( n\to +\infty\)).
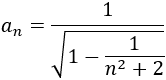
Solución
Nota: podemos considerar que la sucesión \(a_n\) está formada por puntos de una función \(f\). Esto es, \(a_n = f(n),\ n\in\mathbb{N}\). Entonces, si la función \(f\) es decreciente, la sucesión es decreciente.
Definimos la función
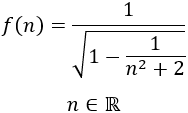
Nota: debemos considerar que \(n\) toma valores reales y no sólo naturales.
Para facilitar los cálculos, podemos escribir
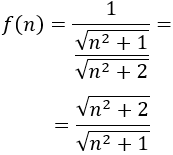
La derivada es
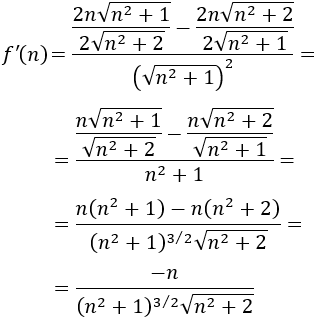
Por tanto, el único punto crítico es \(n=0\).
Como la función derivada es negativa cuando \(n\) toma valores naturales, la sucesión es decreciente.
Para calcular el límite, también utilizaremos la forma simplificada:
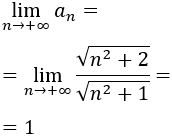
Nota: El grado del numerador y del numerador es 1 (ya que \(\sqrt{n^2} = n\)). Así que el límite es el cociente de los coeficientes directores:
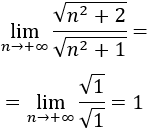
Problema 21 (dificultad alta)
Calcular de forma razonada todos los extremos relativos y/o absolutos de la siguiente función definida a trozos:
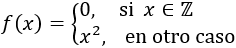
siendo \(\mathbb{Z}\) el conjunto de los números enteros:
$$ \mathbb{Z}=\{0, \pm 1, \pm 2, \pm 3,...\}$$
Solución
La derivada de la función es
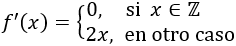
La derivada se anula en todos los enteros.
La función \(f\) es creciente en todos los intervalos del tipo \(]n,n+1[\) y decreciente en los intervalos \(]-n-1, -n[\) siendo \(n\in\mathbb{N}\). Es fácil de imaginar puesto que la función en dichos intervalos es la parábola \(f(x)=x^2\). En efecto, la derivada de la función en dichos intervalos es negativa si \(x< 0\) y positiva si \(x> 0\).
Pero los intervalos no son cerrados, es decir, los números enteros no están los intervalos. Como la función se anula en los enteros, son mínimos relativos todos los enteros.
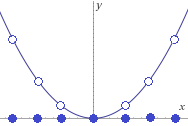
El único extremo absoluto es \(x=0\) puesto que la función crece indefinidamente hacia la izquierda y hacia la derecha de dicho punto.
La gráfica de la función es:
Problema 22
Demostrar que toda parábola \(y=ax^2+bx+c\) (con \(a\neq 0\)) tiene un máximo o mínimo absoluto y que su vértice se encuentra en el punto \(\left(-\frac{b}{2a},c-\frac{b^2}{4a}\right)\).
Solución
Toda parábola tiene un vértice y éste es un máximo absoluto o un mínimo absoluto.
Sea la función
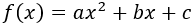
La derivada es
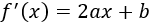
Igualamos la derivada a 0 y resolvemos la ecuación:
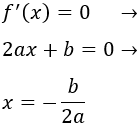
Sólo existe un punto crítico:
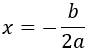
Ahora debemos demostrar que el punto crítico es, en efecto, un extremo ya que no todos los puntos críticos son extremos. Para ello, calculamos la segunda derivada:
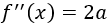
Evaluamos la segunda derivada en el punto crítico:
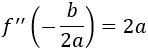
Si el parámetro \(a\) de la función es positivo, entonces
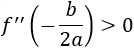
Y, por tanto, en el punto crítico hay un mínimo.
Si por el contrario \(a\) es negativo, en el punto crítico hay un máximo.
Para demostrar que los extremos son absolutos es suficiente calcular el límite
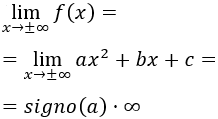
Es decir, el límite siempre tiende a infinito y el signo del infinito depende del signo del coeficiente \(a\).
La primera coordenada del vértice es
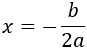
Y la segunda es
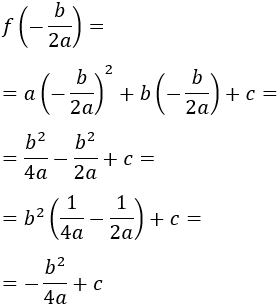
Es decir, el punto es
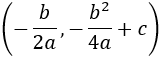
Problema 23
La función
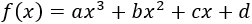
tiene un extremo en \(x=\pm 1\) y
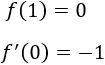
Calcular los coeficientes \(a,b,c\) y \(d\) y determinar si los extremos proporcionados son mínimos o máximos.
Solución
Evaluando \(f\) en \(x=1\) obtenemos una ecuación:
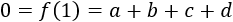
Calculamos la derivada de \(f\):
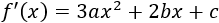
Evaluando la derivada en \(x=0\) obtenemos que \(c=-1\):
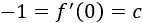
Luego la derivada de \(f\) es
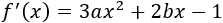
Sabemos de la existencia de dos extremos, así que la derivada se anula en dichos extremos:
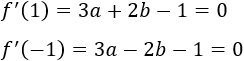
Sumando estas dos últimas ecuaciones podemos calcular el valor del coeficiente \(a\):
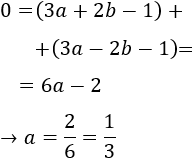
Sustituyendo en cualquiera de las dos ecuaciones anteriores se obtiene \(b=0\).
Finalmente, utilizamos la primera ecuación obtenida:
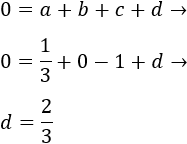
Los coeficientes son
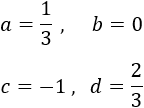
Y la función es
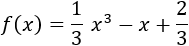
Como sólo queremos saber el tipo de dos extremos en concreto, usaremos el criterio de la segunda derivada.
Calculamos la segunda derivada:
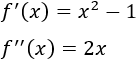
Evaluamos los puntos críticos::
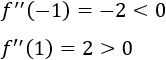
Por tanto, el extremo \(x=-1\) es un máximo y \(x=1\) es un mínimo.
La gráfica de la función es
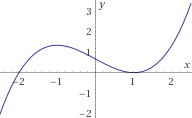
Problema 24
Sabiendo que la derivada de la función \(f\) es
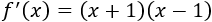
y que \(f(-1)=2\) :
Se pide:
calcular la función \(f\),
-
determinar si sus extremos son máximos o mínimos y
-
calcular la integral definida
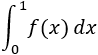
Solución
Para calcular la integral de la derivada, podemos escribirla como
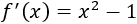
Así,
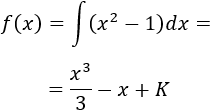
Para determinar el valor de \(K\) utilizamos el dato \(f(-1)= 2\):
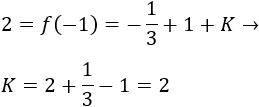
Por tanto, la función es
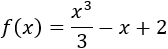
Igualamos la derivada a 0 para buscar los puntos críticos:
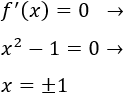
Estudiamos el signo de la derivada en cada intervalo. Escogemos los puntos \(x=\pm 2\) y \(x=0\):
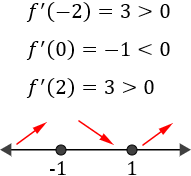
La función es creciente en los intervalos
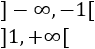
y decreciente en el intervalo
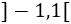
Por tanto, en \(x=-1\) tiene un máximo y en \(x=1\) tiene un mínimo.
Finalmente, calculamos la integral definida: