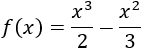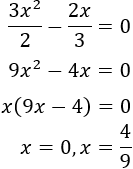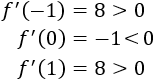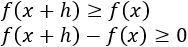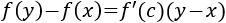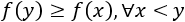Criterio de la primera derivada
En esta página enunciamos y demostramos el criterio de la primera derivada y proporcionamos un par de ejemplos de sus aplicaciones.
Contenido de esta página:
- Enunciado del criterio
- Aplicaciones del criterio
- Ejemplos de aplicación
- Demostración del criterio
Páginas relacionadas
Otras páginas:
1. Enunciado del criterio
Sea \(f\) una función continua en el intervalo \([a, b]\subset\mathbb{R}\) y derivable en \(]a, b[\). Entonces,
- La función \(f\) es monótona creciente en el intervalo \(]a,b[\) si, y sólo si, \(f'(x)\geq 0\) para todo \(x\in ]a,b[\).
- La función \(f\) es monótona decreciente en el intervalo \(]a,b[\) si, y sólo si, \(f'(x) \leq 0\) para todo \(x\in ]a,b[\).
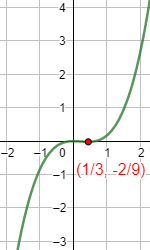
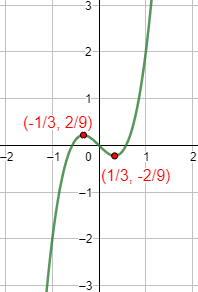
Decimos que \(c\in ]a,b[\) es un punto crítico si \(f'(c) = 0\).
Los puntos críticos son los candidatos a ser extremos relativos (y absolutos) de la función.