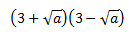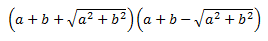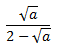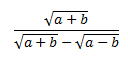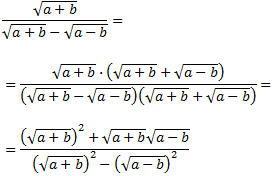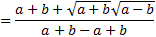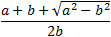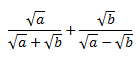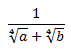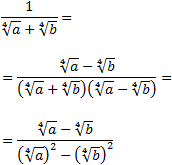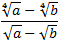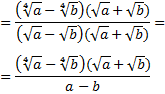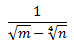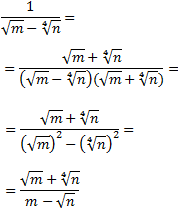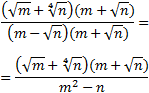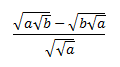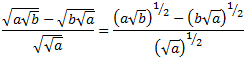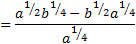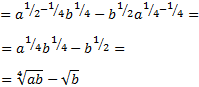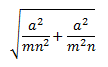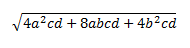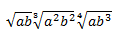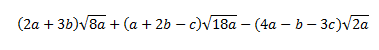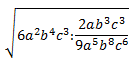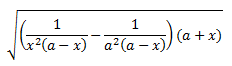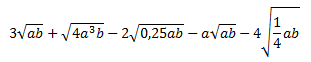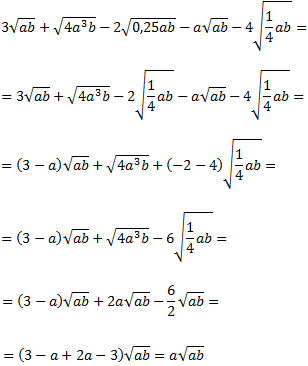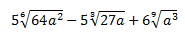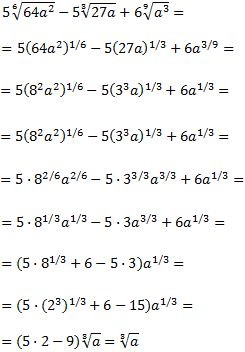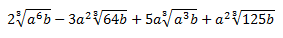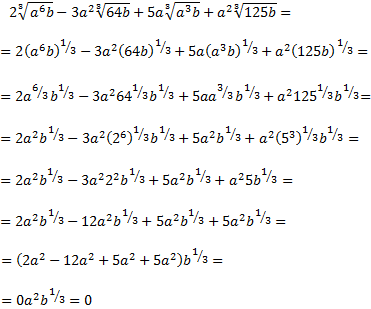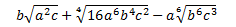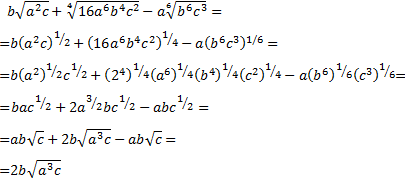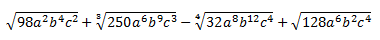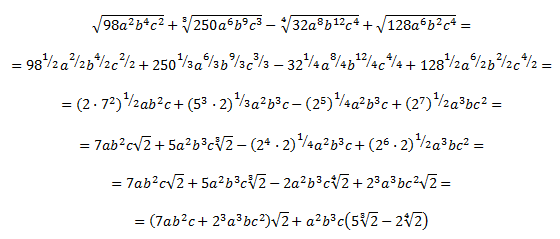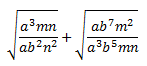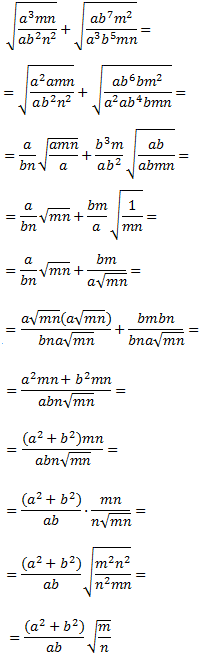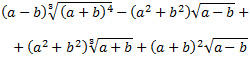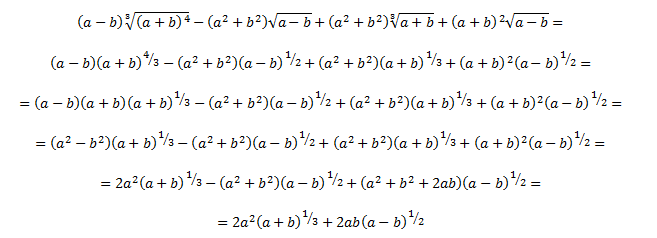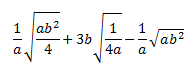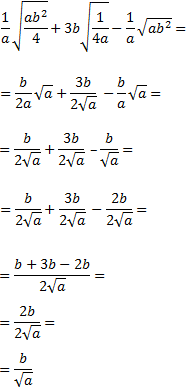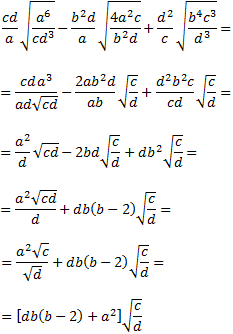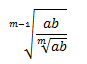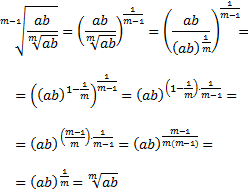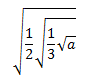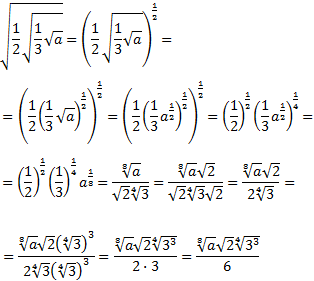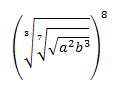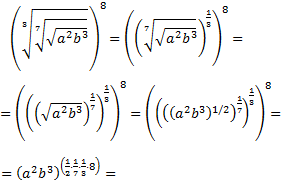En todos los ejercicios se considera que los parámetros son siempre positiivos.
Los dos primeros ejercicios son de calentamiento.
Ejercicio 1
Calcular el siguiente producto:
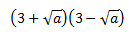
Solución
Tenemos un producto notable: suma
por diferencia es igual a la diferencia de los cuadrados:
$$(3+\sqrt{a})(3-\sqrt{a})=$$
$$ = 3^2-(\sqrt{a})^2 $$
La raíz cuadrada desaparece al elevarla al cuadrado:
$$ 3^2-(\sqrt{a})^2 = 9-a $$
Ejercicio 2
Calcular el siguiente producto:
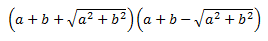
Solución
Podemos agrupar los sumandos del siguiente
modo para ver que en realidad tenemos una suma por diferencia
$$(a+b+\sqrt{a^2+b^2})(a+b-\sqrt{a^2+b^2})= $$
$$=\left((a+b)+\sqrt{a^2+b^2}\right)\left((a+b)-\sqrt{a^2+b^2}\right)$$
Por tanto, el producto es la diferencia de los cuadrados:
$$\left((a+b)+\sqrt{a^2+b^2}\right)\left((a+b)-\sqrt{a^2+b^2}\right)=$$
$$=(a+b)^2-\left(\sqrt{a^2+b^2}\right)^2=(a+b)^2-(a^2+b^2) $$
La raíz cuadrada ha desaparecido porque está elevada al cuadrado.
Ahora aplicamos la fórmula del cuadrado de la suma:
$$(a+b)^2-(a^2+b^2)=$$
$$ = a^2+b^2+2ab -(a^2+b^2)= $$
$$ = 2ab $$
En los siguientes 3 ejercicios vamos a racionalizar fracciones simples:
Ejercicio 3
Racionalizar:
$$ \frac{3}{1-\sqrt{3}} $$
Solución
Como tenemos una resta en el denominador, multiplicamos por el conjugado de la resta (el conjungado se calcula cambiando el signo negativo por el positivo):
$$ \frac{3}{1-\sqrt{3}} =$$
$$= \frac{3\cdot (1+\sqrt{3})}{(1-\sqrt{3})\cdot (1+\sqrt{3})} $$
En el denominador tenemos una suma por una diferencia. El resultado de esta operación es la diferencia de los cuadrados de los sumandos:
$$ \frac{3\cdot (1+\sqrt{3})}{(1-\sqrt{3})\cdot (1+\sqrt{3})} =$$
$$= \frac{3\cdot (1+\sqrt{3})}{1^2 -(\sqrt{3})^2} $$
La raíz desaparece al elevar al cuadrado:
$$= \frac{3\cdot (1+\sqrt{3})}{1 -3} = $$
$$ = \frac{3\cdot (1+\sqrt{3})}{-2}$$
Ejercicio 4
Racionalizar:
$$ \frac{1}{5+\sqrt{3}} $$
Solución
La fracción de este ejercicio es como la del ejercicios anterior, pero en lugar de un signo negativo tenemos uno positivo.
Porcedemos del mismo modo (multiplicamos por el conjugado del denominador):
$$ \frac{1}{5+\sqrt{3}} =$$
$$= \frac{1\cdot (5-\sqrt{3})}{(5+\sqrt{3})\cdot (5-\sqrt{3})} $$
En el denominador tenemos una suma por una diferencia:
$$ \frac{1\cdot (5-\sqrt{3})}{(5+\sqrt{3})\cdot (5-\sqrt{3})} =$$
$$= \frac{1\cdot (5-\sqrt{3})}{5^2 -(\sqrt{3})^2} $$
La raíz desaparece al elevar al cuadrado:
$$= \frac{1\cdot (5-\sqrt{3})}{25 -3} = $$
$$ = \frac{1\cdot (5-\sqrt{3})}{22} =$$
$$ = \frac{5-\sqrt{3}}{22} $$
Ejercicio 5
Racionalizar la siguiente fracción con parámetros:
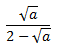
Solución
Como tenemos una resta en el denominador, multiplicamos por su conjugado:
$$ \frac{\sqrt{a}}{2-\sqrt{a}}= $$
$$= \frac{\sqrt{a}}{2-\sqrt{a}}\cdot \frac{2+\sqrt{a}}{2+\sqrt{a}} = $$
$$= \frac{\sqrt{a}(2+\sqrt{a})}{2^2-(\sqrt{a})^2}=$$
$$= \frac{2\sqrt{a}+(\sqrt{a})^2}{4-a} =$$
$$= \frac{2\sqrt{a}+a}{4-a} $$
La expresión final es un poco más larga que la inicial pero sin raíces en el denominador.
Ejercicio 6
Racionalizar la siguiente fracción que tiene una resta de raíces en el denominador:
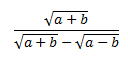
Solución
Como tenemos una resta en el denominador, multiplicamos por su conjugado:
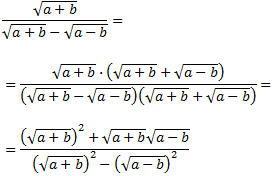
Las raíces cuadradas que están al cuadrado desaparecen:
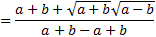
El denominador se simplifica fácilmente. En el numerador aplicamos la propiedad el producto de raíces es igual a la raíz del producto de sus radicandos y tenemos una suma por diferencia:
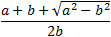
Ejercicio 7
Sumar las siguientes fracciones y racionalizar el resultado:
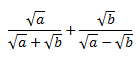
Solución
Para poder sumar las fracciones tienen que tener el mismo denominador. Nótese que el denominador de una de ellas es el conjugado de la otra.
El denominador común para poder sumar las fracciones es el producto de los denominadores:
$$ (\sqrt{a}+\sqrt{b})(\sqrt{a}-\sqrt{b}) $$
Multiplicamos y dividimos cada fracción por el factor que le falta al denominador para que ambas fracciones tengan el denominador común:
$$ \frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}} + \frac{\sqrt{b}}{\sqrt{a}-\sqrt{b}} =$$
$$= \frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}}\cdot \frac{\sqrt{a}-\sqrt{b}}{\sqrt{a}-\sqrt{b}} + \frac{\sqrt{b}}{\sqrt{a}-\sqrt{b}}\cdot \frac{\sqrt{a}+\sqrt{b}}{\sqrt{a}+\sqrt{b}} =$$
Sumamos las fracciones:
$$ = \frac{ \sqrt{a}\left(\sqrt{a}-\sqrt{b}\right) + \sqrt{b}\left(\sqrt{a}+\sqrt{b} \right)}{\left( \sqrt{a}+\sqrt{b}\right)\left( \sqrt{a}-\sqrt{b}\right)}=$$
Simplificamos el denominador, que es una suma por diferencia
$$ \left( \sqrt{a}+\sqrt{b}\right)\left( \sqrt{a}-\sqrt{b}\right) =$$
$$ = \left(\sqrt{a} \right)^2 -\left(\sqrt{b} \right)^2 = a-b $$
Y el numerador es
$$ \sqrt{a}\left(\sqrt{a}-\sqrt{b}\right) + \sqrt{b}\left(\sqrt{a}+\sqrt{b} \right) = $$
$$= (\sqrt{a})^2 -\sqrt{a}\sqrt{b} + \sqrt{b}\sqrt{a}+\left(\sqrt{b}\right)^2 =$$
$$= a -\sqrt{ab} +\sqrt{ab} +b = a+b$$
Por tanto,
$$ \frac{\sqrt{a}}{\sqrt{a}+\sqrt{b}} + \frac{\sqrt{b}}{\sqrt{a}-\sqrt{b}} =\frac{a+b}{a-b} $$
Ejercicio 8
Racionalizar la siguiente fracción que tiene una raíz cúbica en el denominador:
$$ \frac{2}{\sqrt[3]{5}} $$
Solución
La raíz del denominador es cúbica y, por tanto, si la multiplicamos ella misma, seguiremos teniendo una raíz en el denominador.
Al igual que las raíces cuadradas desaparecen cuando están al cuadrado, las raíces cúbicas desaparecen cuando están al cubo. Entonces, multiplicamos por la raíz al cuadrado:
$$ \frac{2}{\sqrt[3]{5}} =$$
$$ = \frac{2}{\sqrt[3]{5}} \cdot \frac{(\sqrt[3]{5})^2}{(\sqrt[3]{5})^2} = $$
$$ = \frac{2(\sqrt[3]{5})^2}{(\sqrt[3]{5})^3}$$
Desaparece el signo radical del denominador:
$$ = \frac{2(\sqrt[3]{5})^2}{5}$$
Si introducimos el cuadrado dentro de la raíz, el resultado final es
$$ \frac{2\sqrt[3]{25}}{5}$$
Ejercicio 9
Racionalizar la siguiente fracción que tiene una raíz séptima en el denominador:
$$ \frac{2}{\sqrt[7]{2}} $$
Solución
Multiplicamos y dividimos la fracción por la raíz del denominador elevada a la sexta para que desaparezca la raíz del denominador:
$$ \frac{2}{\sqrt[7]{2}} =$$
$$ = \frac{2}{\sqrt[7]{2}} \cdot \frac{(\sqrt[7]{2})^6}{(\sqrt[7]{2})^6} = $$
$$ = \frac{2(\sqrt[7]{2})^6}{(\sqrt[7]{2})^7}$$
Desaparece el signo radical del denominador:
$$ = \frac{2(\sqrt[7]{2})^6}{2} =$$
$$ = (\sqrt[7]{2})^6 = \sqrt[7]{64}$$
Ejercicio 10
Racionalizar la siguiente fracción que tiene una suma de raíces cuartas en el denominador:
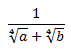
Solución
En los ejercicios anteriores las raíces eran cuadradas y por ello desaparecían al elevarlas al cuadrado. Sin embargo, no ocurre lo mismo cuando las raíces son de otro orden.
En esta fracción, el orden de las raíces es 4, por lo que tendremos que multiplicar por el conjugado dos veces:
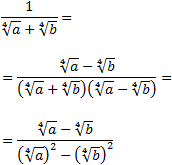
Recordad que las raíces son potencias con exponente fraccionario. Escribirlas de este modo puede ayudarnos en los cálculos. Si escribimos el cuadrado de raíz cuarta \(\sqrt[4]{a}\), tenemos
$$ (\sqrt[4]{a})^2 = \left( a^\frac{1}{4}\right)^2 =$$
$$ = a^\frac{2}{4} = a^\frac{1}{2} = \sqrt{a}$$
Del mismo modo,
$$ (\sqrt[4]{b})^2 = \sqrt{b} $$
Luego la fracción que queda es
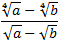
Finalmente, multiplicamos por el conjugado del denominador como en los ejercicios anteriores:
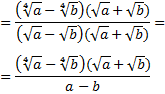
Ejercicio 11
Racionalizar la siguiente fracción con una diferencia de raíces de distinto orden en el denominador:
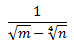
Solución
En esta fracción tenemos una raíz cuarta, así que tendremos que multiplicar dos veces por el conjugado del denominador para hacer que desaparezca:
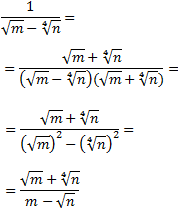
En el último paso hemos eliminado la raíz cuadrada porque estaba al cuadrado y la raíz cuarta al cuadrado se ha transformado en una raíz cuadrada. Si no vemos claro este segundo, podemos escribir la operación en forma de potencias:
$$ (\sqrt[4]{n})^2 = \left( n^\frac{1}{4} \right)^2 = $$
$$ = n^\frac{2}{4} = n^\frac{1}{2} = \sqrt{n} $$
Finalmente, multiplicamos y dividimos la fracción por el conjugado del denominador:
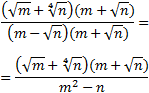
Ejercicio 12
Racionalizar la siguiente fracción con raíces de raíces (raíces anidadas):
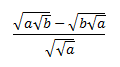
Solución
Como tenemos raíces de raíces, vamos a simplificar esta fracción escribiendo las raíces en forma de potencias. Recordad las propiedades de las potencias (producto y cociente de potencias y potencia de potencia).
Primero, escribimos las raíces exteriores como potencias con exponente \(1/2\) (porque son raíces cuadradas):
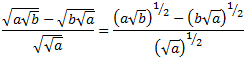
En el numerador aplicamos la potencia del producto es el producto de las potencias. En el denominador escribimos la raíz cuadrada como un potencia y tenemos una potencia de potencia, por lo que multiplicamos los exponentes:
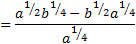
Para terminar, como tenemos en el denominador una potencia con base común, \(a\), podemos eliminarla al escribir su exponente restando al exponente de las potencias de \(a\) del numerador:
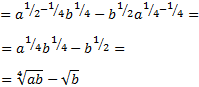
Ejercicio 13
Simplificar la siguiente raíz cuadrada racionalizando el resultado:
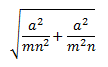
Solución
Antes de sumar las fracciones podemos extraer los factores comunes:
$$ \frac{a^2}{mn^2} + \frac{a^2}{m^2 n} = \frac{a^2}{mn}\left(\frac{1}{n} + \frac{1}{m} \right)= $$
$$ \frac{a^2}{mn}\left(\frac{m+n}{mn} \right) = \frac{a^2(m+n)}{m^2 n^2} $$
Por tanto,
$$\sqrt{\frac{a^2}{mn^2} + \frac{a^2}{m^2 n}} =$$
$$= \sqrt{\frac{a^2(m+n)}{m^2 n^2}} =\frac{a\sqrt{m+n}}{mn}$$
Hemos extraído de la raíz los factores del radicando que están al cuadrado. Los del numerador al numerador y los del denominador al denominador.
En los siguientes ejercicios se pide simplificar las expresiones al máximo, racionalizando el resultado si es necesario.
Ejercicio 14
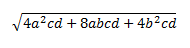
Solución
Empezaremos simplificando el radicando extrayendo factores comunes:
$$4a^2 cd + 8abcd + 4b^2 cd = $$
$$ = cd (4a^2 + 8ab + 4b^2) = $$
$$ = 4cd (a^2 + 2ab +b^2) $$
El paréntesis es el desarrollo del cuadrado de la suma a + b
$$ 4cd (a^2 + 2ab +b^2) = $$
$$ = 4cd (a+b)^2 = $$
$$ = 2^2 cd (a+b)^2 $$
Por tanto, la expresión inicial es igual a
$$ \sqrt{2^2 cd (a+b)^2} = 2(a+b)\sqrt{cd} $$
Hemos extraído de la raíz los factores que estaban al cuadrado.
Ejercicio 15
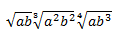
Solución
En este problema sólo tenemos que aplicar las propieades de las raíces (potencias):
-
Escribir las raíces como potencias
-
Escribir las potencias de los productos (es el producto de las potencias)
-
Multiplicar las potencias agrupándolas según la base (se suman los exponentes)
Escribimos las raíces como potencias:
$$ \sqrt{ab}\cdot \sqrt[3]{a^2 b^2} \cdot \sqrt[4]{ab^3} =$$
$$ = (ab)^{\frac{1}{2}} \cdot (a^2 b^2)^{\frac{1}{3}} \cdot (ab^3)^{\frac{1}{4}}=$$
$$ = a^{\frac{1}{2}} b^{\frac{1}{2}} a^{\frac{2}{3}} b^{\frac{2}{3}} a^{\frac{1}{4}} b^{\frac{3}{4}}$$
$$ = a^{\frac{1}{2}+\frac{2}{3} +\frac{1}{4}} \cdot b^{\frac{1}{2}+\frac{2}{3}+\frac{3}{4}} =$$
$$ = a^{\frac{17}{12}}b^{\frac{23}{12}} = \sqrt[12]{a^{17} b^{23}}=$$
$$ = a b\sqrt[12]{a^5 b^{11} } $$
Notemos que hemos escrito una a por cada 12 a que hay multiplicando en el radicando (quedan dentro 17 - 12 = 5). Igual para las b.
Ejercicio 16
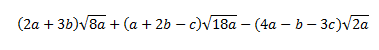
Solución
Vamos a intentar sumar todos los términos.
Notemos que tenemos la suma de tres raíces (en un principio distintas) y cada una tiene un coeficiente (el número que la multiplica).
Para poder agrupar los sumandos necesitamos que todos tengan la misma raíz, así que vamos a reescribirlas:
La primera raíz es
$$ \sqrt{8a} $$
Escribimos 8 como una potencia:
$$ \sqrt{8\cdot a} = \sqrt{2^3 \cdot a}= 2 \sqrt{2 \cdot a} $$
Recordemos que por cada cuadrado en el radicando podemos extraer una vez la base. Como teníamos 2 3 = 2 2 · 2 1, hemos extraído un 2 desapareciendo el cuadrado y quedando en el radicando 2.
La segunda raíz es
$$ \sqrt{18a} $$
Podemos escribir 18 en forma de producto de potencias como
18 = 2·9 = 2·3 2. Por tanto,
$$ \sqrt{18 \cdot a} = \sqrt{2\cdot 3^2 a } = 3 \sqrt{2a} $$
Notemos que la tercera raíz ya no la podemos simplificar más.
Ahora todos los sumandos tienen la misma raíz, por lo que
podemos sumarlos:
$$ (2a + 3b) 2 \sqrt{2a} + $$
$$ + (a+2b -c) 3 \sqrt{2a} - $$
$$ - (4a -b -3c) \sqrt{2a} = $$
$$= (4a + 6b) \sqrt{2a} + $$
$$ + (3a + 6b - 3c) \sqrt{2a} - $$
$$ - (4a -b -3c) \sqrt{2a} = $$
$$ = (4a + 6b + 3a + 6b -3c -4a +b +3c) \sqrt{2a} =$$
$$ = ( 13b + 3a ) \sqrt{2a} $$
Ejercicio 17
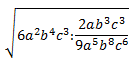
Solución
Lo primero que haremos es reducir el radicando. Una vez conseguido, escribiremos la raíz cuadrada. Así, será más rápido realizar los cálculos.
El radicando es
$$ 6a^2 b^4 c^3 : \frac{2ab^3 c^3 }{9a^5 b^8 c^6} $$
Antes de todo, diremos que la operación : (división) divide al producto que tiene a su izquierda entre la fracción que tiene a su dercha. No es necesario que haya paréntesis ya que no hay ninguna suma.
Escribimos esta división en forma de fracción ya que normalmente trabajamos más cómodamente con esta notación:
$$ 6a^2 b^4 c^3 : \frac{2ab^3 c^3 }{9a^5 b^8 c^6} =$$
$$ = \frac{6a^2 b^4 c^3}{ \frac{2ab^3 c^3 }{9a^5 b^8 c^6} } =$$
$$ = \frac{\frac{6a^2 b^4 c^3}{1}}{ \frac{2ab^3 c^3 }{9a^5 b^8 c^6} }$$
Hemos escrito el numerador de la fracción externa como una fracción para aplicar la regla mnemotécnica del sandwich: pan con pan y queso con queso. Esto quiere decir,
$$ \frac{\frac{a}{b}}{\frac{c}{d}} = \frac{a \cdot d}{b \cdot c} $$
Por tanto,
$$ \frac{\frac{6a^2 b^4 c^3}{1}}{ \frac{2ab^3 c^3 }{9a^5 b^8 c^6} } =$$
$$ = \frac{6a^2 b^4 c^3 9a^5 b^8 c^6 }{2ab^3 c^3 }$$
Simplificamos aplicando las reglas de las potencias (producto y división):
$$ \frac{6a^2 b^4 c^3 9a^5 b^8 c^6 }{2ab^3 c^3 } = $$
$$ = 27 a^6 b^9 c^6 $$
Por tanto, la expresión inicial (con la raíz) es igual a
$$ \sqrt{ 27 a^6 b^9 c^6} $$
Ahora escribimos los factores del radicando en forma de potencias
para poder extraer algunos:
$$ \sqrt{ 27 a^6 b^9 c^6} = $$
$$ = \sqrt{3 \cdot 3^2 a^2 \cdot a^2 \cdot a^2 \cdot b^2 \cdot b^2 \cdot b^2 \cdot b^2 \cdot b \cdot c^2 \cdot c^2 \cdot c^2} = $$
$$ = 3\cdot (a^3) \cdot (b^4)\cdot (c^3) \sqrt{3 \cdot b } $$
Notemos que el exponente de cada factor indica el número de potencias al cuadrado que hemos
extraído de la raíz cuadrada.
Podemos simplificar la expresión como
$$ = 3(ac)^3 b^4 \sqrt{3 \cdot b } $$
Ejercicio 18
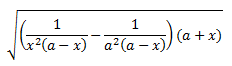
Solución
Trateremos de reducir la expresión del radicando sin escribir la raíz cuadrada para no arrastrar dicho símbolo durante las operaciones. Después la volveremos a escribir.
El radicando es el producto:
$$ \left( \frac{1}{x^2(a-x)} -\frac{1}{a^2(a-x)} \right)\cdot (a+x) $$
Para poder sumar las fracciones tienen que tener el mismo denominador, pero esto no es así.
En ambos denominadores tenemos el factor (a-x), pero en uno tenemos x2 y en el otro tenemos a2.
Multiplicamos y dividimos ambas cada una de las fracciones por el factor no común del denominador
de la otra fracción:
$$ \left( \frac{1}{x^2(a-x)} -\frac{1}{a^2(a-x)} \right)\cdot (a+x) = $$
$$ = \left( \frac{a^2 }{a^2 x^2(a-x)} -\frac{x^2 }{x^2 a^2(a-x)} \right)\cdot (a+x) $$
Ahora ya podemos sumar ambas fracciones obteniendo:
$$ \left( \frac{a^2 - x^2}{a^2 x^2(a-x)} \right)\cdot (a+x) $$
El numerador es una diferencia de cuadrados:
$$ a^2 -x^2 = (a+x)(a-x) $$
Entonces la expresión queda como
$$ \left( \frac{(a+x)(a-x)}{a^2 x^2(a-x)} \right)\cdot (a+x) =$$
$$= \left( \frac{(a+x)}{a^2 x^2} \right)\cdot (a+x) =$$
$$= \left( \frac{(a+x)^2}{a^2 x^2} \right) = $$
$$= \left( \frac{a+x}{a x} \right)^2 $$
Por tanto, la expresión inicial (con la raíz cuadrada) es igual a
$$ \sqrt{ \left( \frac{a+x}{a x} \right)^2} = $$
$$= \frac{a+x}{a x} $$
En los siguientes ejercicios ya no explicaremos todos los pasos.
Ejercicio 19
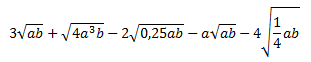
Solución
Ejercicio 20
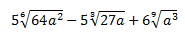
Solución
Ejercicio 21
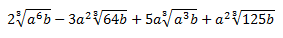
Solución
Ejercicio 22
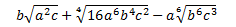
Solución
Ejercicio 23
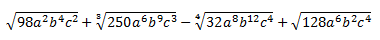
Solución
Ejercicio 24
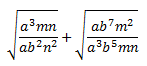
Solución
Ejercicio 25
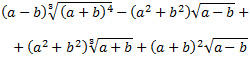
Solución
Ejercicio 26
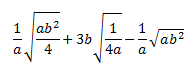
Solución
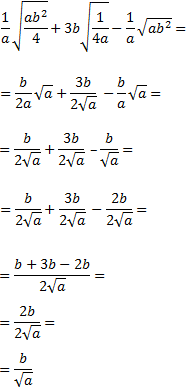
Al racionalizar se obtiene
$$ \frac{b\cdot \sqrt{a}}{a}$$
Ejercicio 27
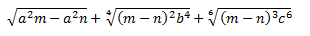
Solución
Ejercicio 28
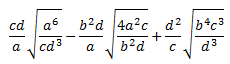
Solución
Ejercicio 29
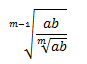
Solución
Ejercicio 30
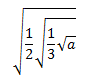
Solución
Ejercicio 31
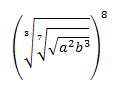
Solución
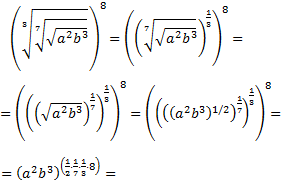
$$ = \sqrt[14]{a^2b^3}$$
Ejercicio 32
$$ \frac{x\sqrt{x} - a\sqrt{a}}{\sqrt{x}-\sqrt{a}} $$
Solución
Multiplicamos en el numerador y en el denominador por \(\sqrt{x}-\sqrt{a}\):
$$ \frac{x\sqrt{x} - a\sqrt{a}}{\sqrt{x}-\sqrt{a}} = $$
$$ = \frac{x\sqrt{x} - a\sqrt{a}}{\sqrt{x}-\sqrt{a}} \cdot \frac{\sqrt{x}+\sqrt{a}}{\sqrt{x}+\sqrt{a}}= $$
$$= \frac{x^2 + x\sqrt{ax} - a\sqrt{ax}-a^2}{x-a} =$$
$$= \frac{x^2-a^2 +\sqrt{ax}(x-a)}{x-a} =$$
$$ = \frac{(x+a)(x-a) +\sqrt{ax}(x-a)}{x-a}$$
Los factores \((x-a)\) se pueden simplificar:
$$ \frac{(x+a)(x-a) +\sqrt{ax}(x-a)}{x-a} =$$
$$= \frac{(x+a)+\sqrt{ax}}{1} =$$
$$ = x+a+\sqrt{ax} $$
Por tanto,
$$ \frac{x\sqrt{x} - a\sqrt{a}}{\sqrt{x}-\sqrt{a}} = x+a+\sqrt{ax}$$