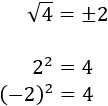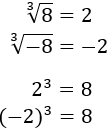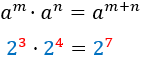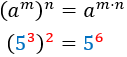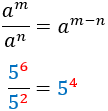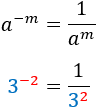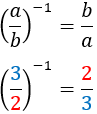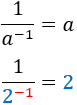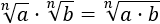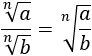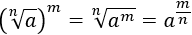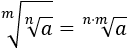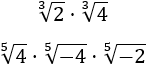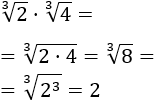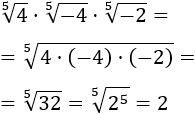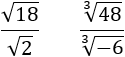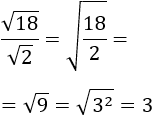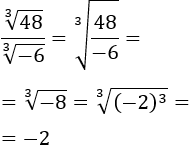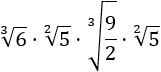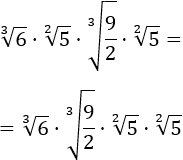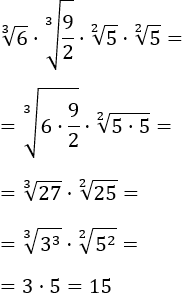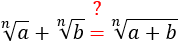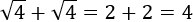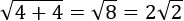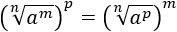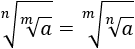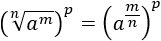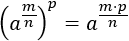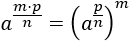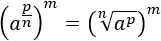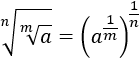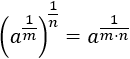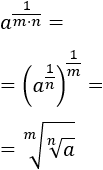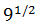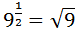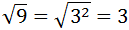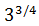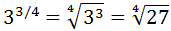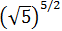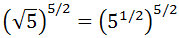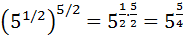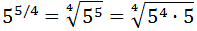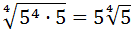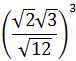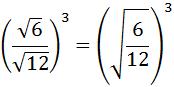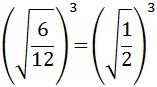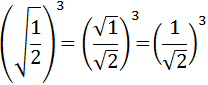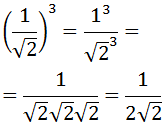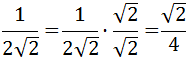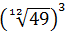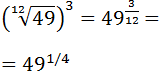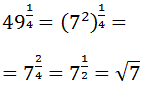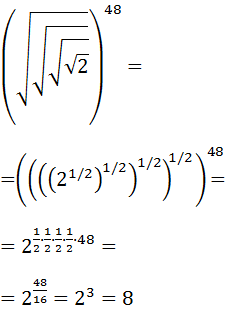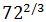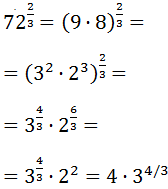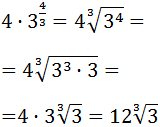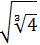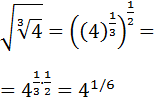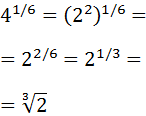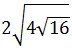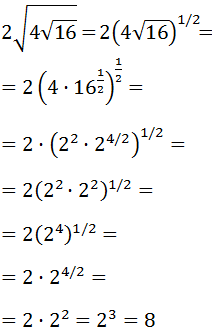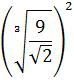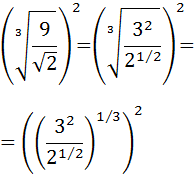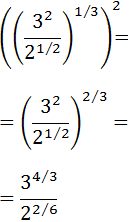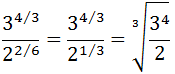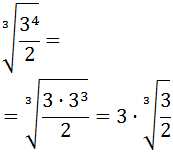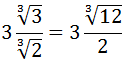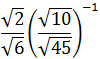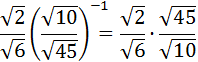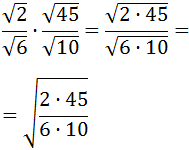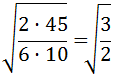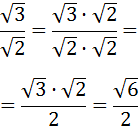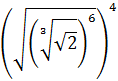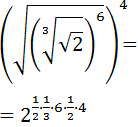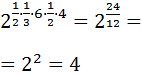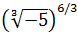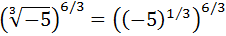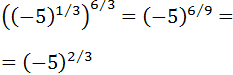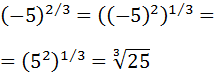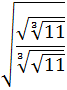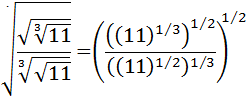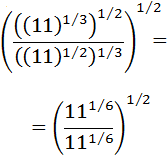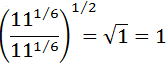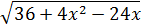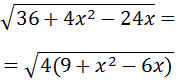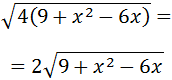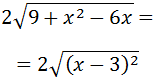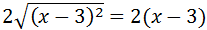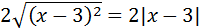Nota previa: cuando haya dos raíces, escribiremos sólo la positiva. En todos los ejercicios se tiene que simplificar el resultado.
Ejercicio 1 
Calcular los siguientes productos de raíces cúbicas y quintas:
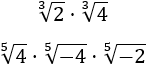
SOLUCIÓN:
Aplicamos la propiedad del producto de raíces: como son raíces del mismo orden, se multiplican sus radicandos.
Primer producto:
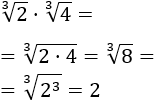
Observad que la raíz se cancela porque el radicando es una potencia con exponente 3 y el orden de la raíz es 3.
Segundo producto:
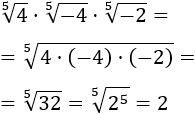
La raíz se cancela por la misma razón que en producto anterior.
Ejercicio 2 
Calcular los siguientes cocientes de raíces cuadradas y cúbicas:
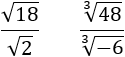
SOLUCIÓN:
Aplicamos la propiedad del cociente de raíces: como son raíces de igual orden, se dividen sus radicandos.
Primera división:
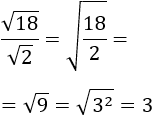
Segunda división:
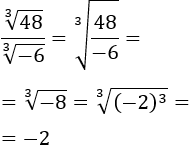
Ejercicio 3 
Calcular el siguiente cociente de raíces cuadradas y cúbicas:
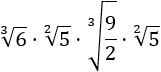
SOLUCIÓN:
Observad que no todas las raíces tienen el mismo orden.
Como tenemos un producto de raíces y el producto conmuta, podemos cambiar el orden:
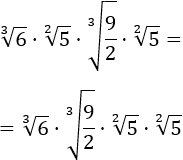
Así, podemos multiplicar las dos raíces de la izquierda y las dos de la derecha porque tienen el mismo orden:
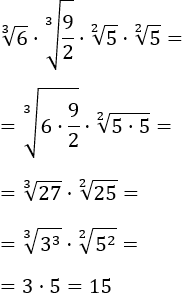
En el último paso no hemos multiplicado las raíces de orden distinto porque no era necesario, ya que las raíces se cancelan con las potencias de sus radicandos.
Ejercicio 4 
¿La suma de raíces de orden \(n\) es la raíz de orden \(n\) de la suma de sus radicandos?
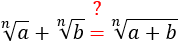
SOLUCIÓN:
La propiedad no es cierta. Veamos un contraejemplo (esto es, un ejemplo que lo niega):
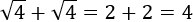
Sin embargo,
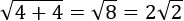
Ejercicio 5 
Demostrar las siguientes propiedades:
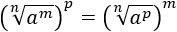
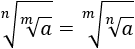
SOLUCIÓN:
Vamos a operar en el lado izquierdo hasta transformarlo en la expresión del lado derecho.
Propiedad 1:
Escribimos la raíz como una potencia:
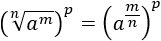
Multiplicamos los exponentes (potencia de potencia):
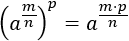
Hacemos el paso inverso (intercambiando el orden de los factores):
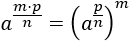
Escribimos la potencia como una raíz:
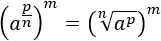
Propiedad 2:
Escribimos las raíces como potencias:
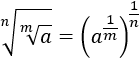
Multiplicamos los exponentes:
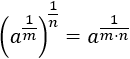
Ahora, cambiamos el orden de los factores y deshacemos el cambio:
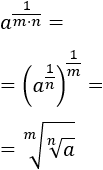
En adelante, lo que haremos es escribir las raíces como potencias con exponente fraccionario para aplicar las propiedades de las potencias.
Ejercicio 6 
Calcular la siguiente potencia:
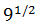
SOLUCIÓN:
Tenemos una raíz cuadrada escrita en forma de potencia:
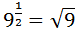
Sabemos que la raíz cuadrada de 9 es 3, pero podemos escribir 9 como \(3^2\) para dejar claro en la raíz cuadrada de un cuadrado se pueden eliminar la raíz y el exponente:
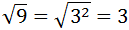
Nota: recordad que, en realidad, la raíz cuadrada de 9 es \(\pm 3\), pero en esta página sólo escribimos las raíces positivas.
Ejercicio 7 
Escribir la potencia como una raíz:
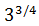
SOLUCIÓN:
Recordad la propiedad:
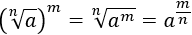
Como el denominador del exponente es 4, es una raíz de orden cuarto (raíz cuarta):
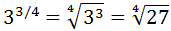
No podemos simplificar más la raíz.
Ejercicio 8 
Escribir la siguiente potencia como una raíz:
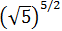
SOLUCIÓN:
Escribimos la raíz cuadrada como una potencia (con exponente 1/2):
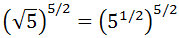
Como tenemos un potencia de una potencia, multiplicamos los exponentes:
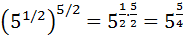
Escribimos la potencia como una raíz:
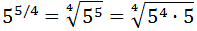
Como la raíz es cuarta, podemos extraer un 5 por cada \(5^4\) del radicando:
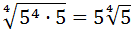
Ejercicio 9 
Simplificar:
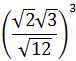
SOLUCIÓN:
Aplicamos la propiedad del producto de raíces del mismo orden:

Aplicamos la propiedad del cociente de raíces del mismo orden:
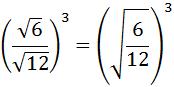
Simplificamos la fracción:
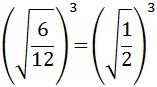
Simplificamos más:
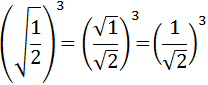
La potencia de un cociente es el cociente de sus potencias:
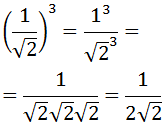
Podemos dejar el resultado así, pero a los matemáticos no nos gustan las raíces en los denominadores. Para evitar esto, multiplicamos y dividimos por la raíz del denominador:
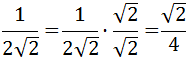
Ejercicio 10 
Escribir como una raíz:
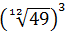
SOLUCIÓN:
Escribimos la raíz de orden doce como una potencia y simplificamos el exponente:
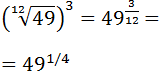
Observad que hemos pasado de una raíz de orden 12 a una de orden 4.
Escribimos el radicando, 49, como una potencia. Es decir, cambiamos 49 por \(7^2\). Así, podemos aplicar la propiedad de la potencia de una potencia:
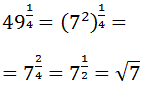
Ejercicio 11 
Calcular:
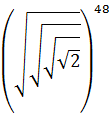
SOLUCIÓN:
Tenemos raíces cuadradas anidadas (unas dentro de otras). Vamos a escribir todas ellas como potencias con exponente 1/2. Así, podemos multiplicar los exponentes (potencia de una potencia):
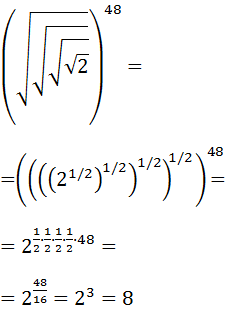
Ejercicio 12 
Escribir en forma de raíz:
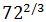
SOLUCIÓN:
Escribimos 72 como un producto de potencias para aplicar la propiedad de la potencia de un producto:
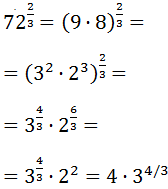
Escribimos la potencia fraccionaria como una raíz cúbica para
extraer algún factor:
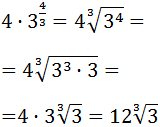
Observad que, como tenemos una raíz cúbica, podemos extraer un 3 por cada \(3^3\) del radicando (sólo había uno).
Ejercicio 13 
Escribir como una raíz:
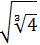
SOLUCIÓN:
Escribimos la raíz cúbica como una potencia con exponente \(1/3\) y la raíz cuadrada como una potencia con exponente \(1/2\):
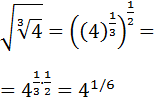
Escribimos el radicando, 4, como un potencia, \(2^2\):
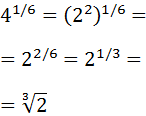
Ejercicio 14 
Calcular:
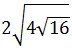
SOLUCIÓN:
Transformamos las raíces cuadradas en potencias y escribimos el número 4 como \(2^2\) y el número 16 como \(2^4\). Después, aplicamos las propiedades de las potencias:
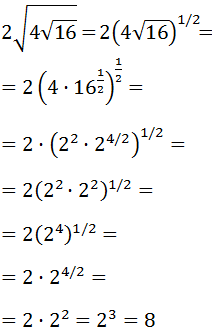
Ejercicio 15 
Simplificar:
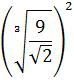
SOLUCIÓN:
Escribimos 9 como la potencia \(3^2\) y las raíces cúbica y cuadrada como potencias con exponentes \(1/3\) y \(1/2\):
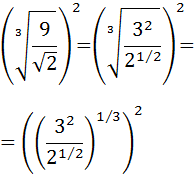
Como tenemos potencias de potencias, sólo tenemos que multiplicar los exponentes:
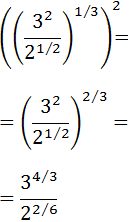
Simplificamos y escribimos como raíz:
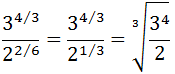
Hemos escrito el resultado como una raíz para extraer un factor de la raíz:
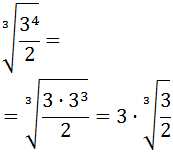
Si queremos, podemos seguir operando hasta llegar al resultado
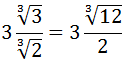
Ejercicio 16 
Calcular:
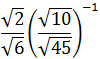
Solución
Recordad que la potencia -1 de una fracción es la fracción inversa (cambiar denominador por numerador):
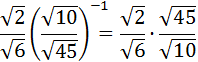
El producto de fracciones se calcula multiplicando entre sí los númeradores y los denominadores:
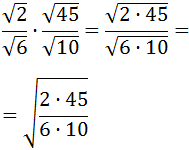
Simplificamos la fracción del radicando:
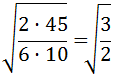
Eliminamos la raíz del denominador multiplicando y dividiendo por la raíz de 2:
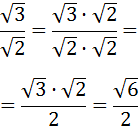
Ejercicio 17 
Calcular:
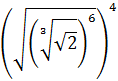
Solución
Sólo tenemos que escribir las raíces como potencias para multiplicar los exponentes (potencia de potencia):
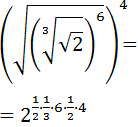
Simplificamos el exponente:
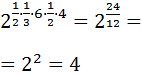
Ejercicio 18 
Escribir en forma de raíz:
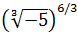
Solución
No es un problema que el radicando sea negativo poque la raíz es de orden impar.
Escribimos la raíz cúbica como una potencia:
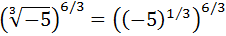
Multiplicamos los exponentes:
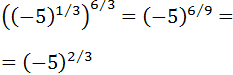
Podemos eliminar el signo negativo porque \((-5)^2 = 5^2\):
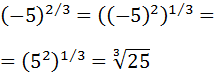
Ejercicio 19 
Calcular:
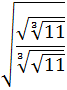
Solución
Escribimos las cinco raíces como potencias:
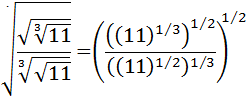
Multiplicamos exponentes:
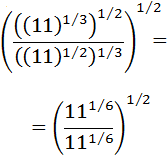
El cociente de potencias es 1 porque el numerador y el denomiandor son iguales:
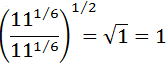
Ejercicio 20 
Simplificar:
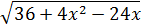
Solución
Podemos extraer 4 como factor común:
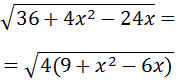
El 4 sale fuera de la raíz cuadrada como 2 porque es \(2^2\):
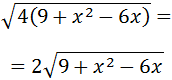
El radicando es el desarrollo del cuadrado de un binomio:
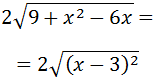
Finalmente, el cuadrado se cancela con la raíz cuadrada:
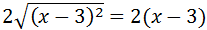
Nota: en realidad, deberíamos escribir valor absoluto al cancelar el cuadrado con la raíz porque el binomio podría tomar valores negativos:
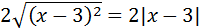


Propiedades de las raíces enésimas (raíces escritas como potencias), con ejercicios resueltos - © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.