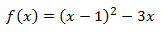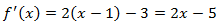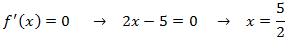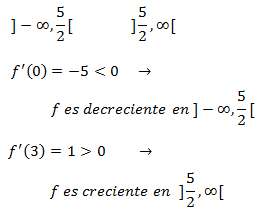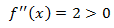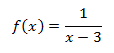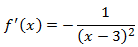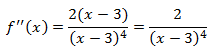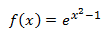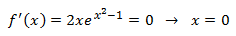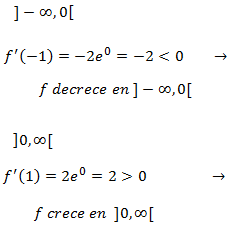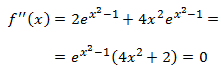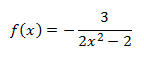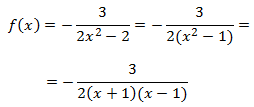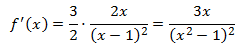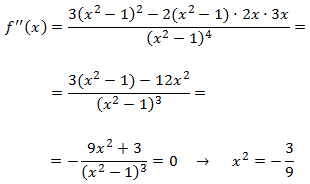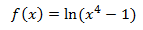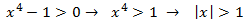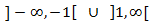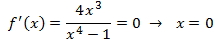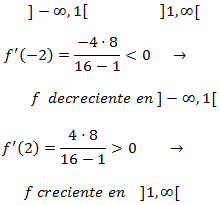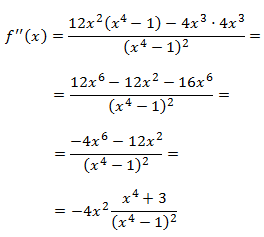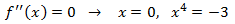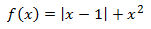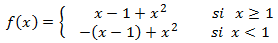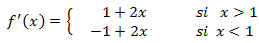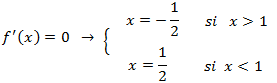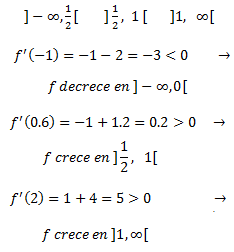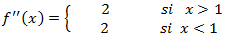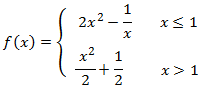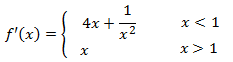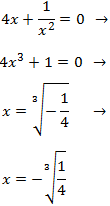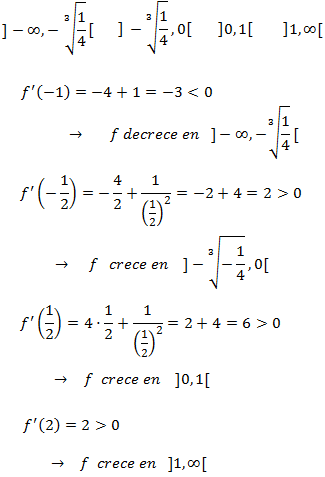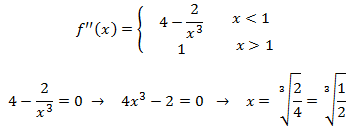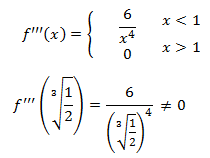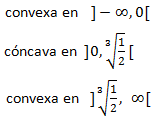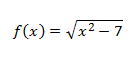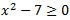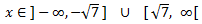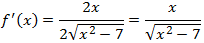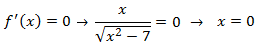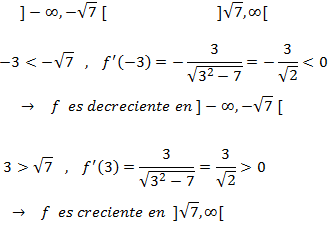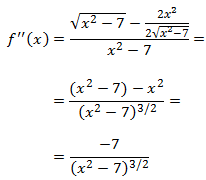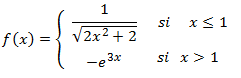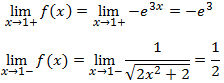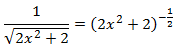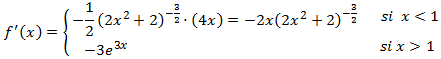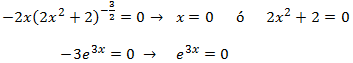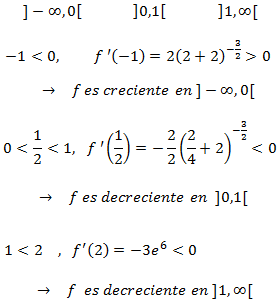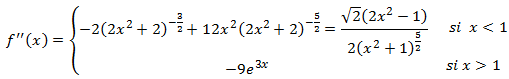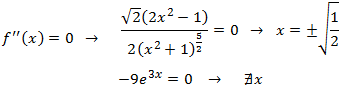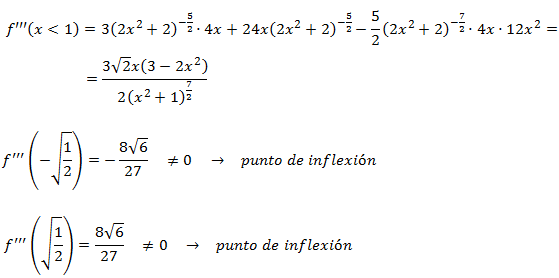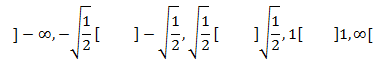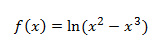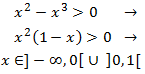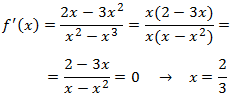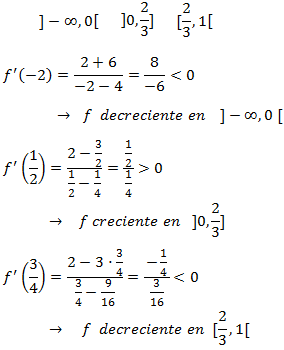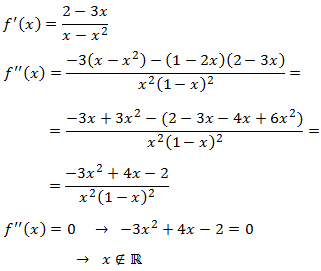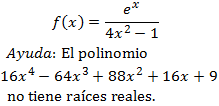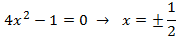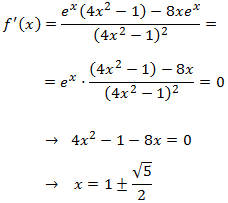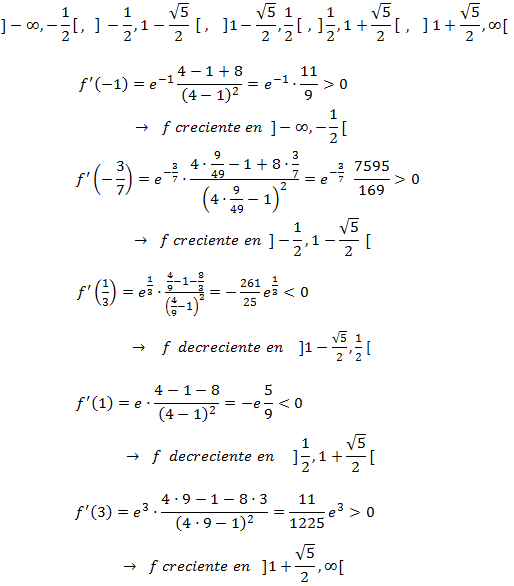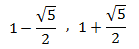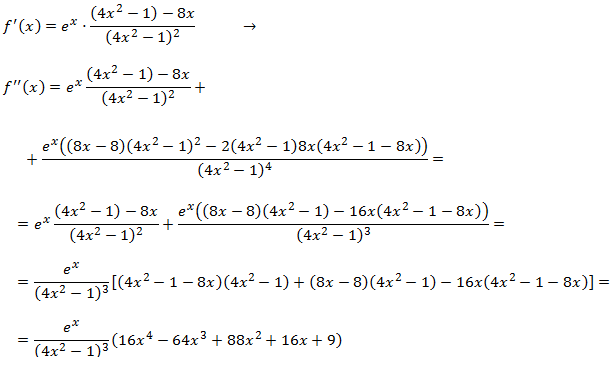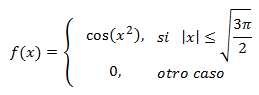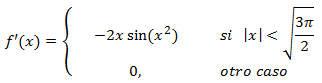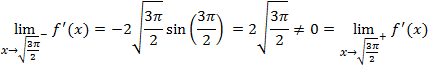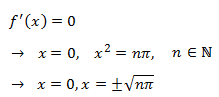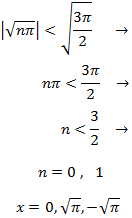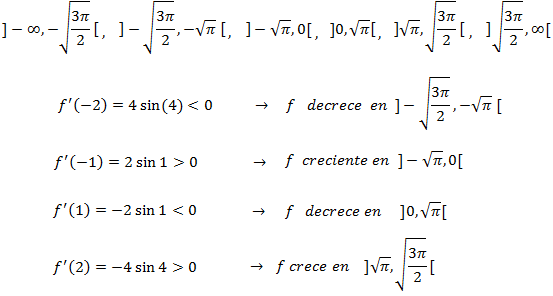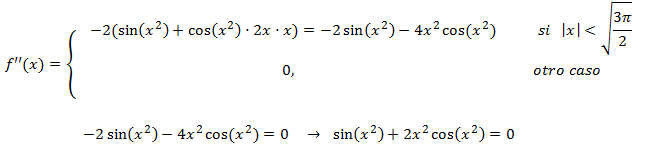Monotonía y Convexidad
Contenido de esta página:
Introducción
En esta sección estudiamos la monotonía y convexidad de funciones (reales y de una variable) mediante
ejemplos: funciones polinómicas, racionales, exponenciales, logarítmicas, con valores absolutos, definidas
a trozos, con raíces...
Respecto a la monotonía, buscaremos los intervalos en los que la función es
monótona creciente o decreciente aplicando el
criterio de la primera derivada, lo que nos permitirá deducir la
existencia de extremos (máximos y mínimos). También podemos usar el criterio de la segunda
derivada para determinar el tipo de extremo directamente.
Respecto a la convexidad, usaremos el criterio de la segunda derivada para buscar los
posibles puntos de inflexión. También podemos apoyarnos de la tercera derivada.
En cuanto a las aplicaciones prácticas de este estudio, podemos decir que, aparte de las aplicaciones
directas (conocer el comportamiento de la función), la monotonía nos permite demostrar ciertos resultados
(por ejemplo las relaciones de desigualdades entre dos expresiones).
Como comentario final, podemos comentar que el concepto de monotonía se extiende más allá de las funciones
de variable real. Un caso particular son los funcionales (funciones cuyas variables son funciones),
que se usan con frecuencia en el campo de la física.
Temas relacionados:
ejercicios de extremos de funciones,
cálculo de derivadas,
Regla de L'Hôpital.
Antes de empezar, haremos un resumen:
Método de resolución
- Estudiar el dominio de la función
- Si el dominio es los reales, los únicos posibles extremos son los puntos críticos, es decir, los que anulan la primera derivada.
- Si el dominio está formado por uno o más intervalos, tenemos que estudiar si los extremos finitos de los intervalos son extremos.
- Nota: si la función es a trozos, estudiamos cada intervalo del dominio como si fuese una única función y consideramos los extremos de éstos como posibles extremos.
- Búsqueda de extremos
- Calculamos la derivada de la función.
- Buscamos los posibles extremos: puntos críticos (puntos en los que se anula la derivada).
- Nota: si la función no es derivable en algún punto del dominio, tendremos que comprobar si dicho punto es un extremo.
- Monotonía
- Estudiamos el signo de la derivada en algún punto de los intervalos en que los puntos críticos dividen el dominio:
- Si el signo es positivo: la función crece en el intervalo al que pertenece el punto.
- Si el signo es negativo: la función decrece.
- Según la monotonía, sabemos si los puntos críticos son extremos y, en tal caso, si son máximos o mínimos:
- Si es creciente a la izquierda del punto crítico y decreciente a la derecha, se trata de un máximo.
- Si es decreciente a la izquierda del punto crítico y creciente a la derecha, se trata de un mínimo.
- Si es creciente o decreciente a la derecha e izquierda del punto crítico, no es un extremo.
- Nota: para saber si un máximo (mínimo) es absoluto, hay que comprobar que no hay puntos del dominio para los cuales la función tenga un valor superior (inferior) que para el máximo (mínimo).
- Nota: si un punto crítico es un máximo, la segunda derivada en dicho punto es negativa. Si es un mínimo, es positiva.
- Convexidad
- Calculamos la segunda derivada.
- Buscamos los puntos de inflexión, posibles cambios de convexidad a concavidad (o viceversa), que son los puntos que anulan la segunda derivada. Los puntos de cambio de definición también pueden ser puntos de inflexión aunque no anulen la segunda derivada.
- La forma más sencilla de comprobar la convexidad, es mediante la gráfica de la función.
- Nota: si la tercera derivada es no nula en un posible punto de inflexión, entonces es un punto de inflexión.
Ejercicios Resueltos
| EJERCICIOS RESUELTOS (click para ver la solución) |
| 1 |
|
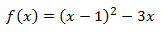
|
| SOLUCIÓN |
|
Dominio:
El dominio es todos los reales ya que la función es polinómica.
Puntos críticos:
Calculamos la primera derivada:
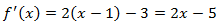
Calculamos los puntos críticos, que son los que anulan la derivada:
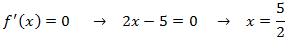
Monotonía:
Estudiamos el signo de la derivada en los dos intervalos en los que el punto crítico
divide el dominio. Para ello es suficiente tomar un punto al azar de cada intervalo.
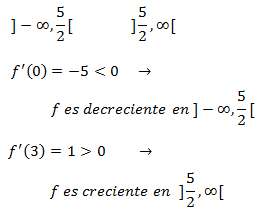
Puesto que la función es decreciente a la izquierda del punto crítico y creciente a su derecha,
deducimos que se trata de un mínimo. Además, es un mínimo absoluto.
Puntos de inflexión: los candidatos son los que anulan la segunda derivada.
La segunda derivada es:
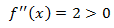
La segunda derivada nunca se anula y, por tanto, no existen puntos de inflexión. De modo que la función
es convexa o cóncava en todo su dominio.
Como se trata de una parábola (polinomio de segundo grado) con coeficiente director positivo, la función
es convexa (también lo podemos deducir del hecho de que su único extremo absoluto es un mínimo).
La gráfica de la función es
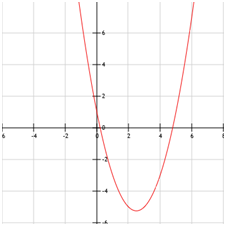
|
|
|
| 2 |
|
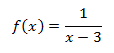
|
| SOLUCIÓN |
|
Dominio:
La función es racional, por lo que el dominio es todos los reales excepto los puntos para los
que se anula el denominador, es decir, todos los reales menos x =3 .
Puntos críticos:
Calculamos la primera derivada:
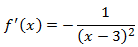
Los puntos críticos son los que anulan la derivada, pero como la función derivada nunca puede valer 0, no
existen puntos críticos y, por tanto, tampoco extremos. Esto se debe a que la derivada se anula siempre en los
extremos y como esto no ocurre, no puede haberlos.
Monotonía:
Al no haber puntos críticos, estudiamos el signo de la derivada en los intervalos del dominio. Notemos
que la derivada es siempre negativa (el denominador es siempre positivo por ser un cuadrado). Así pues, la función
es monótona decreciente en todo su dominio.
Puntos de inflexión: los candidatos son los que anulan la segunda derivada.
La segunda derivada es:
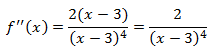
De nuevo ocurre que la función es de signo constante, luego nunca se anula. Tenemos que no hay puntos de inflexión, lo
que quiere decir que la función es convexa o cóncava. Pero notemos que esto es para cada intervalo, es decir,
será siempre convexa o cóncava en un mismo intervalo, pero no tiene que tener la misma forma en ambos intervalos. De hecho,
la función es cóncava en el intervalo de la izquierda y convexa en el otro.
La gráfica de la función es
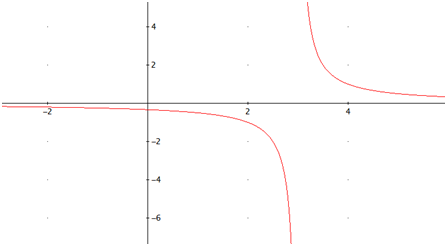
|
|
|
| 3 |
|
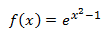
|
| SOLUCIÓN |
|
Dominio:
El dominio es todos los reales: la exponencial ex no tiene problemas de
definición para ningún número real. Por ello, si cambiamos x por x 2 -1
seguimos sin tenerlos.
Puntos críticos:
Calculamos la primera derivada, que consiste en multiplicar por la derivada del exponente, e igualamos a 0
para buscar los puntos críticos:
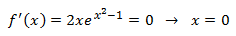
Es decir, el único punto crítico es x = 0.
Monotonía:
En realidad, podemos determinar la monotonía intuitivamente: como sabemos que la exponencial es creciente, al tener en el exponente una parábola (con un mínimo en
x = 0 ), la función tendrá un mínimo en x = 0.
No obstante, lo haremos analíticamente: estudiamos el signo de la derivada en los dos intervalos en los que el punto crítico
divide el dominio. Para ello es suficiente tomar un punto al azar de cada intervalo.
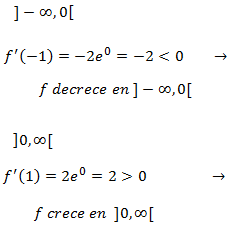
Puesto que la función es decreciente en los negativos y creciente en los positivos, presenta un mínimo en el punto crítico. Además, es un mínimo absoluto.
Puntos de inflexión: los candidatos son los que anulan la segunda derivada. Calculamos la derivada y la igualamos a 0:
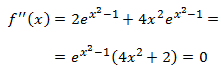
El producto será cero cuando alguno (o los dos) de sus factores sea 0. Pero esto no ocurre porque
uno de ellos es la exponencial (nunca vale 0) y una ecuación de segundo grado sin raíces (reales).
Luego no existen puntos de inflexión y la función es convexa o cóncava en todo su dominio.
De la monotonía (decreciente y creciente con un mínimo) deducimos que la función es convexa en todo su dominio.
La gráfica de la función es
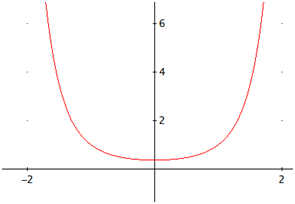
|
|
|
| 4 |
|
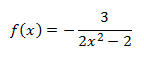
|
| SOLUCIÓN |
|
Dominio:
Como la función es racional, el dominio es todos los reales excepto los puntos para
los que se anula el denominador. Notemos que podemos escribir la función como:
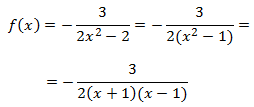
Lo hemos hecho así para seguir siempre el mismo procedimiento: cuando tenemos una funcional
racional tenemos que expresar los polinomios del denominador y numerador de forma factorizada ya que
de este modo podemos simplificar la expresión. La razón de esto es que determinadas raíces del denominador
(punto donde vale 0 el denominador) pueden ser raíces en el numerador.
Por ejemplo, si no simplificamos la función
$$f(x)=\frac{x-1}{x-1}$$
podríamos incurrir en el error de considerar x = 1 como raíz del denominador y, por tanto,
excluirla del dominio, siendo esto un grave error ya que se trata de la funcón constante f(x) = 1.
Luego el dominio de nuestra función es todos los reales exceto x = 1 y x = -1.
Puntos críticos:
Calculamos la primera derivada:
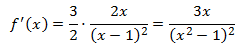
El único punto crítco es x = 0 ya que anula la derivada.
Monotonía:
Tenemos que estudiar el signo de la derivada en los intervalos que genera el punto crítico, pero
tenemos que tener en cuenta los puntos que no forman parte del dominio. Para simplificar los cálculos,
como el denominador siempre es positivo, sólo usaremos el signo del numerador.

Por tanto, el punto crítico es un mínimo. Además, no es un extremo absoluto ya que
cuando el denominador tiende a 0, la función tiene a menos infinito. Luego seguro que
existen puntos de la función con valores menores que para el mínimo.
Puntos de inflexión: los candidatos son los que anulan la segunda derivada, que son
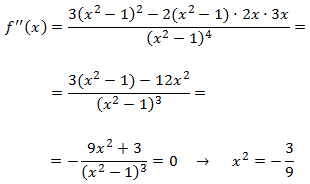
Luego no tenemos puntos de inflexión ya que las soluciones a la ecuación no son reales. Así pues, la función
será convexa o cóncava en cada intervalo.
Para saberlo, debido a que la función es más compleja que en los casos anteriores, miraremos su gráfica.
Para dibujarla, tendremos que calcular los límites laterales en los puntos que no pertenecen al dominio, así como
los límites en los infinitos.
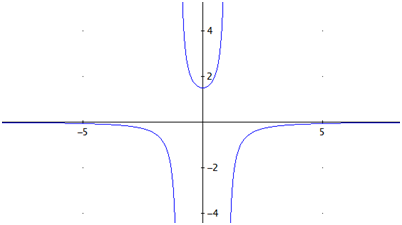
Por tanto, la función es cóncava, convexa y cóncava, respectivamente, en cada intervalo.
|
|
|
| 5 |
|
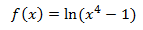
|
| SOLUCIÓN |
|
Dominio:
La función es un logaritmo (sin valor absoluto), por lo que el argumento (lo de dentro) tiene
que ser mayor que 0. Es decir,
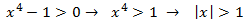
Con lo que el dominio es
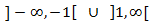
Puntos críticos:
Calculamos la primera derivada e igualamos a 0:
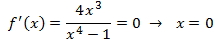
En un principio, tenemos un único punto crítico, x = 0. Pero como este punto no
forma parte del dominio, no puede ser punto crítico.
Como no hay puntos críticos, no puede haber extremos.
Monotonía:
Estudiamos el signo de la derivada en los dos intervalos que conforman el dominio:
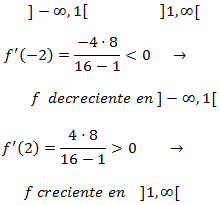
Puntos de inflexión: los candidatos son los que anulan la segunda derivada, que es:
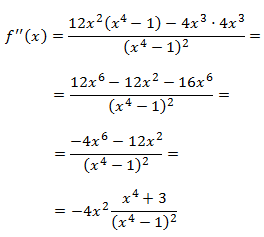
Igualamos 0 y obtenemos:
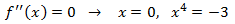
Ninguna de las soluciones forma parte del dominio, así que no hay puntos de inflexión.
Al dibujar la gráfica observamos que la función es cóncava en todo su dominio.
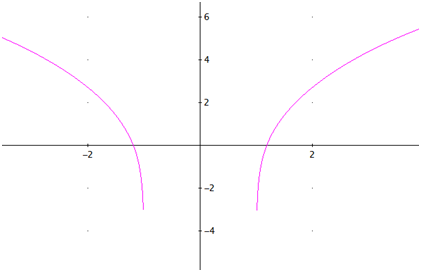
|
|
|
| 6 |
|
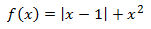
|
| SOLUCIÓN |
|
Dominio:
El dominio es todos los reales ya que la función es polinómica (aunque haya un valor absoluto).
Puntos críticos:
Notemos que podemos escribir la función como una función definida a trozos
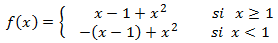
Calculamos la primera derivada, que también será a trozos:
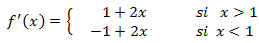
Notemos que la función no es derivable en el punto x = 1 ya que los límites laterales de la derivada
en dicho punto no coinciden. Esto se debe al ángulo que tendremos en la gráfica debido al valor absoluto (al igual que
ocurre en la función f (x) = |x| en 0).
Calculamos los puntos críticos, que son los que anulan la derivada:
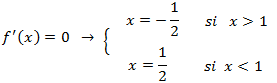
Tenemos que tener en cuenta que el primer punto (x = - 1/2) no es punto crítico ya que no pertenece
al intervalo de definición.
Monotonía:
Estudiamos el signo de la derivada en los intervalos que proporciona el punto crítico, pero también el punto para el cuál la función no es derivable:
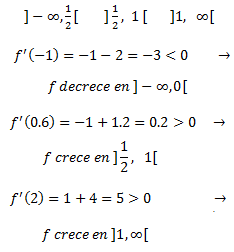
Puesto que la función es decreciente a la izquierda del punto crítico y creciente a su derecha,
deducimos que se trata de un mínimo. Además, es un mínimo absoluto.
Puntos de inflexión: los candidatos son los que anulan la segunda derivada. No hay
ya que ésta es
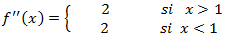
La segunda derivada nunca se anula y, por tanto, no existen puntos de inflexión. De modo que la función
es convexa o cóncava en todo su dominio.
La función es convexa.
La gráfica de la función es
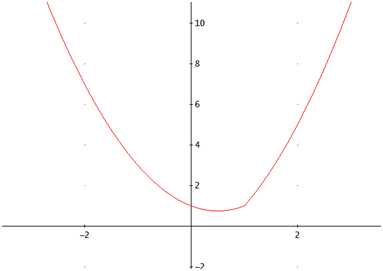
|
|
|
| 7 |
|
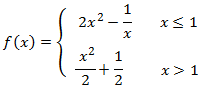
|
| SOLUCIÓN |
|
Dominio:
Se trata de una función definida a trozos. En uno de ellos tenemos un denominador que se anula en
x = 0. Así que el dominio es todos los reales excepto dicho punto.
Puntos críticos:
Calculamos la primera derivada:
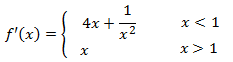
Igualamos a 0:
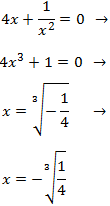
Notemos que x = 0 no es un punto crítico.
Monotonía:
Estudiamos el signo de la derivada en los dos intervalos en los que el punto crítico
divide el dominio. Además, también tenemos que incluir la paritición que genera el punto x = 1
ya que es donde cambia la definición de la función. De hecho, en este último punto la función no es
derivable ya que no coinciden los límites laterales
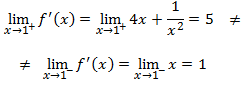
Estudiamos el signo:
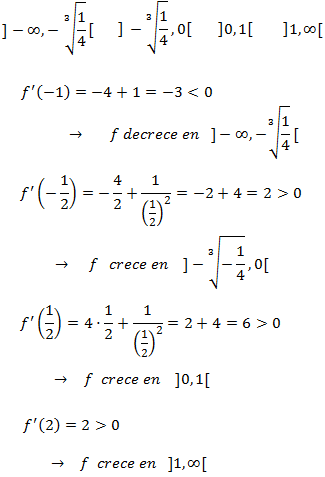
Por tanto, el punto crítico es un mínimo.
Puntos de inflexión: los candidatos son los que anulan la segunda derivada
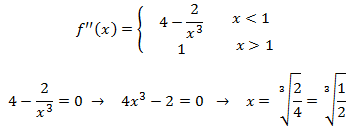
Tenemos un posible punto de inflexión. Como el cálculo de la tercera derivada es sencillo, la usaremos
para saber si en efecto es un punto de inflexión:
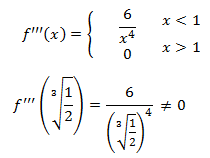
Como la tercera derivada no se anula en dicho punto, sí es un punto de inflexión.
La gráfica de la función es
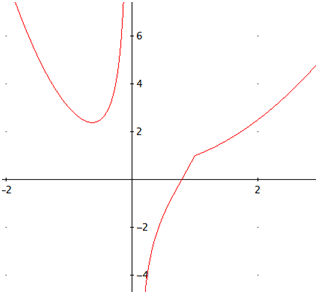
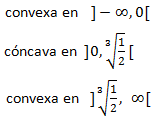
|
|
|
| EJERCICIOS RESUELTOS (click para ver la solución) |
| 8 |
|
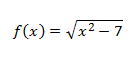
|
| SOLUCIÓN |
|
Dominio:
La función es una raíz cuadrada, así que el dominio es los reales que hacen que el radicando
sea no negativo.
Ha de cumplirse:
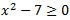
Resolviendo la ecuación de segundo grado asociada a la desigualdad, obtenemos que el dominio es
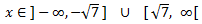
Puntos críticos:
Calculamos la primera derivada:
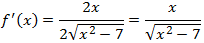
Igualamos a 0:
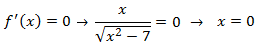
Obtenemos el valor x = 0, pero no se trata de un punto crítico ya que no forma parte del dominio.
Monotonía:
Estudiamos el signo de la derivada en los dos intervalos que conforman el
dominio de la función:
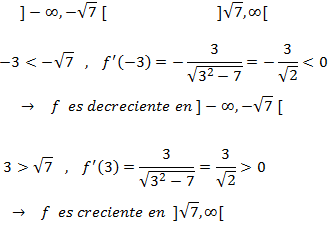
No tenemos puntos críticos, pero notemos que
$$x =\pm \sqrt{7}$$
son los puntos de los extremos de los intervalos del dominio, que se incluyen ya que en ellos
la función toma un valor determinado (no como en el caso de los infinitos).
Por la monotonía, estos puntos son dos mínimos de la función. Además, son dos extremos absolutos ya que
$$f(\pm \sqrt{7}) = 0 \leq f(x) \ \forall x \in \ dominio$$
Puntos de inflexión: los candidatos son los que anulan la segunda derivada, que es:
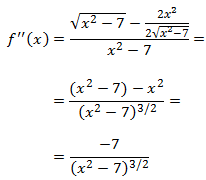
La segunda derivada nunca se anula y, por tanto, no existen puntos de inflexión. De modo que la función
es convexa o cóncava en cada intervalo: cóncava en el primero y convexa en el segundo.
La gráfica de la función es
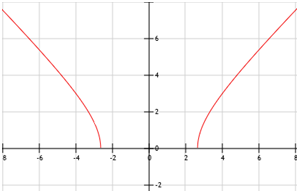
|
|
|
| 9 |
|
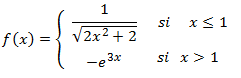
|
| SOLUCIÓN |
|
Dominio:
La función está definida a trozos. Cuando x > 1, no tenemos ningún problema en la definición.
En el
otro caso, tenemos una raíz en el denominador, así que tenemos que excluir del dominio los puntos que hacen que
el radicando sea 0 ó negativo. Pero las raíces de la ecuación de segundo grado no son reales y el radicando siempre
es mayor que 0.
Por tanto, el dominio es todos los reales.
Notemos que la función no es continua en x = 1 ya que los límites laterales en dicho punto
no coinciden (la exponencial y la fracción no pueden valer lo mismo).
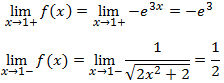
Puntos críticos:
Calculamos la primera derivada:
Para facilitar el cálculo, escribiremos
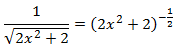
Así, tenemos
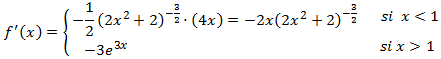
Igualamos a 0:
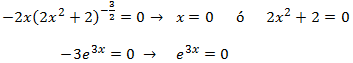
El único punto crítico es x = 0.
Monotonía:
Estudiamos el signo de la derivada en los tres intervalos en los que el punto crítico divide al dominio:
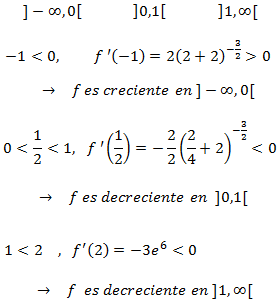
Tenemos un máximo (absoluto) en x = 0 y un máximo (relativo) en x = 1 (es un extremo del dominio).
Puntos de inflexión: los candidatos son los que anulan la segunda derivada, que es:
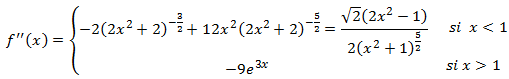
Igualamos a 0:
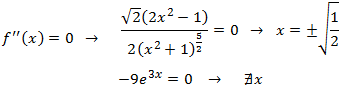
Como tenemos dos candidatos, usaremos el criterio de la tercera derivada:
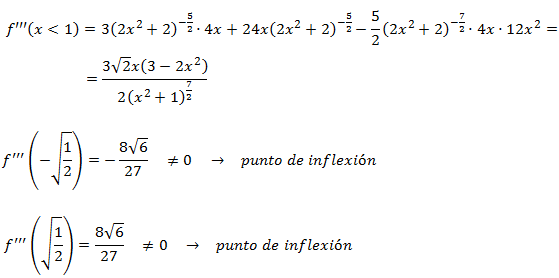
Tenemos dos puntos de inflexión. La función es
convexa, cóncava, convexa y cóncava, respectivamente, en los intervalos
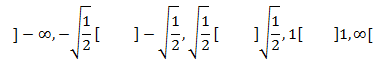
La gráfica de la función es, a distintas escalas
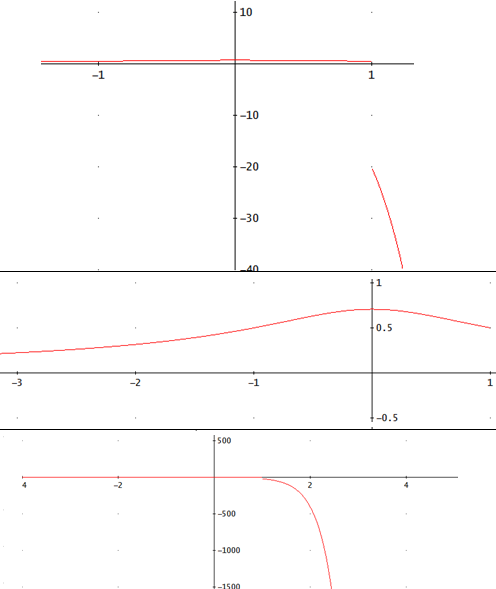
|
|
|
| 10 |
|
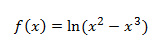
|
| SOLUCIÓN |
|
Dominio:
Como tenemos un logaritmo, necesitamos que el argumento (lo de dentro) sea mayor que cero.
Debemos excluir los demás puntos del dominio. Es decir, queremos
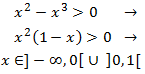
Puntos críticos:
Calculamos la primera derivada y la igualamos a 0:
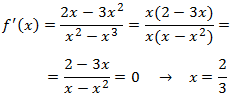
Por tanto, sólo hay un punto crítico.
Monotonía:
Estudiamos el signo de la derivada en los intervalos del dominio, añadiendo la partición que genera
el punto crítico obtenido.
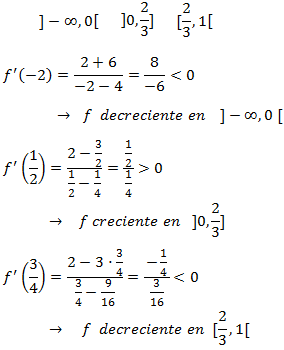
Tenemos un máximo en 2/3. Notemos que los otros extremos de los intervalos no son extremos de la función ya que no pertenecen al dominio.
Puntos de inflexión: los candidatos son los que anulan la segunda derivada:
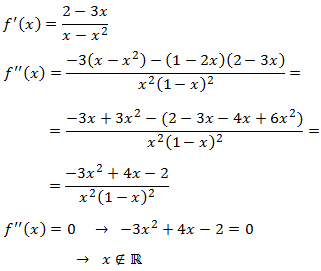
No existen puntos de inflexión ya que al igualar a 0 la segunda derivada obtenemos una
ecuación de segundo grado que no tiene soluciones reales. Por consiguiente, la función será
o bien cóncava o bien convexa en cada intervalo de su dominio, es decir, sin haber cambios en un mismo intervalo.
La gráfica de la función es
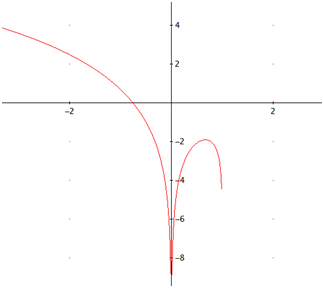
La función es cóncava en los dos intervalos de su dominio.
|
|
|
| 11 |
|
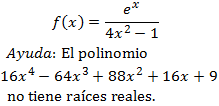
|
| SOLUCIÓN |
|
Dominio:
Como es una función racional, tenemos que evitar los ceros en el denominador:
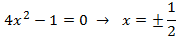
Por tanto, el dominio es
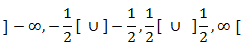
Puntos críticos:
Calculamos la primera derivada e igualamos a 0:
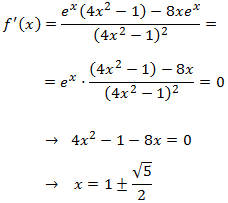
Hay dos puntos críticos.
Monotonía:
Estudiamos el signo de la derivada en los intervalos en los que los puntos críticos dividen el
dominio:
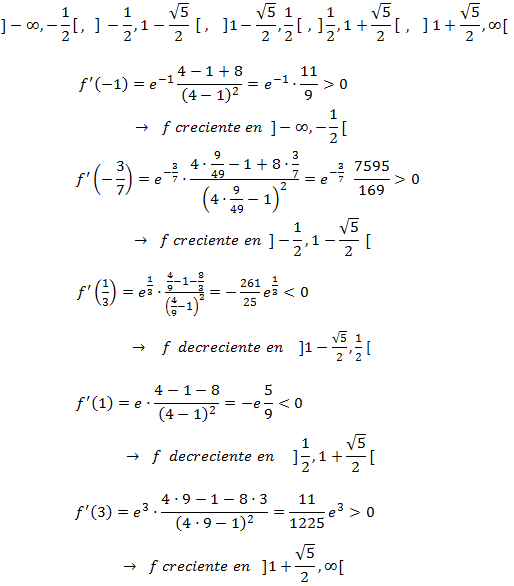
Por tanto, los puntos críticos
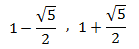
son un máximo y un mínimo respectivamente.
Puntos de inflexión: los candidatos son los que anulan la segunda derivada
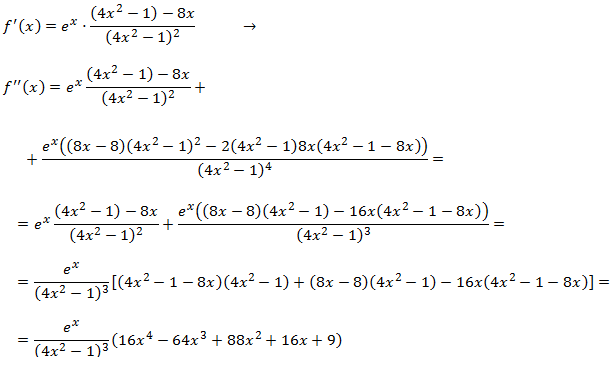
Como el polinomio no tiene raíces reales, no hay ningún punto de inflexión.
La gráfica de la función es
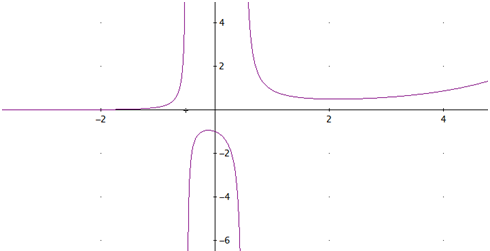
Convexa, cóncava y convexa, respectivamente, en cada intervalo del dominio.
|
|
|
| 12 |
|
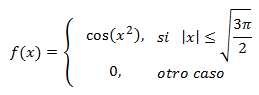
|
| SOLUCIÓN |
|
Dominio:
La función está definida por partes. En un intervalo es una función trigonométrica (coseno) que
no tiene ningún problema de definición y, en la otra, una función constante. Por tanto, el dominio
es todos los reales.
Puntos críticos:
Calculamos la derivada que también es una función definida a trozos:
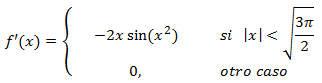
Notemos que la desigualdad es estricta porque en dichos puntos la función no es derivable (no existe la derivada)
ya que los límites laterales no coinciden
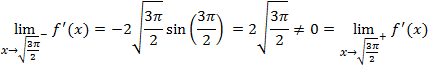
(análogo para el otro punto)
Tendremos que considerar estos dos puntos como posibles extremos.
Igualamos a cero:
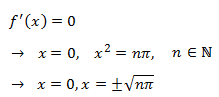
Notemos que obtenemos infinitos puntos críticos: en el intervalo donde la función es constante la derivada
siempre es 0, pero por esto mismo, sabemos que no se tratan de extremos; en el otro intervalo, obtenemos los
puntos críticos de la forma
$$ \pm \sqrt{n\pi} = \pm \sqrt{\pi}, \ \pm \sqrt{2\pi}, \ \pm \sqrt{3\pi}... $$
Pero los únicos que forman parte del intervalos en dicho intervalo son solamente
$$0, \ \pm \sqrt{\pi}$$
ya que
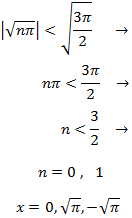
Monotonía:
Estudiamos el signo de la derivada en los intervalos en los que los puntos críticos dividen el
dominio, excepto en el primero y en el último donde ya sabemos que es constante:
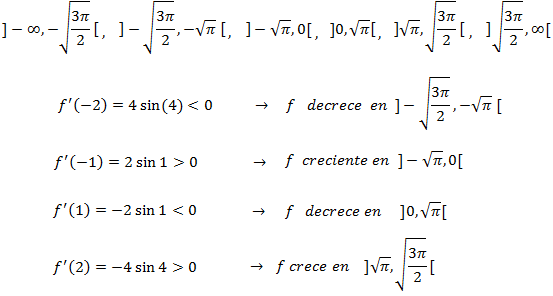
Por tanto, los puntos críticos
$$ -\sqrt{\pi}, 0, \ \sqrt{\pi}$$
son un mínimo, un máximo y un mínimo respectivamente. Además, son extremos absolutos.
Puntos de inflexión: los candidatos son los que anulan la segunda derivada
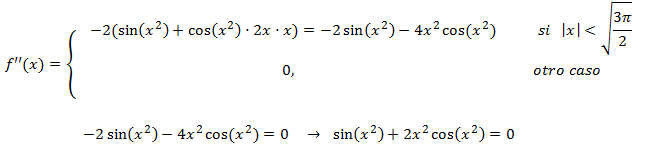
Encontrar los puntos de inflexión analíticamente no es fácil. Es más sencillo hacerlo observando
su gráfica, que es sencilla por tratarse de un coseno y una función constante:
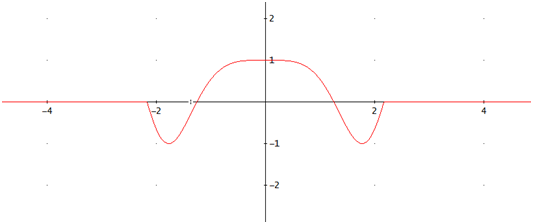
Vemos que hay dos puntos de inflexión en los puntos, aproximados,
$$\pm \frac{\sqrt{\pi}}{4}$$
La función es convexa, cóncava y convexa.
|
|
|


Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.