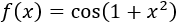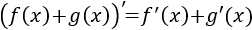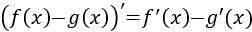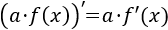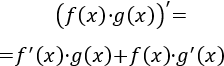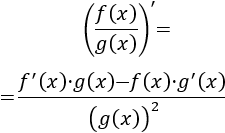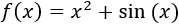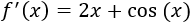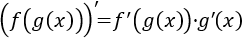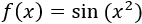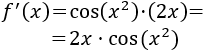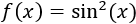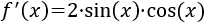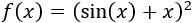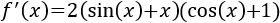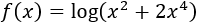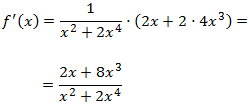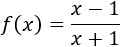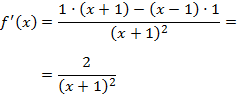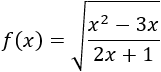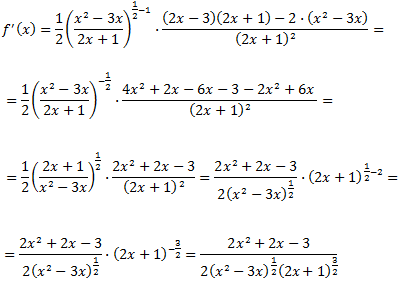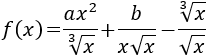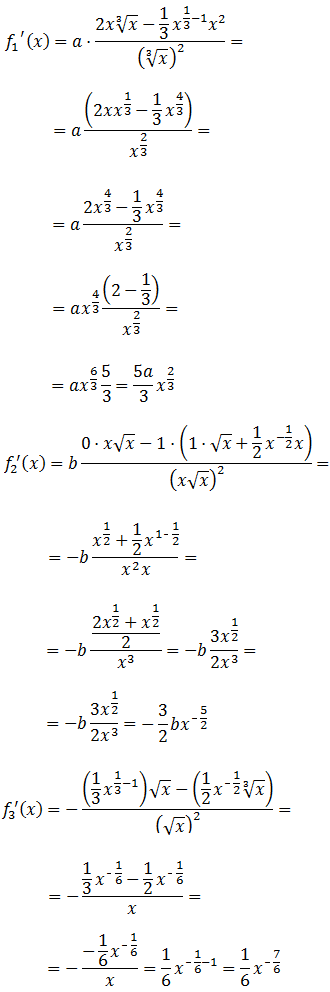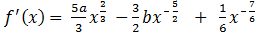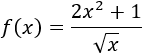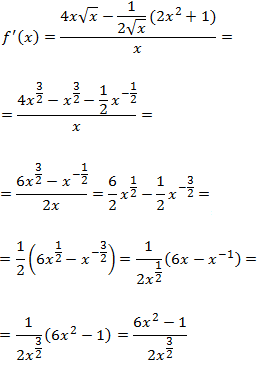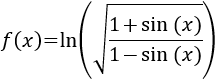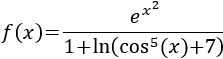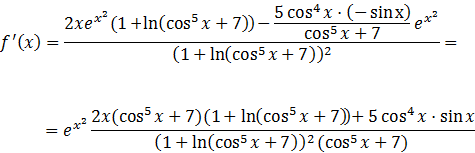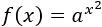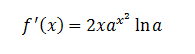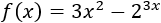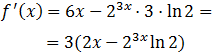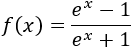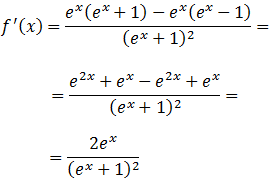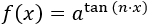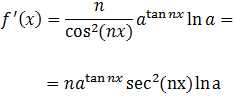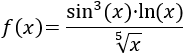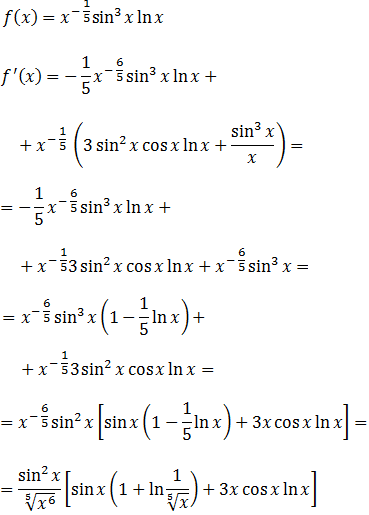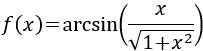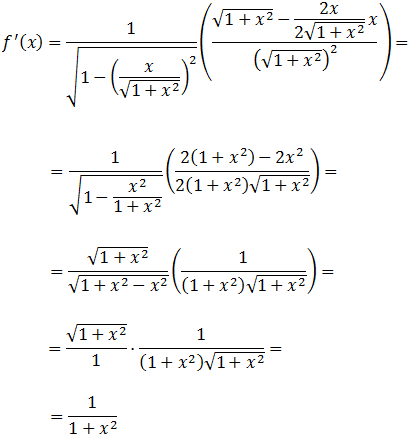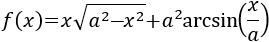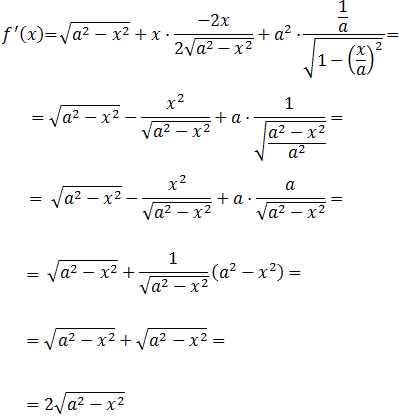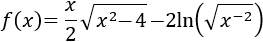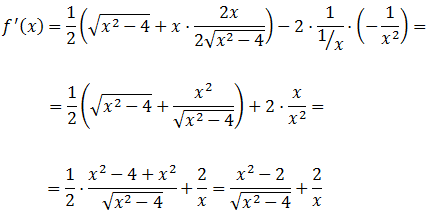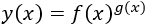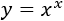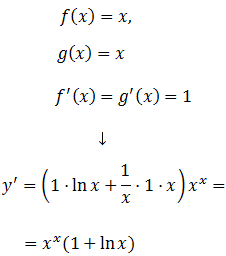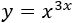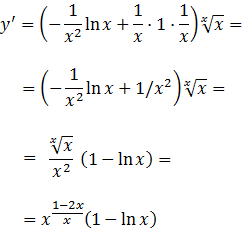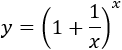Ejercicio 1
Función logarítmica:
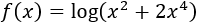
Solución
Derivamos el logaritmo y multiplicamos por la derivada del argumento, que es un polinomio:
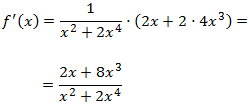
Simplificando,
$$ f'(x) = \frac{2(1+4x^2)}{x(1+2x^2)} $$
Ejercicio 2
Función racional:
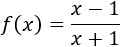
Solución
Aplicamos la regla del cociente:
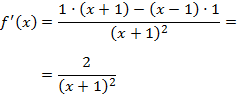
Ejercicio 3
Función con raíz cuadrada:
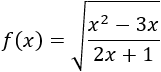
Solución
Podemos escribir la raíz cuadrada como una potencia (de exponente 1/2) para derivar la raíz como una potencia:
$$ f(x) = \left(\frac{x^2-3x}{2x+1}\right)^\frac{1}{2}$$
Calculamos la derivada:
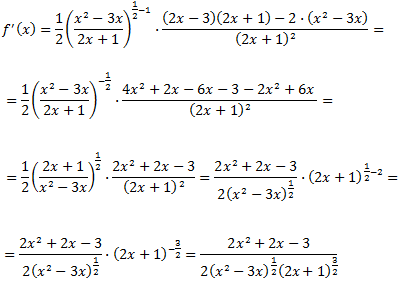
Ejercicio 4
Función con raíces de distintos órdenes y parámetros:
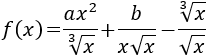
Solución
Como la función es una suma, su derivada es la suma de las derivadas.
Para abreviar, caluclamos las derivadas de cada sumando por separado.
Sean
las funciones
$$ f_1(x)= \frac{ax^2}{\sqrt[3]{x}} $$
$$ f_2(x)= \frac{b}{x\sqrt{x}} $$
$$ f_3(x) =\frac{\sqrt[3]{x}}{\sqrt{x}} $$
Las derivadas son:
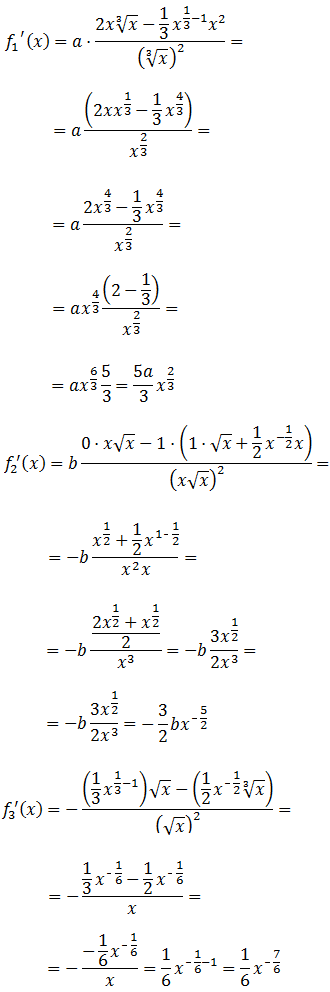
Luego la derivada de la función es
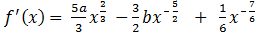
Ejercicio 5
Función con raíz en el denominador:
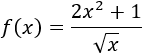
Solución
Derivamos el cociente:
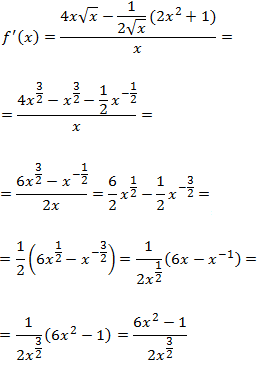
Ejercicio 6
Función logarítmica con cociente de raíces:
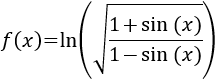
Solución
Antes de aplicar la regla de la cadena, podemos aplicar las propiedades
de los logaritmos para evitar la raíz.
La función queda como:
$$ f(x)= \frac{1}{2}ln\left( \frac{1+sin(x)}{1-sin(x)} \right)$$
Aplicando de nuevo las propiedades, podemos evitar la fracción:
$$ f(x) = \frac{1}{2}ln\left( 1+sin(x)\right)-\frac{1}{2}ln\left( 1-sin(x)\right) $$
Calculamos la derivada:
$$ f'(x) = \frac{1}{2}\cdot \frac{cos(x)}{1+sin(x)}-\frac{1}{2}\cdot \frac{-cos(x)}{1-sin(x)}$$
Operamos para simplificar la expresión (sumando las fracciones):
$$f'(x)= \frac{1}{2}\left( \frac{cos(x)-cos(x)sin(x)+cos(x)+cos(x)sin(x)}{(1+sin(x))(1-sin(x))} \right) $$
$$ = \frac{1}{2}\left( \frac{2cos(x)}{(1+sin(x))(1-sin(x))}\right) $$
En el denominador tenemos una suma por diferencia:
$$ f'(x)= \frac{1}{2}\left( \frac{2cos(x)}{1-sin^2(x)}\right) $$
Finalmente, simplificamos la fracción aplicando la fórmula fundamental
de trigonometría ( \(cos^2(x)+sin^2(x) = 1\) ):
$$ f'(x)= \frac{1}{2}\left( \frac{2cos(x)}{cos^2(x)}\right) =$$
$$ = \frac{1}{2}\left( \frac{2}{cos(x)}\right) = \frac{1}{cos(x)}$$
Ejercicio 7
Función con logaritmo natural en el denominador:
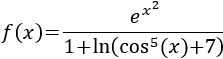
Solución
Tenemos que aplicar la regla del cociente. Observad que el exponente del numerador está al cuadrado.
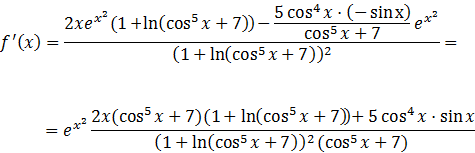
Ejercicio 8
Función exponencial:
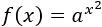
Solución
Recordamos que la derivada de una exponencial es la derivada del
exponente multiplicada por el logaritmo de la base y por la propia función:
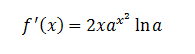
Ejercicio 9
Función exponencal:
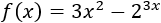
Solución
Tenemos de nuevo una exponencial con base distinta de e.
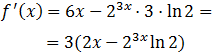
Ejercicio 10
Función cociente con exponenciales:
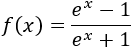
Solución
Ejercicio 11
Función exponencial con tangente:
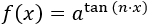
Recordad que \(sec(x) = 1/cos(x)\).
Solución
Se trata de una exponencial cuya base es un parámetro, a, por lo que en su
derivada tendremos el factor ln(a). Además, en el exponente tenemos una función trigonométrica con otro parámetro, n.
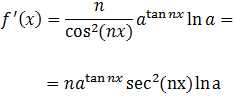
Ejercicio 12
Función cociente con seno, logaritmo y raíz quinta:
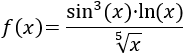
Solución
Hay que tener en cuenta que la raíz no es cuadrada (es de orden 5).
Podemos considerarla como una potencia de exponente 1/5.
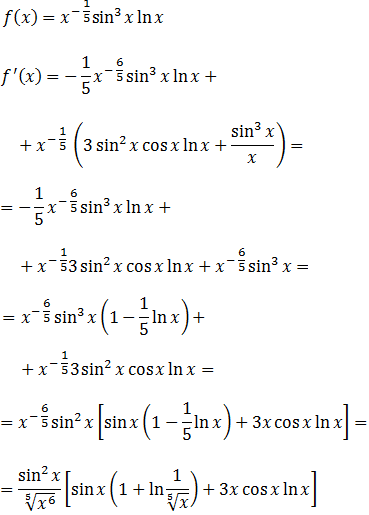
Ejercicio 13
Función arcocoseno:
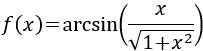
Solución
La dificultad de esta derivada es conocer la derivada de arcsin(x).
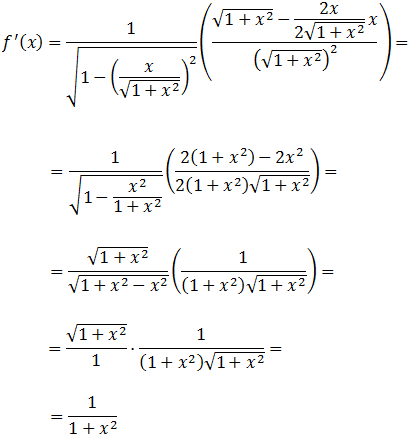
Ejercicio 14
Función con raíz, arcocoseno y parámetro:
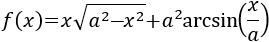
Solución
Ejercicio 15
Función con raíces y logaritmo:
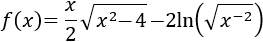
Solución
Ejercicio 16
Demostración de la derivada de una función elevada a una función:
Solución
Vamos a calcular la derivada de una función elevada a otra función.
Para simplificar, llamaremos \( y=f(x)\), \(f =f(x)\) y \(g=g(x)\), y a sus derivadas, \(y'=y'(x)\), \( f'=f'(x)\) y \(g'=g'(x)\).
Por tanto, queremos calcular la derivada de
$$ y = f^g $$
Aplicamos logaritmos y sus propiedades a la igualdad anterior:
$$ ln(y) = ln(f^g) $$
$$ ln(y) = g\cdot ln(f) $$
Derivamos en la igualdad (derivada del producto y del logaritmo) aplicando
la regla de la cadena:
$$ \frac{y'}{y} = g'\cdot ln(f) + g\cdot \frac{f'}{f} $$
Aislamos \( y'\) en la expresión anterior:
$$ y' = y\cdot \left(g'\cdot ln(f) + g\cdot \frac{f'}{f} \right)$$
Por tanto, hemos obtenido una fórmula para calcular \(y'\) en términos de
\(y\) y las funciones \(f\) y \(g\) y sus derivadas.
Ejercicio 17
Función exponencial:
Solución
Para calcular la derivada de esta función, no podemos aplicar
directamente las fórmulas de la derivada de la exponencial
ni de la derivada de una potencia. Sí podemos aplicar la fórmula calculada
en el Ejercicio 16.
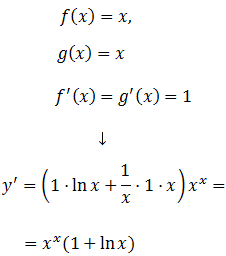
Ejercicio 18
Función exponencial:
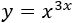
Solución
De nuevo, tenemos que emplear la fórmula del Ejercicio 16:
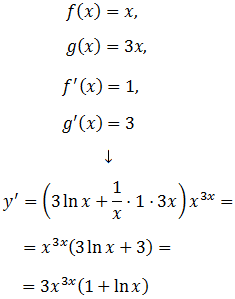
Ejercicio 19
Función con raíz \(x-\)ésima:
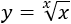
Solución
Aplicamos la fórmula del Eejercicio 16:
Sean las funciones \(f(x) = x\), \(g(x)=\frac{1}{x}\) e
\( y = f(x)^{g(x)}\). Las derivadas son:
$$ f'=1,\ g'=-\frac{1}{x^2} $$
Por tanto,
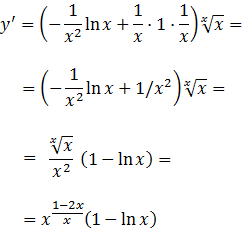
Ejercicio 20
Función exponencial:
Solución
Aplicamos la fórmula del Ejercicio 16:
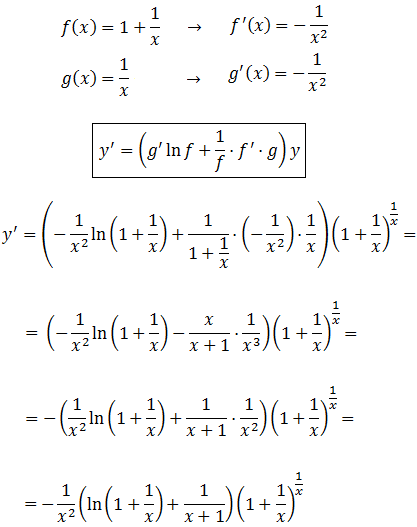


Cálculo de derivadas (regla de la cadena) - © matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.