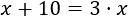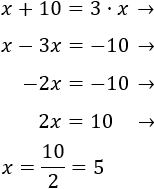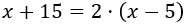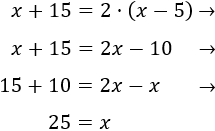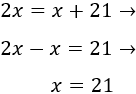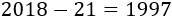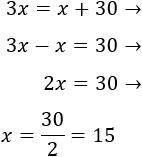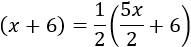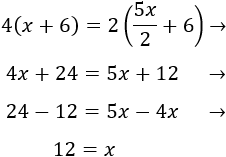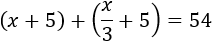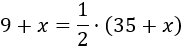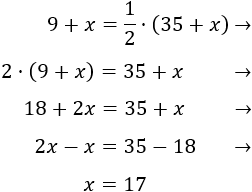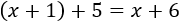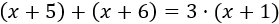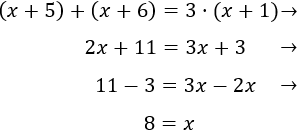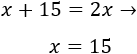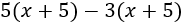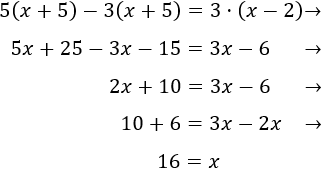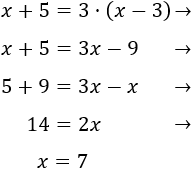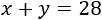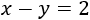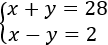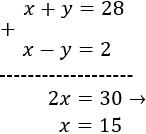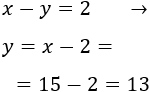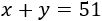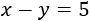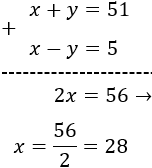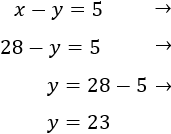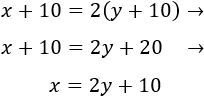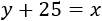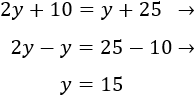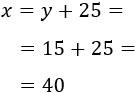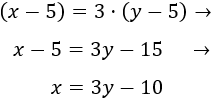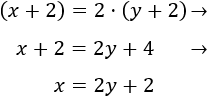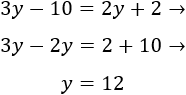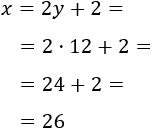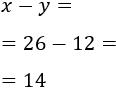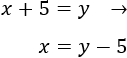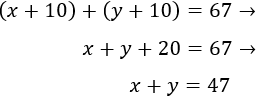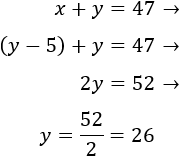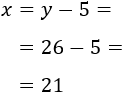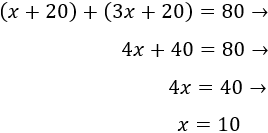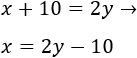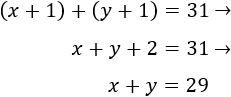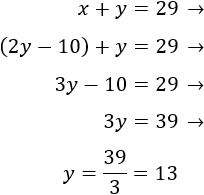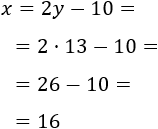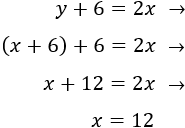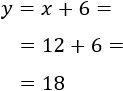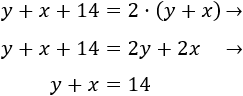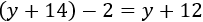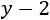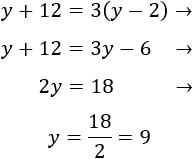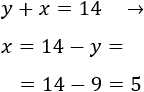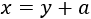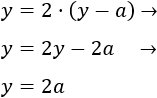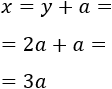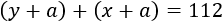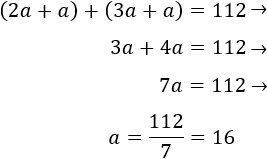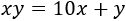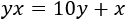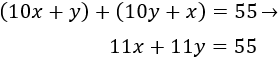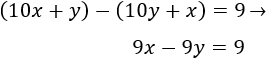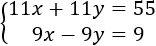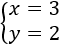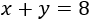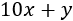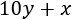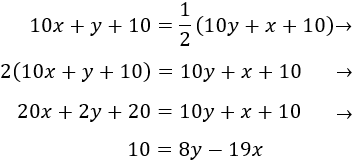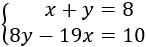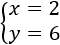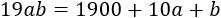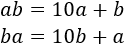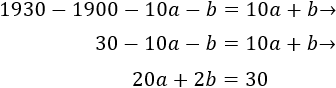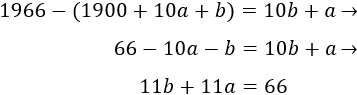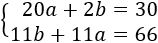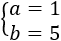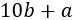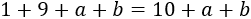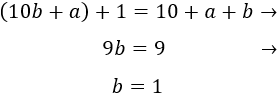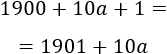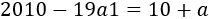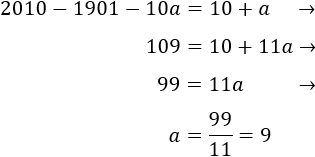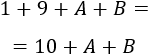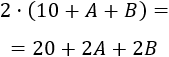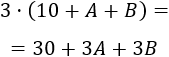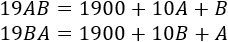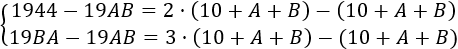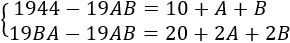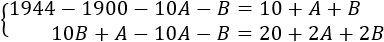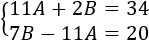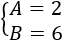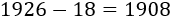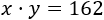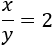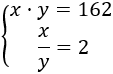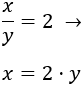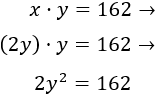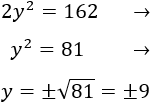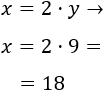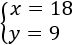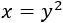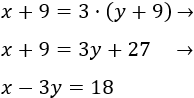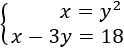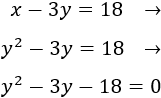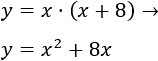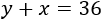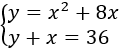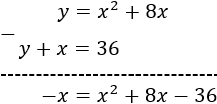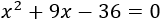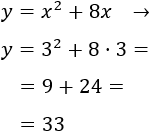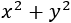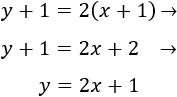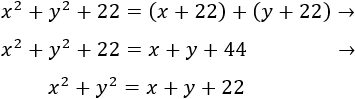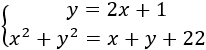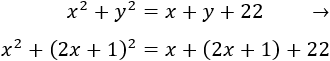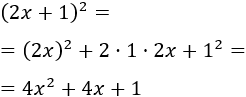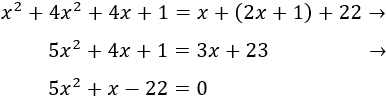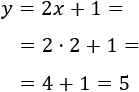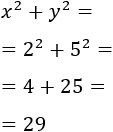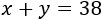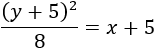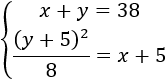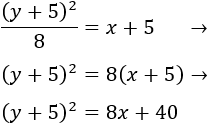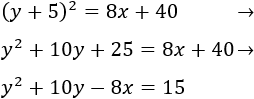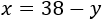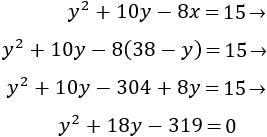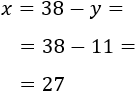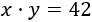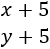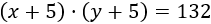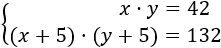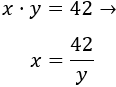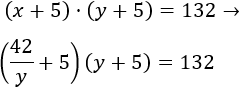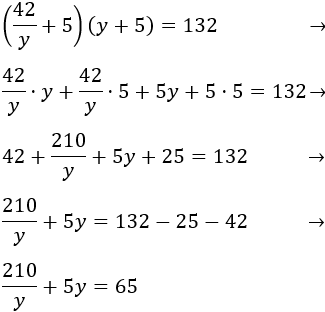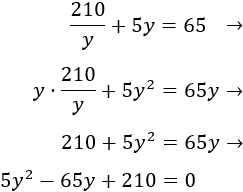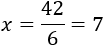Problemas para resolver con una ecuación
Problema 1 
Si dentro de 10 años Adriana tiene el triple de la edad que tiene ahora, ¿qué edad tendrá entonces?
SOLUCIÓN:
Llamamos \(x\) a la edad actual de Adriana. Entonces,
-
\(x\) son los años que tiene Adriana ahora;
-
\(3\cdot x\) es el triple de la edad actual de Adriana;
-
\(x + 10\) son los años que tendrá Adriana dentro de 10 años (al pasar 10 años, sumamos 10 a su edad).
La ecuación que expresa que dentro de 10 años la edad de Adriana será el triple que la actual es
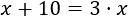
Resolvemos la ecuación de primer grado:
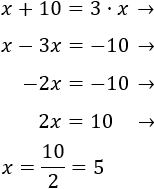
Luego la edad actual de Adriana es 5 años.
Dentro de 10 años, su edad será 15, que es el triple de su edad actual ya que \(3\cdot 5 = 15\).
Problema 2 
Si dentro de 15 años Eduardo tiene el doble de edad que la que tenía hace 5 años, ¿qué edad tiene ahora?
SOLUCIÓN:
Llamamos \(x\) a la edad actual de Eduardo. Entonces,
-
\(x\) son los años que tiene Eduardo ahora;
-
\(x-5\) es la edad que tenía Eduardo hace 5 años (como tenía 5 años menos que ahora, le restamos 5 a \(x\));
-
\(2\cdot (x-5)\) es el doble de la edad que tenía Eduardo hace 5 años;
-
\(x + 15\) es la edad de Eduardo dentro de 15 años.
Queremos que dentro de 15 años la edad de Eduardo sea el doble de la que tenía hace 5 años, así que
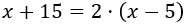
Resolvemos la ecuación:
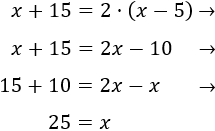
Por tanto, la edad actual de Eduardo es 25.
Comprobamos el resultado: dentro de 15 años, su edad es 40 años, que es el doble de la edad que tenía hace 5 años (entonces tenía 20 años).
Nota: observad que es muy importante el paréntesis cuando escribimos el doble de la edad 15 años atrás ya que no es lo mismo escribir \(2\cdot(x-15)\) que \(2x - 15\).
Problema 3 
Calcular el año de nacimiento de Yolanda sabiendo que en 2039 su edad será el doble que en 2018.
Ayuda: no hay que usar el año actual para el cálculo de la edad.
SOLUCIÓN:
Llamamos \(x\) a la edad de Yolanda en el año 2018.
Entonces, en el año 2039 su edad será \(2\cdot x\), porque así nos lo dice el enunciado del problema.
Ahora bien, del 2039 al 2018 hay 21 años de diferencia, así que la edad de Yolanda en 2039 será la edad de 2018 más 21. Es decir, tenemos la ecuación
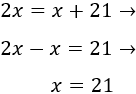
Luego tenemos que la edad de Yolanda en 2018 es 21.
Para calcular su año de nacimiento solo tenemos que restar:
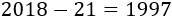
Por tanto, Yolanda nació en el año 1997.
Comprobamos el resultado: su edad en 2018 era 21 y su edad en 2039 será 42 (el doble que en 2018).
Problema 4 
Calcular el año de nacimiento de Ricardo sabiendo que en el año 2003 su edad era el triple que la que tenía en el año 1973.
SOLUCIÓN:
Este problema se resuelve del mismo modo que el anterior.
Si la edad de Ricardo en 1973 era \(x\), su edad en 2003 era \(3x\), porque así lo dice el enunciado del problema.
Como del año 1973 al 2003 hay 30 años de diferencia, la edad de Ricardo en 2003 es la edad que tenía en 1973 más 30:
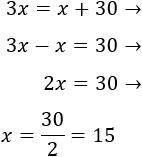
Tenemos que en 1973, la edad de Ricardo era 15. Luego su año de nacimiento es 1973 - 15 = 1958.
Comprobamos el resultado: su edad en 1973 era 15 y su edad en 2003 era 45 (el triple que en 1973).
Problema 5 
La abuela de Lucía tiene 5 veces su edad y su madre tiene la mitad de edad que su abuela. Dentro de 6 años, la edad de Lucía es la mitad que la de su madre, ¿qué edad tiene cada una?
SOLUCIÓN:
Llamamos \(x\) a la edad actual de Lucía. Entonces,
- \(x+6\) es la edad de Lucía dentro de 6 años;
- \(5\cdot x\) es la edad actual de su abuela y dentro de 6 años su edad será \(5\cdot x +6\);
- \(5\cdot x/2\) es la edad actual de su madre y dentro de 6 años será \(5\cdot x/2 + 6\).
Dentro de 6 años, la edad de Lucía es la mitad que la de su madre:
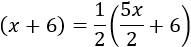
Podemos multiplicar por 4 toda la ecuación para evitar los denominadores antes de resolverla:
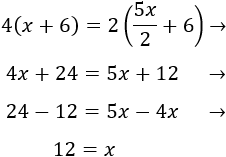
Lucía tiene x = 12 años, su abuela tiene 5x = 60 años y su madre tiene 5x/2 = 30 años.
Comprobamos el resultado: dentro de 6 años, Lucía tendrá 18 años, su abuela 66 y su madre 36. Observad que entonces la edad de Lucía será la mitad que la de su madre (36/2 = 18).
Problema 6 
En el año 2010, la edad de Estefanía era la tercera parte de la edad de su madre y en 2015, sus edades sumaban 54. ¿Qué edad tenía Estefanía en 2010?
SOLUCIÓN:
Llamamos \(x\) a la edad de la madre en el año 2010. En dicho año, la edad de Estefanía era la tercera parte, es decir, \(x/3\).
Cinco años después (en 2015), la edad de Estefanía y la de su madre habían aumentado en 5 unidades. Por tanto, la edad de la madre en 2015 era \(x+5\) y la de Estefanía era \(x/3+5\).
En 2015, la suma de las edades era 54, así que
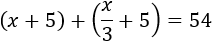
Resolvemos la ecuación:

La edad de la madre en 2010 era x = 33 años y la de Estefanía era x/3 = 11 años.
Problema 7 
Actualmente, la edad de Manuel es 9 años y la de su padre es 35. Calcular cuántos años tienen que pasar para que la edad de Manuel sea la mitad que la de su padre.
SOLUCIÓN:
La incógnita \(x\) es el número de años que tienen que pasar.
Después de \(x\) años, la edad de Manuel es \(9+x\) y la de su padre es \(35+x\). Para entonces debe cumplirse que la edad de Manuel sea la mitad que la de su padre:
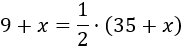
Resolvemos la ecuación:
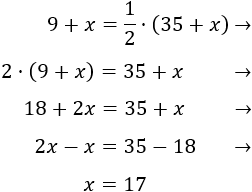
Tienen que pasar 17 años.
Comprobamos el resultado: dentro de 17 años, Manuel tendrá 26 años y su padre tendrá 52 (la edad de Manuel es la mitad que la de su padre: 52/2 = 26).
Problema 8 
Martín es un año mayor que Teresa y dentro de 5 años, la suma de sus edades será el triple que la edad actual de Martín. ¿Qué edad tiene cada uno de ellos?
SOLUCIÓN:
Si \(x\) es la edad de Teresa, la de Martín es \(x+1\). Dentro de 5 años, la edad de ella es \(x+5\) y la de él es
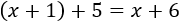
Como la suma de sus edades (dentro de 5 años) es el triple que la edad actual de Martín,
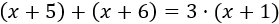
Resolvemos la ecuación:
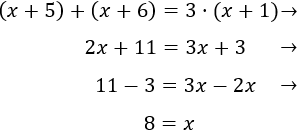
La edad de Martín es 9 y la de Teresa es 8.
Comprobamos el resultado: dentro de 5 años, la edad de Martín es 14 y la de Teresa es 13. La suma de sus edades será 14+13 = 27, que es el triple de la edad actual de Martín (3·9 = 27).
Problema 9 
Si en el año 2009 la edad de María era el doble que la edad que tenía en 1994, ¿en qué año su edad será igual a la suma de su edad en los años 1994 y 2009?
SOLUCIÓN:
Si \(x\) es la edad que tenía María en 1994, en 2009 su edad era \(x+15\) porque habían pasado 15 años.
Como en 2009 la edad de María era el doble de su edad en 1994, tenemos
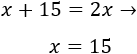
Por tanto, la edad de María en 1994 era 15 y en 2009 era 30. La suma de estas edades es 45. María tendrá 45 años en el año 2024.
Problema 10 
La resta del quíntuple y del triple de la edad de Verónica dentro de 5 años es el triple de la edad que tenía hace 2 años. ¿Qué edad tendrá Verónica dentro de 10 años?
SOLUCIÓN:
Si la incógnita \(x\) es la edad actual de Verónica, dentro de 5 años su edad es \(x+5\). Para entonces, el quíntuple de su edad será \(5(x+5)\) y su triple será \(3(x+5)\). La diferencia de éstos es
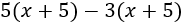
La edad de Verónica hace 2 años era \(x-2\), así que la ecuación del problema es
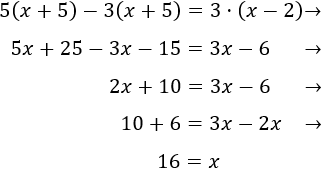
Como la edad actual de Verónica es 16, dentro de 10 años tendrá 26 años.
Problema 11 
Si dentro de 5 años la edad de Jesús será el triple que la que tenía hace 3 años, ¿qué edad tendrá dentro de 10 años?
SOLUCIÓN:
Si \(x\) representa la edad actual de Jesús, dentro de 5 años su edad será \(x+5\) y hace 3 años era \(x-3\).
Resolvemos la ecuación del problema:
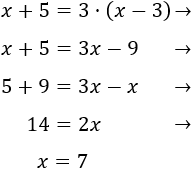
Luego Jesús tiene 7 años y dentro de 10 años tendrá 17.
Problemas para resolver con sistema de ecuaciones lineales
Resolveremos los sistemas por alguno de los tres métodos básicos (sustitución, igualación y reducción).
Problema 12 
La suma de las edades de dos hermanos es 28 y la resta de sus edades es 2. ¿Qué edades tienen los hermanos?
SOLUCIÓN:
Si \(x\) e \(y\) son las edades actuales de los hermanos, su suma es
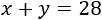
Y la resta de sus edades es
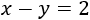
Luego el sistema de ecuaciones del problema es
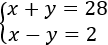
Lo resolvemos por reducción sumando las ecuaciones:
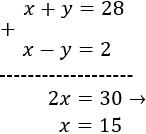
Calculamos la otra incógnita:
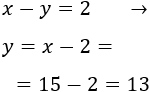
Las edades de los hermanos son 13 y 15.
Problema 13 
La suma de las edades de dos hermanas es 51 y dentro de 5 años, la edad de la pequeña será igual a la actual de la mayor. ¿Qué edades tienen las hermanas?
SOLUCIÓN:
Llamamos \(x\) e \(y\) a las edades actuales de las hermanas. Actualmente, sus edades suman 51:
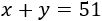
Si dentro de 5 años la pequeña tiene la edad actual de la mayor es porque se llevan 5 años, es decir, la resta de sus edades es 5:
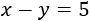
Resolvemos el sistema por reducción sumando las ecuaciones:
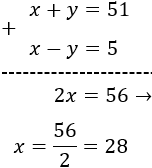
Calculamos la otra incógnita:
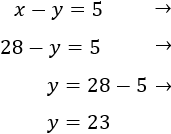
Las edades de las hermanas son 23 y 28.
Problema 14 
Dentro de 10 años, la edad del padre de Alberto será el doble que la suya y dentro de 25 años, Alberto tendrá la edad actual de su padre. ¿Qué edad tiene Alberto?
SOLUCIÓN:
Llamaremos \(x\) a la edad del padre e \(y\) a la de Alberto.
Dentro de 10 años, la edad del padre es el doble que la del hijo:
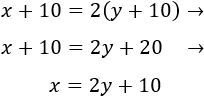
Y dentro de 25 años, Alberto tendrá la edad actual de su padre:
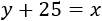
Resolvemos el sistema por igualación:
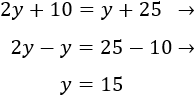
Calculamos la otra incógnita:
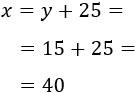
Alberto tiene 15 años.
Problema 15 
Cinco años atrás, la edad de Pedro era el triple que la de Javier y, dentro de dos años, la edad de Pedro será el doble que la de Javier. ¿Cuántos años se llevan Pedro y Javier?
SOLUCIÓN:
Llamamos \(x\) a la edad de Pedro e \(y\) a la de Javier.
Hace cinco años, la edad de Pedro era el triple que la de Javier:
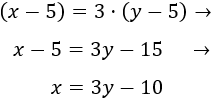
Y dentro de dos años, la edad de Pedro será el doble que la de Javier:
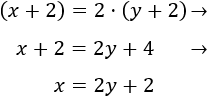
Resolvemos el sistema por igualación:
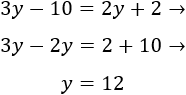
De donde
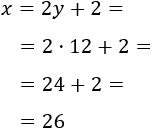
La resta de las edades es
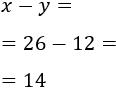
Se llevan 14 años.
Problema 16 
Dentro de 5 años, la edad de Olivia será la edad actual de Jaime y, dentro de 10 años, la suma de sus edades será 67. ¿Qué edad tiene Olivia?
SOLUCIÓN:
Sean \(x\) la edad actual de Olivia e \(y\) la de Jaime.
Dentro de 5 años, la edad de Olivia es la actual de Jaime:
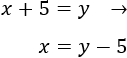
Dentro de 10 años, sus edades suman 67:
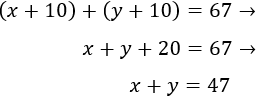
Sustituimos la expresión de \(x\) obtenida de la primera ecuación:
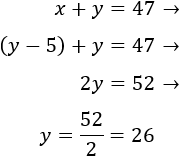
Calculamos \(x\):
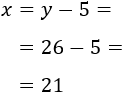
La edad de Olivia es 21.
Problema 17 
En el año 1950, la edad de Maite era el triple que la de Rosana y en el año 1970 la suma de sus edades era 80. Calcular la edad de Maite y la de Rosana en el año 1955.
SOLUCIÓN:
Este problema lo vamos a resolver con tan sólo una incógnita y con la ayuda de una tabla. Llamaremos \(x\) a la edad de Rosana en 1950.
Escribimos una tabla con las edades de ambas en cada año:

En el año 1970, la edad de Rosana es \(x + 20\) y la de Maite es \(3x+20\) porque han pasado 20 años desde 1950.
Como la suma de las edades en 1970 es 80,
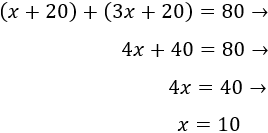
Conociendo \(x\), ya podemos reescribir la tabla:

En el año 1955, la edad de Rosana es 15 y la de Maite es 35.
Problema 18 
Dentro de 10 años, la edad de Emiliano será el doble que la edad actual de Luciana y al año que viene, sus edades sumarán 31. ¿Qué edad tiene cada uno?
SOLUCIÓN:
Llamamos \(x\) a la edad actual de Emiliano e \(y\) a la de Luciana.
Dentro de 10 años, la edad de Emiliano será el doble que la actual de Luciana:
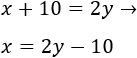
Al año que viene, la suma de sus edades será 31:
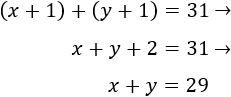
Sustituyendo la \(x\) obtenida de la primera ecuación en la última,
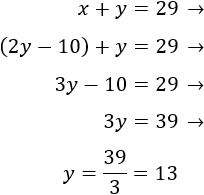
Calculamos \(x\):
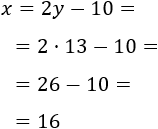
Emiliano tiene 16 años y Luciana tiene 13.
Problema 19 
David tendrá la edad actual de su primo Sebastián dentro de 6 años y la edad de Sebastián será el doble que la edad actual de David. ¿Qué edades tienen los primos?
SOLUCIÓN:
Sean \(x\) y \(y\) las edades actuales de David y de su primo, respectivamente.
Dentro de 6 años, la edad de David será la actual de Sebastián:
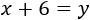
Y la edad de Sebastián será el doble que la actual de David:
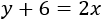
Sustituimos la expresión de \(y\) de la primera ecuación en la segunda:
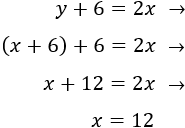
Calculamos \(y\):
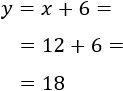
La edad de David es 12 y la de su primo es 18.
Problema 20 
Calcular cuántos años tienen que pasar para que la edad de Andrés sea el doble que la de su sobrino sabiendo que se llevan 14 años y que hace dos años la edad de Andrés era el triple que la de su sobrino.
SOLUCIÓN:
Llamamos \(y\) a la edad actual del sobrino. Entonces la edad actual de Andrés es \(y+14\).
Dentro \(x\) años, Andrés tendrá \(y+14+x\) años y su sobrino tendrá \(y+x\). Queremos que la edad de Andrés sea el doble:
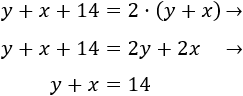
Hace dos años, la edad de Andrés era la edad actual menos 2:
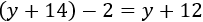
y la de su sobrino también era dos unidades menor:
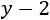
Como la edad de Andrés era el triple,
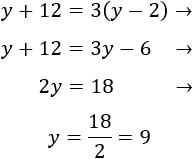
Por tanto, la edad actual del sobrino es 9 y la de su tío es \(9+14 = 23\).
Calculamos \(x\):
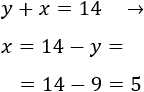
Luego tienen que pasar 5 años.
Problema 21 
La edad de Miguel era el doble que la edad que tenía Samuel cuando Miguel tenía la edad actual de Samuel. Cuando Samuel tenga la edad de Miguel, sus edades sumarán 112. ¿Cuántos años se llevan Miguel y Samuel?
SOLUCIÓN:
Incógnitas:
-
\(x\) es la edad actual de Miguel,
-
\(y\) es la edad actual de Samuel.
Si Miguel es \(a\) años mayor que Samuel (es decir, se llevan \(a\) años de edad), entonces
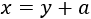
Observad que hace \(a\) años
-
la edad de Miguel era \(x-a\), es decir, \(y\)
-
la edad de Samuel era \(y-a\),
-
la edad de Miguel era la actual de Samuel.
Cuando Miguel tenía la edad actual de Samuel (es decir, hace \(a\) años), la edad de Miguel era el doble que la de Samuel:
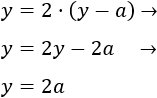
Y como \(x = y+a\), entonces
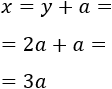
Dentro de \(a\) años,
-
la edad de Miguel será \(x+a\),
-
la edad de Samuel será \(y+a\).
Cuando Samuel tenga la edad actual de Miguel (es decir, dentro de \(a\) años), sus edades sumarán 112:
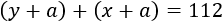
Sustituimos \(y = 2a\) y \(x = 3a\):
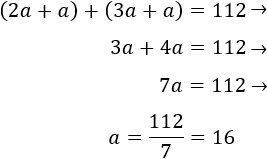
Luego Miguel y Samuel se llevan 16 años. Las edades actuales de Miguel y Samuel son 48 y 32.
Tabla resumen:
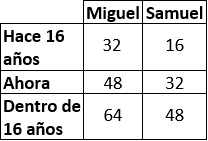
Comprobamos la solución:
-
Cuando Miguel tenía la edad actual de Samuel (32), la edad de Miguel (32) era el doble que la de Samuel (16).
-
Cuando Samuel tenga la edad actual de Miguel (48), la suma de sus edades es 64 + 48 = 112.
Problemas difíciles
Como lo importante de estos problemas es el planteamiento, omitiremos los pasos de la resolución del sistema.
Nota: en algunos problemas de los siguientes, las incógnitas serán también las cifras de números. Por ejemplo, el número 19ab (donde a y b son cifras) también se puede escribir como
$$1000 + 900 + 10\cdot a + b $$
En ocasiones escribiremos una u otra forma para referirnos al número de 4 cifras 19ab, por lo que no hay que confundir el número de 4 cifras 19ab con la operación 19·a·b.
Problema 22 
La edad de Carlota es el número de dos cifras xy y la de Lucas es yx. Calcular sus edades sabiendo que suman 55, que restan 9 y que Carlota es la mayor de los dos.
SOLUCIÓN:
Para poder operar, vamos a reescribir las edades. En el número de dos cifras \(xy\), \(x\) es el número de decenas e \(y\) el de unidades, así que
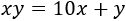
De forma análoga,
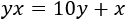
La suma de las edades es 55:
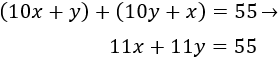
Y la resta es 9:
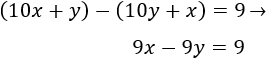
Nota: como Carlota es la mayor, hemos restado la edad de Lucas a la de Carlota. Si lo hacemos al revés, obtendremos las edades intercambiadas.
Tenemos el sistema
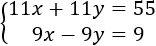
Cuya solución es
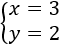
La edad de Carlota es 32 y la de Lucas es 23.
Problema 23 
La edad de Joaquín y la de su vecino Miguel son números de dos cifras y al cambiar el orden de las cifras de la edad de Joaquín se obtiene la edad de Miguel. Sabemos que la suma de las cifras de la edad de Joaquín es 8 y que dentro de una década la edad de Joaquín será la mitad que la de Miguel. ¿Cuáles son sus edades?
SOLUCIÓN:
Si la edad de Joaquín es el número \(xy\), siendo \(x\) la primera cifra e \(y\) la segunda, entonces la edad de Miguel es \(yx\).
Tened en cuenta que \(xy\) no es el producto \(x\cdot y\).
La suma de las cifras de la edad de Joaquín es
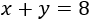
Para poder operar con las edades, podemos escribir el número de dos cifras \(xy\) como
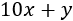
Análogamente, el número \(yx\) lo escribimos como
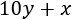
Dentro de 10 años, la edad de Joaquín será
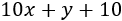
Y la de Miguel será
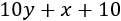
Dentro de 10 años, la edad de Joaquín será la mitad que la de Miguel:
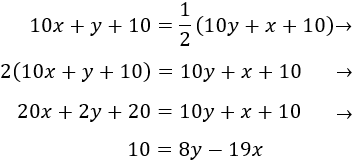
El sistema del problema es
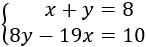
La solución del sistema es
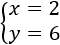
Por tanto, la edad de Joaquín es 26 y la de su vecino es 62.
Problema 24 
Calcular el año de nacimiento de Rosa sabiendo que:
Nota: las letras a y b representan cifras de números, así que los números ab y ba no son los productos \(a\cdot b\) ni \(b\cdot a\).
Ver solución
Antes que nada, observad que podemos escribir el año 19ab como
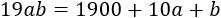
Y los números de dos cifras \(ab\) y \(ba\) son
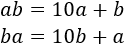
Como en 1930 su edad era \(ab\), tenemos
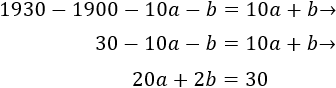
Y como en 1966, su edad es \(ba\),
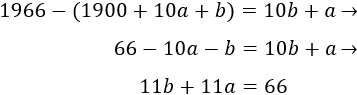
El sistema del problema es
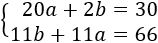
Y su solución es
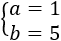
Rosa nació en el año 1915.
Problema 25 
Sofía nació en el año 19ab. En el año 2010, su edad fue el número de dos cifras ba y en el año 2011, su edad coincidió con la suma de las cifras del año de su nacimiento. ¿En qué año nació?
Ver solución
En el año 2010, su edad era el número de dos cifras ba. Este número puede escribirse como
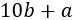
La suma de las cifras del año de su nacimiento es
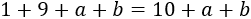
Por tanto, en el año 2011 su edad era \(10+a+b\).
Como de 2010 a 2011 hay un año, en 2011 su edad era una unidad mayor que en 2010. Por tanto,
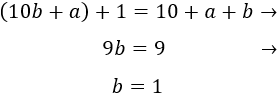
Su año de nacimiento fue 19a1. Y en 2010, su edad era 1a.
El año 19a1 puede escribirse como
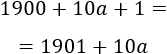
Como en el año 2010 su edad era \(1a= 10+a\), tenemos
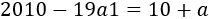
Es decir,
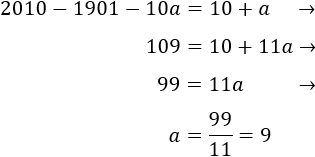
Sofía nació en el año 1991.
Problema 26 
La edad de un determinado presidente de EE. UU. cumple las siguientes características:
-
En el año 19AB, su edad coincide con la suma de las cifras de dicho año.
-
En el año 1944, su edad es el doble que en el año 19AB.
-
En el año 19BA, su edad es el triple que en año 19AB.
Calcular el año de nacimiento del presidente.
Ver solución
En el año 19AB, su edad es
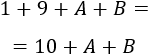
En el año 1944, su edad es
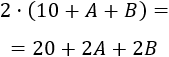
En el año 19BA, su edad es
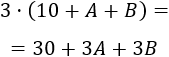
Para poder operar con el número 19AB o con el número 19BA, los escribimos como sigue:
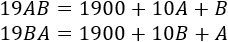
La diferencia entre dos años es igual a la diferencia entre las respectivas edades en dichos años. Por tanto, tenemos, por ejemplo, las ecuaciones
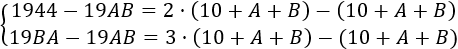
Operando un poco en el lado derecho de las ecuaciones anteriores obtenemos:
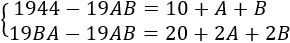
Escribiendo los años del modo que hemos dicho anteriormente,
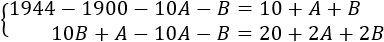
Simplificamos las ecuaciones:
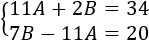
La solución del sistema anterior es
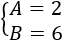
Sabemos, por el apartado a, que en el año 1926 la edad del presidente era 18. Por tanto, su año de nacimiento fue 1908:
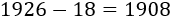
El presidente de EE.UU. que nació en 1908 fue Lyndon Baines Johnson (LBJ).
Problemas con sistemas de ecuaciones NO lineales
Como en estos problemas tenemos sistemas de ecuaciones no lineales, mostraremos su resolución. Normalmente, despejaremos una de las incógnitas en una de las ecuaciones para sustituirla en la otra ecuación.
Problema 27 
El producto de las edades de dos hermanos es 162 y su cociente es 2. ¿Cuántos años tienen?
Ver solución
Si las edades son \(x\) e \(y\), su producto es
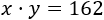
Y su cociente es
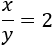
El sistema de ecuaciones no lineales es
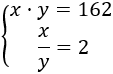
Despejamos la \(x\) de la segunda ecuación:
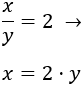
Y sustituimos en la primera ecuación:
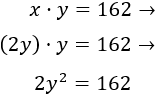
Resolvemos la ecuación de segundo grado:
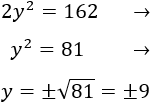
Como \(y\) representa una edad, debe ser no negativo. Por tanto, \(y = 9\).
Calculamos \(x\) a partir de \(y = 9\):
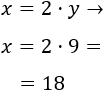
La solución del sistema es
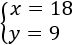
Sus edades son 9 y 18 años.
Problema 28 
La edad de Ana María es el cuadrado de la edad de su hija. Además, dentro de 9 años, su edad será el triple que la de su hija. ¿Qué edad tiene Ana María?
Ver solución
Si \(x\) es la edad de Ana María e \(y\) la de se hija, entonces, la primera ecuación que tenemos es
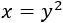
Dentro de 9 años, la edad de Ana María es \(x+9\) y la de su hija es \(y+9\). Para entonces, su edad será el triple que la de su hija:
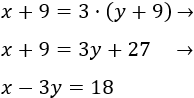
El sistema de ecuaciones no lineales esv
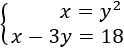
Sustituimos la \(x\) por \(y^2\) en la segunda ecuación y resolvemos la ecuación de segundo grado:
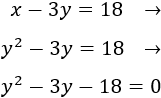
Las soluciones son \(y = -3\) e \(y = 6\). Como \(y\) representa una edad, no puede ser negativa. Por tanto, la edad de la hija\(y = 6\) y la de la madre es \(6^2 = 36\).
Problema 29 
Sandro y Ezequiel son hermanos y el producto de sus edades es igual a la edad de su padre. Sandro es 8 años menor que Ezequiel y la suma de su edad y la de su padre es igual a 36. ¿Qué edad tiene Ezequiel?
Ver solución
Si \(x\) es la edad de Sandro, entonces la de su hermano es \(x+8\). Si llamamos \(y\) a la edad del padre, entonces,
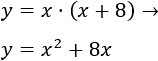
La suma de la edad de Sandro y la de su padre es 36:
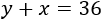
El sistema de ecuaciones no lineales es
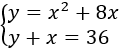
Restamos ambas ecuaciones:
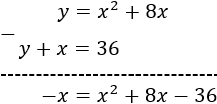
Tenemos la ecuación de segundo grado
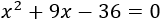
Cuyas soluciones son \( x = -12\) y \(x = 3\). La primera no nos sirve por ser negativa. Por tanto, la edad de Sandro es 3 y la de Ezequiel es 11.
Aunque no es necesario, calculamos la otra incógnita:
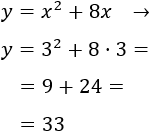
Problema 30 
Aurelio, Carlos y José son hermanos. José es el mayor de los tres y su edad es igual a la suma de los cuadrados de las edades de sus hermanos. Dentro de un año, la edad de Carlos será el doble que la de Aurelio y dentro de 22 años, la edad del mayor será igual a la suma de las edades de sus hermanos. ¿Qué edad tiene José?
Ver solución
Llamamos \(x\) y \(y\) a las edades actuales de Aurelio y de Carlos, respectivamente. La edad de José es
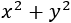
Al año que viene, la edad de Aurelio será \(x+1\) y la de Carlos será \(y+1\) y, además, la edad de Carlos será el doble que la de Aurelio:
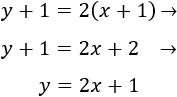
Dentro de 22 años, las edades de los tres hermanos serán \(x+22\), \(y+22\) y \(x^2+y^2+22\) y debe cumplirse
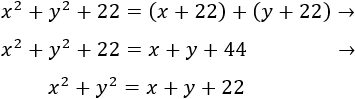
El sistema de ecuaciones no lineales es
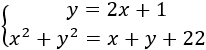
Sustituimos \(y = 2x+1\) en la segunda ecuación y la resolvemos:
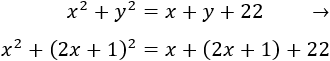
Antes de seguir, calculamos el cuadrado \((2x+1)^2\):
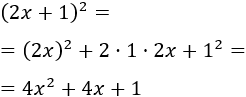
Por tanto, la ecuación que queda es
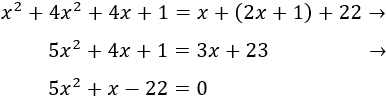
Las soluciones son \(x =-11/5\) y \(x = 2\). La primera no nos sirve por ser negativa.
La edad de Aurelio es 2 y para calcular la de José necesitamos calcular la incógnita \(y\):
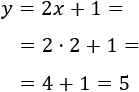
Calculamos la edad de José:
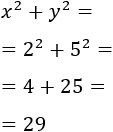
José tiene 29 años.
Problema 31 
La suma de la edad de Gerardo y la de su sobrino es 38. Dentro de 5 años, la edad del Gerardo será la octava parte del cuadrado de la edad de su sobrino. ¿Qué edad tiene Gerardo?
Ver solución
Sean \(x\) la edad de Gerardo e \(y\) la de su sobrino. La suma de sus edades es 38:
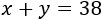
Dentro de 5 años, sus edades serán \(x+5\) e \(y+5\) y se cumplirá
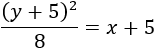
El sistema de ecuaciones no lineales es
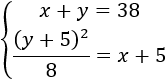
Operamos un poco en la segunda ecuación:
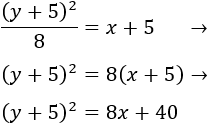
Calculamos el binomio al cuadrado en la ecuación:
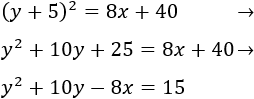
De la primera ecuación del sistema tenemos
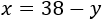
Sustituimos la \(x\) en la ecuación calculada anteriormente*:
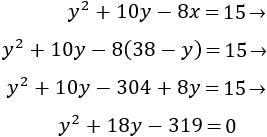
Nota*: si en lugar de sustituir \(x = 38-y\) sustituimos \(y = 38-x\), entonces los cálculos son mucho más largos.
Las soluciones de la ecuación de segundo grado son \(y = 11\) e \(y = -29\). La segunda no es válida.
Calculamos \(x\):
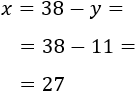
Luego la edad Gerardo es 27 y la de su sobrino es 11.
Problema 32 
El producto de las edades actuales de dos amigos es 42 y dentro de 5 años será 132. ¿Qué edades tienen?
Ver solución
Si las edades son \(x\) e \(y\), su producto es
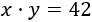
Dentro de 5 años, las edades de los amigos serán
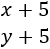
Y su producto será
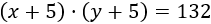
El sistema de ecuaciones no lineales es
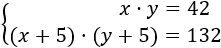
Despejamos la \(x\) en la primera ecuación:
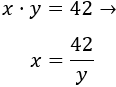
Sustituimos \(x\) en la segunda ecuación:
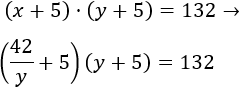
Vamos a calcular el producto del lado izquierdo de la igualdad (multiplicando uno a uno los monomios de los paréntesis) para simplificar la ecuación:
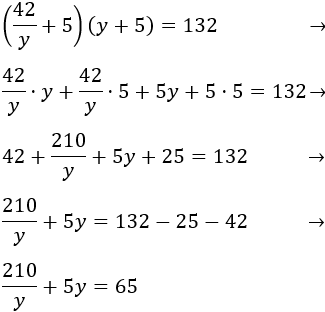
Para poder resolver la ecuación anterior, la multiplicamos por \(y\), así desaparece el denominador, transformándose la ecuación en una ecuación de segundo grado (y apareciendo, por tanto, una solución extra):
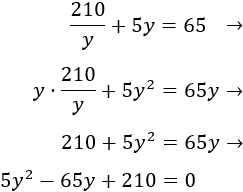
Las soluciones de la ecuación de segundo grado son \(y=6\) e \(y = 7\) (omitimos el procedimiento por su simplicidad).
Si \(y = 6\), entonces \(x\) es
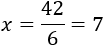
Si \(y = 7\), entonces \(x\) es
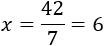
Los hermanos tienen 6 y 7 años.