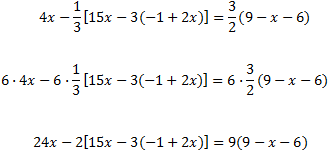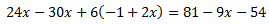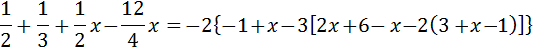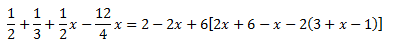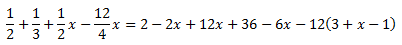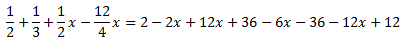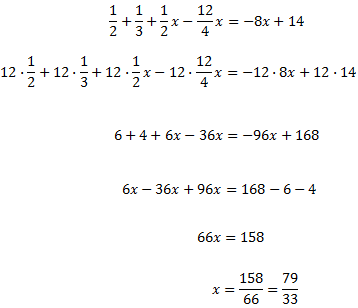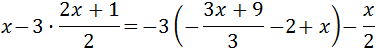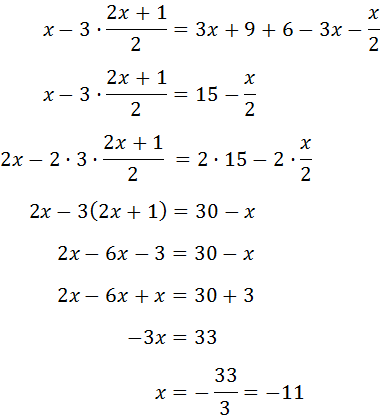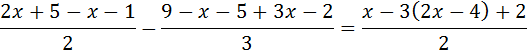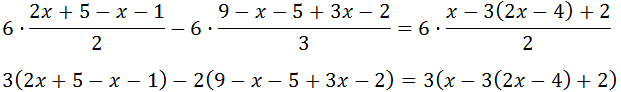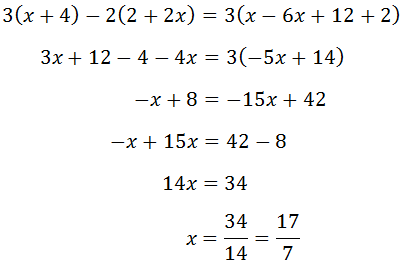A continuación se resuelven ecuaciones de primer grado cuya dificultad va aumentado: ecuaciones simples, con fracciones (donde usaremos el mínimo común múltiplo), con paréntesis y con paréntesis anidados
(unos dentro de otros).
En la Parte I, las ecuaciones son más cortas y se explican todos los
pasos. Pretenden estar ordenadas de menor a mayor dificultad. En la Parte II, las ecuaciones son un poco más complicadas; y, en la Parte III, se muestran todas las operaciones y pasos, pero no se explican tan
detalladamente.
Parte I (6 ecuaciones)
Ecuación I.1: ecuación básica 
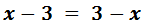
Resolvemos:
Pasamos las x's a un lado de la igualdad
(izquierda) y los números al otro lado (derecha):
En la derecha, la x está restando. Pasa a la izquierda sumando:
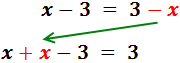
Sumamos los monomios con x’s:
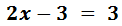
En la izquierda, el -3 está restando. Pasa a la derecha sumando:
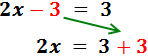
Sumamos los monomios de la derecha:
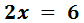
El coeficiente de la x es 2. Este número está multiplicando a x, así
que pasa al otro lado dividiendo:
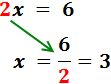
Por tanto, la solución de la ecuación es x = 3.
Ecuación I.2: ecuación con paréntesis 
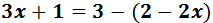
Resolvemos:
Recordamos que los paréntesis sirven para agrupar elementos,
para simplificar o para evitar ambigüedades.
El signo negativo de delante del paréntesis indica que los monomios que
contiene tienen que cambiar de signo:
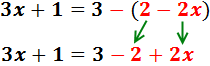
Sumamos 3 y -2 en el lado derecho:
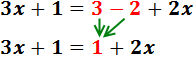
Pasamos los monomios con x’s a la
izquierda y los números a la derecha:
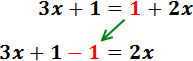
Sumamos 1 y -1. Como el resultado es 0, no lo escribimos:
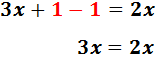
Pasamos 2x a la izquierda restando y sumamos los monomios:
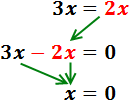
Luego la solución de la ecuación es x = 0.
Ecuación I.3: ecuación con fracciones 
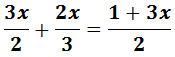
Resolvemos:
Tenemos varias formas de proceder con las fracciones:
- Sumar las fracciones de forma habitual.
- Multiplicar la ecuación por el mínimo común
múltiplo de los denominadores.
En esta ecuación aplicaremos la segunda opción.
De este modo los denominadores van a desaparecer.
Multiplicamos, pues, por m.c.m.(2, 3) = 6:
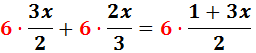
Para simplificar, calculamos las divisiones:
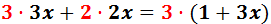
Nótese que hemos escrito un paréntesis al eliminar la fracción de la derecha. Esto se debe a que el 3 debe multiplicar al
numerador que está formado por una suma.
Calculamos los productos:
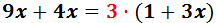
Para eliminar el paréntesis, multiplicamos por 3 todos los elementos que contiene:
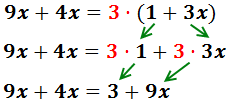
Pasamos las x’s a la izquierda:
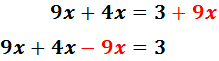
Sumamos los monomios:
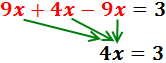
Finalmente, el coeficiente de la x pasa dividiendo al otro lado:
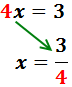
La solución de la ecuación es x = 3/4.
La fracción no se puede simplificar más puesto
que ya es irreductible (el máximo común divisor del numerador
y del denominador es 1).
Ecuación I.4: ecuación sin solución 
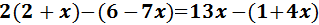
Resolvemos:
Eliminamos los paréntesis:
El de la izquierda tiene un 2 delante, por lo que
multiplicamos su contenido por 2.
Los otros dos paréntesis tienen un signo negativo delante,
así que cambiamos los signos de sus monomios:
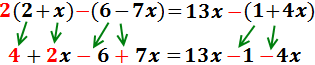
Para simplificar, en cada lado sumamos los monomios con y sin
parte literal (los que tienen x y los que no):
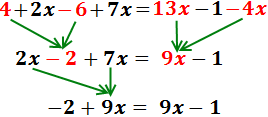
Pasamos las x’s al lado izquierdo y sumamos:
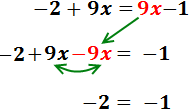
Hemos obtenido una igualdad falsa: -2 = -1. Esto significa que la ecuación nunca se cumple, sea cual sea el
valor de x. Por tanto, la ecuación no tiene solución.
Ecuación I.5: ecuación con infinitas soluciones 
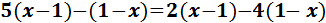
Resolvemos:
Eliminamos los paréntesis multiplicando sus sendos
contenidos por el número que tienen delante.
No hay que olvidar que si el número de delante es
negativo, también hay que cambiar los signos:
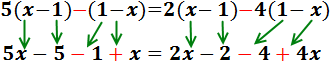
En cada lado, sumamos los monomios según su parte literal:
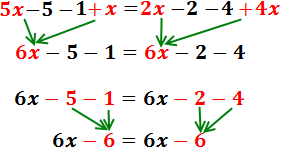
Pasamos las x’s a la izquierda y los números a la derecha:
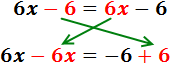
Sumamos los monomios:
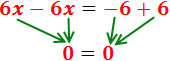
Hemos obtenido una igualdad que siempre se
cumple: 0 = 0. Esto significa que la ecuación se
cumple siempre, independientemente del valor de x.
Por tanto, la ecuación tiene infinitas soluciones
(x puede ser cualquier número y hay infinitos números).
Podemos expresarlo como “x es cualquier real”:
$$ x \in \mathbb{R} $$
Ecuación I.6: ecuación con paréntesis anidados 
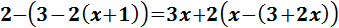
Resolvemos:
Primero eliminaremos los paréntesis exteriores.
Empezamos por el de la izquierda. Este paréntesis
tiene un signo negativo delante, por lo que cambiamos el signo a
sus sumandos. Uno de los sumandos es otro paréntesis:
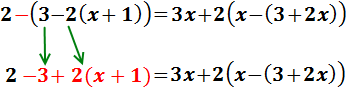
Eliminamos el paréntesis que queda en la izquierda multiplicando por 2:
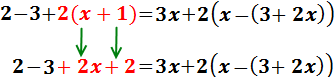
Sumamos los números en el lado izquierdo para simplificar:
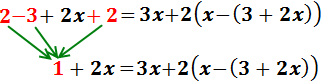
Eliminamos el paréntesis exterior de la derecha multiplicando sus sumandos por 2:
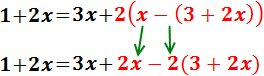
Eliminamos el paréntesis que queda multiplicando por 2 y cambiando los signos:
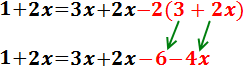
Sumamos los monomios en el lado derecho:
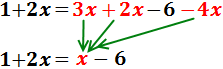
Pasamos las x’s a la izquierda, los números a la
derecha y simplificamos:
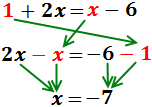
Por tanto, la solución es x = -7.
Parte II (7 Ecuaciones)
Ecuación II.1 
$$ 3(x+1) -2x = $$
$$ = x-\left( 2 + 3(3 - x)\right) $$
Resolvemos:
En esta ecuación tenemos paréntesis anidados (uno dentro de otro).
Vamos primero a quitar el pequeño (el de dentro). Éste está multiplicado por
3. Para quitar el paréntesis, tenemos que multiplicar por 3 todos los sumandos de dentro:
$$ 3(x+1) -2x = x-\left( 2 + 3\cdot 3 -3x\right) $$
$$ 3(x+1) -2x = x-\left( 2 + 9 -3x\right) $$
$$ 3(x+1) -2x = x-\left( 11 -3x \right) $$
El interior del paréntesis ya no se puede simplificar más. Como tiene un signo negativo dentro,
cambiamos el signo de los sumandos de dentro:
$$ 3(x+1) -2x = x - 11 +3x $$
$$ 3(x+1) -2x = - 11 +4x $$
El paréntesis del lado izquierdo está multiplicado por 3. Para quitarlo, multiplicamos todos
los sumandos de dentro por 3:
$$ 3x +3 -2x = - 11 +4x $$
Ahora sólo tenemos que agrupar los monomios según su parte literal:
$$ x +3 = - 11 +4x $$
$$ x = -3 - 11 +4x $$
$$ x = -14 +4x $$
$$ x -4x = -14 $$
$$ -3x = -14 $$
Para despejar la x tenemos que pasar el -3 dividiendo:
$$ x = \frac{-14}{-3} $$
Como el signo del numerador y del denominador es negativo, desaparecen:
$$ x = \frac{14}{3} $$
Ya no podemos simplificar más la expresión de la solución ya que 14 no
es divisible por 3, es decir, el máximo común divisor de 14 y 3 es 1.
Ecuación II.2 
$$ 1 - 2 ( 1 + 3x - 2(x + 2) + 3x ) = - 1 $$
Resolvemos:
Tenemos paréntesis anidados (uno dentro de otro) y signos negativos delante de ellos.
Antes de trabajar con los paréntesis, podemos sumar los términos 3x y 3x del paréntesis
exterior ya que se encuentran en el mismo nivel (no forman parte de paréntesis distintos):
$$ 1 - 2 ( 1 + 6x - 2(x + 2)) = - 1 $$
Como el paréntesis interno está multiplicado por -2, multiplicamos por -2 sus sumandos para
poder quitarlo:
$$ 1 - 2 ( 1 + 6x - 2x - 4) = - 1 $$
$$ 1 - 2 ( 6x - 2x - 3) = - 1 $$
$$ 1 - 2 ( 4x - 3) = - 1 $$
Procedemos de igual modo que en el paréntesis anterior:
$$ 1 -8x +6 = - 1 $$
$$ -8x +7 = - 1 $$
$$ -8x = -8 $$
$$ x = \frac{-8}{-8} $$
$$ x = 1 $$
Ecuación II.3 
$$ x + \frac{1}{3} \left(x - 3 -\frac{1}{2}\left(4 - 3x\right)\right)= $$
$$ = \frac{2}{3}\left(1-\frac{5x}{2}\right) $$
Resolvemos:
Tenemos paréntesis anidados multiplicados por fracciones, algunas de ellas con signo negativo.
Trabajaremos primero en el lado izquierdo de la igualdad. El paréntesis interior está multiplicado
por una fracción negativa. Para quitar el paréntesis, tenemos que multiplicar los sumandos de dentro por
la fracción:
$$ x + \frac{1}{3} \left(x - 3 -\frac{4}{2} +\frac{3x}{2}\right)= $$
$$ = \frac{2}{3}\left(1-\frac{5x}{2}\right) $$
$$ x + \frac{1}{3} \left(x - 3 -2 +\frac{3x}{2}\right)= $$
$$ = \frac{2}{3}\left(1-\frac{5x}{2}\right) $$
$$ x + \frac{1}{3} \left(x -5 +\frac{3x}{2}\right)= $$
$$ = \frac{2}{3}\left(1-\frac{5x}{2}\right) $$
Notemos que si multiplicamos por 3 toda la ecuación, desaparecen dos denominadores:
$$ 3x + \frac{3}{3} \left(x -5 +\frac{3x}{2}\right)= 3\frac{2}{3}\left(1-\frac{5x}{2}\right) $$
$$ 3x +\left(x -5 +\frac{3x}{2}\right)= 2\left(1-\frac{5x}{2}\right) $$
El paréntesis de la izquierda lo podemos quitar (está multiplicado por 1) y el de la derecha lo quitamos
multiplicando sus sumandos por 2:
$$ 3x + x -5 +\frac{3x}{2}= 2-2\frac{5x}{2} $$
Ahora vamos agrupando los monomios según su parte literal:
$$ 3x + x -5 +\frac{3x}{2}= 2-5x $$
$$ 4x -5 +\frac{3x}{2}= 2-5x $$
$$ 4x +5x +\frac{3x}{2}= 2 + 5 $$
$$ 9x +\frac{3x}{2}= 7 $$
Sumamos las fracciones 9x y 3x/2:
$$ \frac{18x}{2} + \frac{3x}{2}= 7 $$
$$ \frac{21x}{2}= 7 $$
$$ x= \frac{7\cdot 2}{21} $$
Escribimos 21 como un producto para reducir la fracción:
$$ x= \frac{7\cdot 2}{7\cdot 3} $$
Los 7 desaparecen y obtenemos la solución
$$ x= \frac{2}{ 3} $$
Ecuación II.4 
$$ \frac{x}{2} + \frac{2}{3} = \frac{x}{3} + 1 -\frac{1}{2}\left(1-\frac{x+1}{3}\right)$$
Resolvemos:
Tenemos los denominadores 2 y 3. Multiplicamos por su mínimo común múltiplo, 6, para trabajar
sin fracciones:
$$ 6\frac{x}{2} + 6\frac{2}{3} = 6\frac{x}{3} + 6 -6\frac{1}{2}\left(1-\frac{x+1}{3}\right)$$
$$ 3x+ 4 = 2x + 6 -3\left(1-\frac{x+1}{3}\right)$$
$$ 3x-2x+ 4 -6 = -3\left(1-\frac{x+1}{3}\right)$$
$$ x -2 = -3\left(1-\frac{x+1}{3}\right)$$
La fracción que queda tiene un signo negativo delante, lo que supone cambiar el signo del numerador.
Como el numerador es una suma, cambiamos el signo a ambos sumandos:
$$ x -2 = -3\left(1+\frac{-x-1}{3}\right)$$
Realizamos la suma en el interior del paréntesis:
$$ x -2 = -3\left(\frac{3}{3}+\frac{-x-1}{3}\right)$$
$$ x -2 = -3\left(\frac{3-x-1}{3}\right)$$
$$ x -2 = -3\left(\frac{2-x}{3}\right)$$
Tenemos el paréntesis multiplicado por 3, pero su interior está dividido entre 3, así que podemos quitar ambos:
$$ x -2 = -\left(2-x\right)$$
Quitamos el paréntesis cambiando el signo de sus sumandos (ya que hay un signo menos delante)
$$ x -2 = -2 + x$$
$$ x -x -2 = -2$$
$$ -2 = -2 $$
$$ 0 = 0 $$
Como tenemos una igualdad verdadera, la ecuación se cumple independientemente de los valores que
tome x. Por tanto, la solución es todos los reales:
$$ x\in \mathbb{R} $$
Ecuación II.5 
$$ 2\left( x - 3\left( x - 4\left( x -\left( \frac{x}{8}+ 1 \right) \right) \right) \right)=1$$
Resolvemos:
Tenemos múltiples paréntesis anidados, algunos con signo negativo delante.
Comenzamos por el más interno: como tiene un signo menos, para quitarlo cambiamos el signo
de todos sus sumandos
$$ 2\left( x - 3\left( x - 4\left( x -\frac{x}{8}- 1 \right) \right) \right)=1$$
El más interno está multiplicado por -4. Para quitarlo multiplicamos por -4 sus sumandos
(multiplicar por 4 y cambiar el signo)
$$ 2\left( x - 3\left( x -4x +4\frac{x}{8}+4 \right) \right)=1$$
$$ 2\left( x - 3\left( x -4x +\frac{x}{2}+4 \right) \right)=1$$
$$ 2\left( x - 3\left( -3x +\frac{x}{2}+4 \right) \right)=1$$
De nuevo, el paréntesis interno está multiplicado por un número negativo:
$$ 2\left( x+ 9x -3\frac{x}{2} -12 \right)=1$$
$$ 2\left( 10x -\frac{3x}{2} -12 \right)=1$$
Quitamos el último paréntesis:
$$ 20x -2\frac{3x}{2} -24 =1$$
$$ 20x -3x -24 =1$$
$$ 17x =1+24$$
$$ 17x =25$$
$$ x=\frac{25}{17}$$
No podemos reducir más la fracción ya que el máximo común divisor de 25 y 17 es 1 (porque 17 es primo).
Ecuación II.6 
$$ x-\frac{2}{3}\left(-1-\left(\frac{15}{2}-x \right)\right)=\frac{x}{3}+1 $$
Resolvemos:
Multiplicamos toda la ecuación por 3 para eliminar algunas de las fracciones:
$$ 3x-2\left(-1-\left(\frac{15}{2}-x \right)\right)=x+3 $$
El paréntesis interno tiene un signo delante: cambiamos el signo de todos sus sumandos
para poder quitarlo:
$$ 3x-2\left(-1-\frac{15}{2}+x \right)=x+3 $$
El paréntesis está multiplicado por -2. Para quitarlo, multiplicamos sus sumandos por -2 (multiplicar por
2 y cambiar el signo):
$$ 3x+2+2\frac{15}{2}-2x =x+3 $$
$$ 3x+2+15-2x =x+3 $$
Ahora sólo queda agrupar los monomios:
$$ 3x-2x -x =3-2 -15 $$
$$ 0 = -14 $$
Obtenemos una igualdad falsa, independientemente del valor de la incógnita. Esto quiere decir que
no hay ningún valor para el que la ecuación se cumpla: no existe solución.
Ecuación II.7 
$$ \frac{5x}{3} -2 \left( \frac{x}{3}+x \right) =-x $$
Resolvemos:
Quitamos el paréntesis multiplicando por -2 su contenido (multiplicar por 2 y cambiar el signo):
$$ \frac{5x}{3} \frac{-2x}{3}-2x = -x $$
Multiplicamos toda la ecuación por 3 para evitar las fracciones:
$$ 5x -2x-6x = -3x $$
Agrupamos los monomios:
$$ 5x -2x-6x +3x= 0 $$
$$ -3x +3x= 0 $$
$$ 0= 0 $$
Obtenemos una igualdad que siempre es cierta, independientemente del valor de la incógnita. Esto
quiere decir que la ecuación tiene infinitas soluciones: cualquier valor es una solución:
$$ x\in \mathbb{R} $$
Parte III (12 Ecuaciones)
Ecuación III.1 
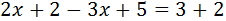
Resolvemos:
Sumamos (o restamos) los monomios con la misma parte literal (las x con x, los números con números). Los que están sumando en un lado, pasan al otro lado restando y viceversa.
Después pasamos las x a un lado de la igualdad y los números a la otra.
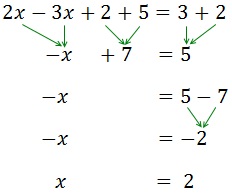
Ecuación III.2 
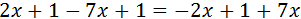
Resolvemos:
Los elementos que están sumando en un lado, pasan al otro lado restando y viceversa.
Después pasamos las x a un lado de la igualdad y los números a la otra.
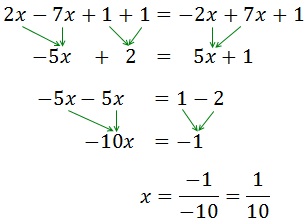
Como la x tiene un coeficiente (-10), que está multiplicando, éste pasa al otro lado dividiendo.
Ecuación III.3 
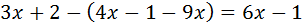
Resolvemos:
Primero nos deshacemos del paréntesis: como tiene un signo negativo delante, cambiamos el signo a todos los elementos de su interior.
Luego sólo tenemos que agrupar las x en un lado y los números en el otro.
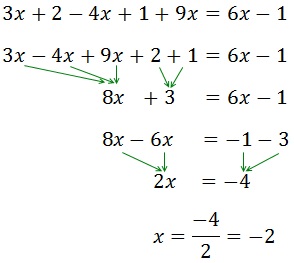
Como la x tiene un coeficiente (2) multiplicando, éste pasa al otro lado dividiendo.
Ecuación III.4 
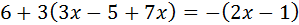
Resolvemos:
Primero nos deshacemos de los paréntesis: el de la
derecha tiene un signo negativo, que cambia el signo de los
elementos del interior; el de la derecha
está multiplicado por 3, que pasa dentro del paréntesis
multiplicando a todos los elementos.
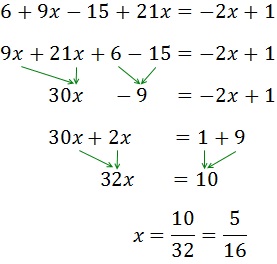
Ecuación III.5 
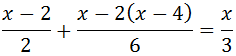
Resolvemos:
Tenemos fracciones. Podemos proceder de varias formas:
- multiplicar todos los términos de la ecuación por el mínimo común múltiplo de los denominadores
- o bien, ir multiplicando por cada denominador .
Nosotros multiplicamos toda la ecuación por el mínimo común múltiplo, que es 6:
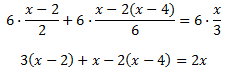
De este modo, al efectuar la división, desaparecen los denominadores.
Ahora nos deshacemos de los paréntesis: el primero está multiplicado por 3, por lo que multiplicamos por 3 su contenido; el segundo por -2, por lo que multiplicamos por -2 (no olvidar el signo):
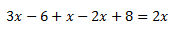
Finalmente, agrupamos las x a un lado y los números al otro:
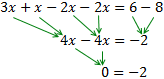
Tenemos 0 = -2, lo cual es una igualdad falsa. Por tanto, la ecuación no tiene solución porque sea cual sea el valor de x, llegamos a una relación (igualdad) absurda.
Ecuación III.6 
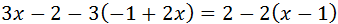
Ver Solución
Los números que multiplican a los paréntesis son negativos, con lo que al multiplicar su contenido por éstos, todos los elementos cambian de signo.
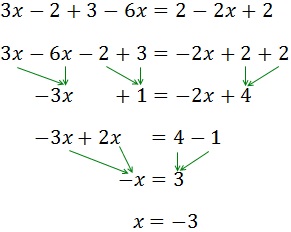
Ecuación III.7 
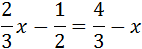
Ver Solución
Como tenemos denominadores, multiplicamos toda la ecuación por el mínimo común múltiplo de éstos, que es 6:
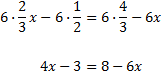
De este modo, al efectuar las divisiones, desaparecen los denominadores.
Ahora sólo falta agrupar las x a un lado y los números al otro.
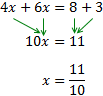
Ecuación III.8 
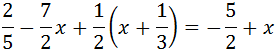
Ver Solución
Como tenemos denominadores, multiplicamos toda la ecuación por el mínimo común múltiplo de estos, que es 30:
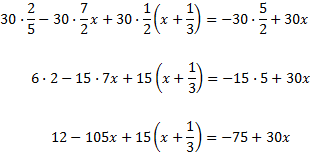
Sólo tenemos un paréntesis, que está multiplicado por 15. Para quitarlo, multiplicamos su contenido por 15:
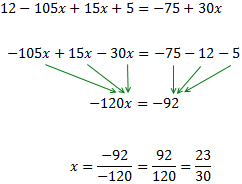
Ecuación III.9 
![ecuación de primer grado con paréntesis anidados (uno dentro de otro): 4x - (1/3)[15x-3(-1+2x)] = (3/2)(9-x-6) ecuaciones de primer grado resueltas](https://www.matesfacil.com/ESO/Ecuaciones/Ecua9.jpg)
Ver Solución
En la ecuación tenemos paréntesis anidados (unos dentro de otros) y multiplicados por fracciones. Pero antes de ocuparnos de esto, multiplicamos toda la ecuación por el mínimo común múltiplo de los denominadores, que es 6:
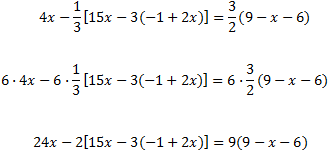
Ahora vamos a los paréntesis:
En la izquierda hay dos, pero lo tratamos como si fuera sólo uno. Es decir, multiplicamos todo su contenido por -2.
Al mismo tiempo, en la derecha, multiplicamos el contenido por 9:
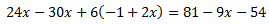
Nos queda un paréntesis, que está multiplicado por 6:
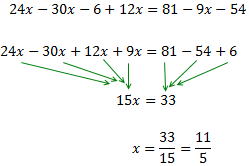
Ecuación III.10 
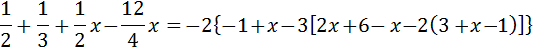
Ver Solución
Como tenemos paréntesis anidados (uno dentro de otro), vamos a ir quitándolos.
El primer paréntesis (el exterior), está multiplicado por -2. Para quitarlo, multiplicamos todo su contenido por -2:
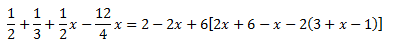
Ahora, el paréntesis exterior está multiplicado por 6. Para quitarlo, multiplicamos su contenido por 6:
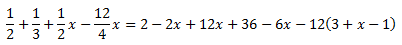
Por último, el paréntesis que queda está multiplicado por -12, por lo que para quitarlo multiplicamos por -12 su contenido:
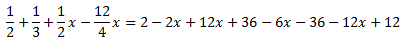
Ahora vamos a deshacernos de las fracciones, pero antes, sumamos algunos elementos para no tener una expresión tan larga:
Multiplicamos toda la ecuación por el mínimo común múltiplo de los denominadores, que es 12:
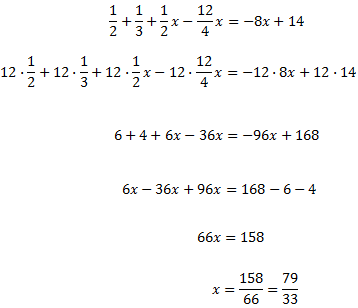
Ecuación III.11 
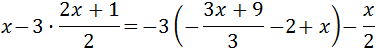
Ver Solución
Multiplicaremos la ecuación por 2 para eliminar los denominadores:
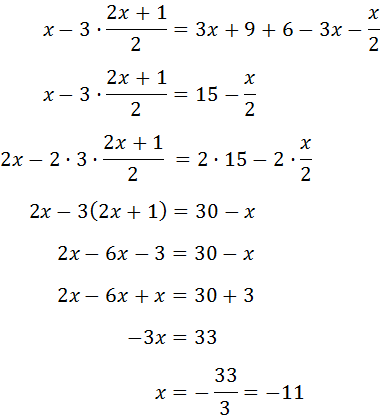
Ecuación III.12 
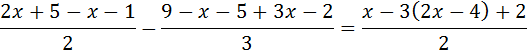
Ver Solución
Multiplicamos toda la ecuación por el mínimo común múltiplo de los
denominadores: 6
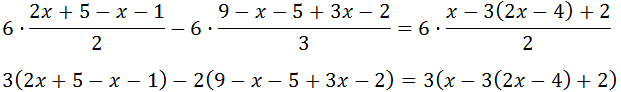
Eliminamos los paréntesis:
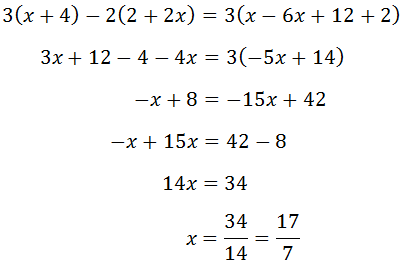
Más ecuaciones resueltas: Ecuaciones de primer grado (PyE) y Ecuaciones Resueltas .com.


Ecuaciones de primer grado resueltas -
© -
matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.








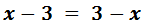
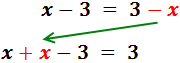
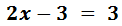
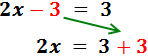
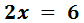
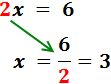
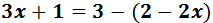
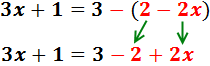
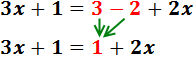
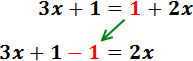
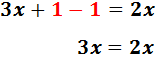
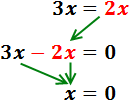
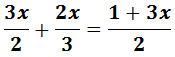
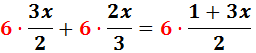
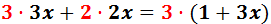
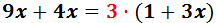
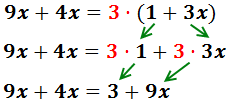
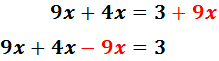
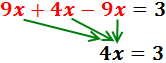
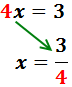
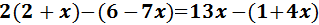
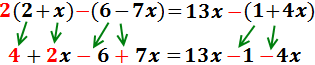
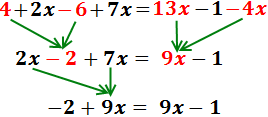
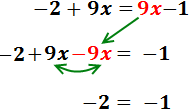
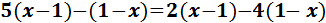
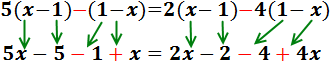

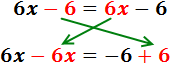
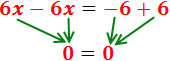

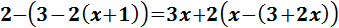
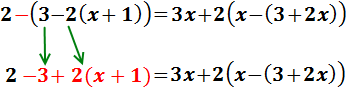
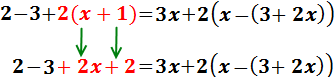
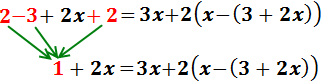
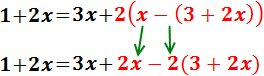
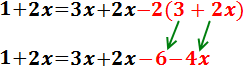
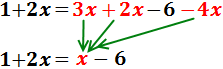

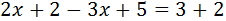

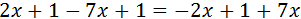
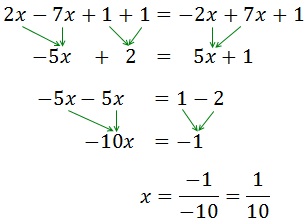
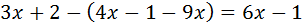
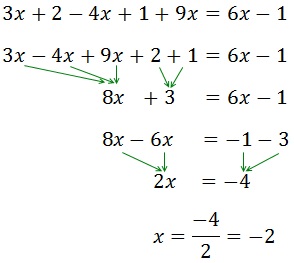
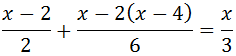
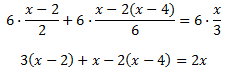
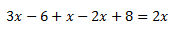
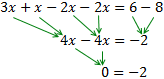
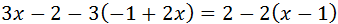
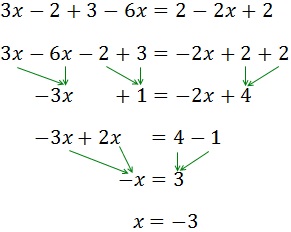
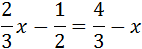
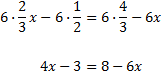
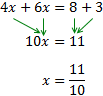
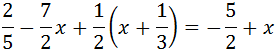
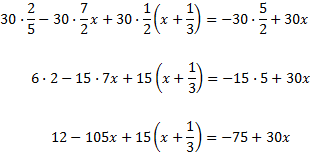
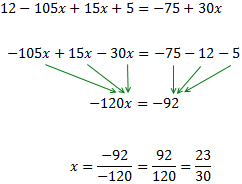
![ecuación de primer grado con paréntesis anidados (uno dentro de otro): 4x - (1/3)[15x-3(-1+2x)] = (3/2)(9-x-6) ecuaciones de primer grado resueltas](https://www.matesfacil.com/ESO/Ecuaciones/Ecua9.jpg)