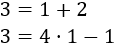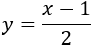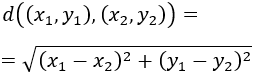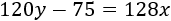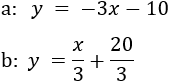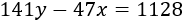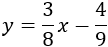Contenido de esta página:
-
Introducción
-
Recordatorio
-
Rectas paralelas
-
Rectas perpendiculares
-
20 Problemas Resueltos
1. Introducción
En esta página estudiamos los conceptos de rectas paralelas y de rectas perpendiculares (nivel de secundaria). Para poder comprender y resolver los problemas, el alumno necesitará tener las siguientes destrezas:
Saber interpretar o representar en el plano la gráfica de una recta.
Saber encontrar la ecuación de la recta que pasa por dos puntos.
Resolver ecuaciones de primer grado.
Antes de abordar los problemas, haremos un pequeño recordatorio de los conceptos que necesitaremos.
2. Recordatorio
Contenido de esta sección:
-
Ecuación de una recta
-
Puntos de una recta
-
Pendiente de una recta
Ver texto
1. Ecuación de una recta
La ecuación de una recta del plano real en su forma general es
$$ y = ax + b $$
Los coeficientes \(a\) y \(b\) son constantes y se denominan pendiente de la recta y ordenada en el origen, respectivamente.
Las rectas verticales son un caso especial ya que su ecuación es de la forma
$$ x = k $$
Para más información sobre rectas: rectas y parábolas.
2. Puntos de una recta
Únicamente diremos que una recta está formada por infinitos puntos del plano.
Escribiremos los puntos como \(P=(x_0,y_0)\), donde \(x_0\) es la primera coordenada e \(y_0\) es la segunda.
Los infinitos puntos que forman una recta tienen algo en común: cumplen la ecuación de dicha recta.
Es decir, si \(P=(x_0,y_0)\) es un punto de la recta \(y = ax+b\), entonces se cumple
$$ y_0 = a\cdot x_0 + b $$
3. Pendiente de una recta
Hemos dicho en anteriormente que dada la ecuación de la recta \(y = ax+b\), el coeficiente \(a\) se denomina pendiente.
La pendiente de una recta es la responsable de su inclinación: cuanto mayor es, más rápido crece y, por tanto, más inclinada está la recta.
Si tenemos dos puntos de una recta, también podemos calcular la pendiente de dicha recta sin necesidad de calcular la ecuación de la misma:
Dados dos puntos \(A = (x_1,y_1)\) y \(B=(x_2,y_2)\), la pendiente de la recta que los une es
$$ m = \frac{y_2-y_1}{x_2-x_1} $$
Nota: no se puede aplicar la fórmula anterior si la primera coordenada de los puntos coinciden (\(x_2=x_1\)). En este caso, la recta que une a los puntos es la recta vertical \( x = x_1\).
3. Rectas paralelas
Definición 1:
En el plano, dos rectas son paralelas cuando no se cortan. Es decir, cuando no tienen puntos en común.
Ejemplo:
Las rectas \(y = 2x +1\) e \(y = 2x + 3\) son paralelas porque no se cortan:
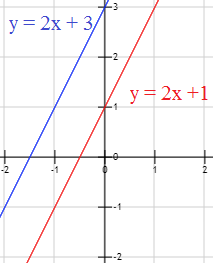
-
Las rectas \(y = x +2\) e \(y = 4x-1\) no son paralelas porque se cortan en el punto \(P = (1, 3)\):
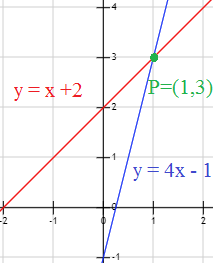
En efecto, las coordenadas de este punto cumplen ambas ecuaciones:
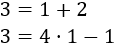
Definición 2:
Dos rectas son paralelas si tienen la misma pendiente (coeficiente \(a\)).
4. Rectas perpendiculares
Definición 1:
Dos rectas son perpendiculares si se cortan formando un ángulo recto (un ángulo de 90 grados).
Ejemplo:
Las rectas \( y = x+2\) e \(y = -x+2\) son perpendiculares:
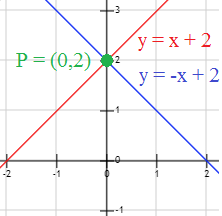
Dos rectas perpendiculares se cortan en un único punto.
Definición 2:
Las rectas perpendiculares a la recta \( y = ax+b\) son las que tienen la pendiente \( -\frac{1}{a} \). Es decir, son las rectas
$$ y = -\frac{1}{a}\cdot x + k $$
Según el valor de la ordenada \(k\), las rectas se cortan en uno u otro punto.
5. Problemas Resueltos
Nota: en ocasiones utilizaremos el símbolo \(\bot\) para denotar perpendicularidad.
Problema 1
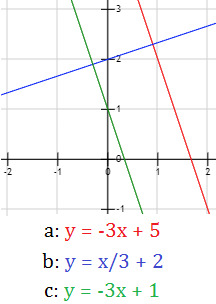
Representar las rectas \(a\), \(b\) y \(c\) y determinar si son paralelas (o perpendiculares) dos a dos.
\(a:\ y = -3x + 5\)
\(b:\ y = x/3 + 2\)
\(c:\ y = -3x + 1\)
Solución
La recta \(a\) y la recta \(c\) son paralelas porque tienen la misma pendiente.
La recta \(b\) es perpendicular a las rectas \(a\) y \(c\) porque tiene pendiente inversa y de signo contrario.
Problema 2
Encontrar cuatro rectas paralelas a la recta vertical \(x = 3\).
Solución
Las rectas verticales no tienen pendiente y todas ellas son paralelas. Algunas de estas rectas son:
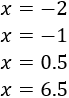
Las gráficas son
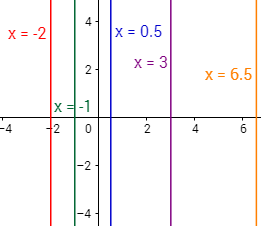
Problema 3
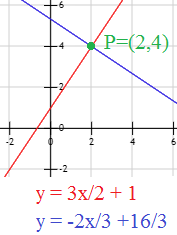
Encontrar el valor de \(B\) para que las rectas perpendiculares \(y = \frac{3x}{2}+1\) e \(y = -\frac{2x}{3}+B\) se corten en el punto \(P=(2,4)\).
Solución
Como el punto \(P\) está en las dos rectas, cumple ambas ecuaciones. En particular, cumple la segunda.
Sustituimos las coordenadas de \(P=(2,4)\) para hallar \(B\):
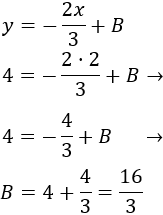
Representación:
Problema 4 (dificultad alta)
Encontrar la recta \(d\) para que las rectas \(a\), \(b\), \(c\) y \(d\) se corten formando un cuadrado:
\(a:\ y = x-4\)
\(b:\ y = x+2\)
\(c:\ y = -x-2\)
Solución
Las rectas \(a\) y \(b\) son paralelas y la recta \(c\) es perpendicular a ellas. La recta \(d\) que buscamos debe ser paralela a la recta \(c\). Por tanto, su ecuación será de la forma
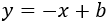
Como tienen que formar un cuadrado, debemos conseguir que todos los lados midan lo mismo.
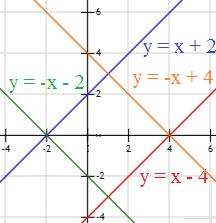
Representamos las tres rectas del enunciado:
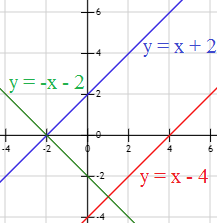
La recta \(a\) (rojo) es la recta \(b\) (azul) desplazada 6 unidades hacia abajo ya que
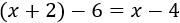
Para calcular la recta que buscamos, desplazamos la recta \(c\) (verde) 6 unidades hacia arriba:
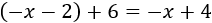
Por tanto, la recta \(d\) es
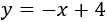
Representación:
Problema 5
Sin representar las siguientes rectas, determinar cuáles son paralelas y/o perpendiculares entre sí:
\(a:\ y =\frac{3x}{2} + 2\)
\(b:\ y = -\frac{3x}{2} + 2\)
\(c:\ y = \frac{2x}{3} + 1\)
\(d:\ y = \frac{2x}{3} + 5\)
\(e:\ y =\frac{3x+8}{2} \)
\(f:\ y =-\frac{2x+9}{3} \)
Solución
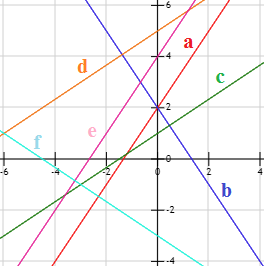
Las rectas \(a\) y \(e\) son paralelas (pendiente \(3/2\)).
Las rectas \(c\) y \(d\) son paralelas (pendiente \(2/3\)).
La recta \(b\) es perpendicular a las rectas \(c\) y \(d\).
La recta \(f\) es perpendicular a las rectas \(a\) y \(e\).
Representamos las rectas:
Problema 6
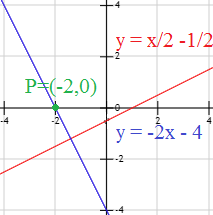
Hallar la recta que pasa por el punto \(P=(-2,0)\) y que es perpendicular a la recta
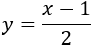
Solución
La ecuación en su forma general es
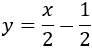
Así que su pendiente es \(m = 1/2\).
Por tanto, la ecuación de la recta perpendicular debe ser de la forma
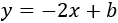
Para calcular \(b\), sustituimos las coordenadas del punto \(P=(-2,0)\) en la ecuación:
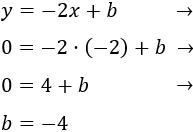
La recta buscada es \(y = -2x-4\).
Problema 7
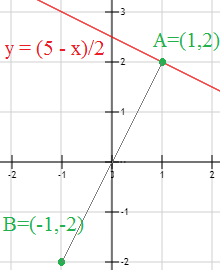
Si \(A=(1,2)\) y \(B=(-1,-2)\), encontrar la recta que pasa por \(A\) y es perpendicular a la recta que une a los puntos \(A\) y \(B\).
Solución
Podemos calcular la pendiente de la recta que pasa por \(A\) y \(B\) aplicando la fórmula
$$ m = \frac{y_2-y_1}{x_2-x_1} $$
La pendiente es
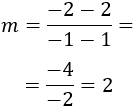
Por tanto, la pendiente de la recta perpendicular debe ser
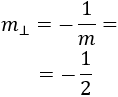
La ecuación de la recta será de la forma
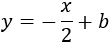
Calculamos \(b\) sustituyendo las coordenadas del punto \(A=(1,2)\) porque éste debe estar en la recta:
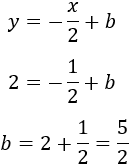
La recta buscada es
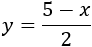
Representación:
Problema 8
Encontrar la recta que pasa por el punto \(P=(2,0)\) y que es perpendicular a la recta horizontal \(y = 4\).
Solución
Normalmente, la pendiente de la recta perpendicular es el inverso en signo contrario de la pendiente de la recta a la que debe ser perpendicular. Sin embargo, las pendiente de una recta horizontal es 0 y, por tanto, no podemos escribir su inverso.
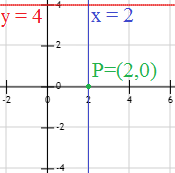
Las rectas perpendiculares a las rectas horizontales son las rectas verticales. Como la recta debe pasar por el punto \(P = (2,0)\), la recta buscada es \(x=2\).
Representación:
Problema 9 (dificultad alta)
Distancia entre dos paralelas
Si \(a\) y \(b\) son dos rectas paralelas, nunca se cortan. Si se traza una recta perpendicular a las dos rectas paralelas, \(c\), la distancia entre las paralelas es la distancia que hay entre los puntos en los que \(c\) corta a las paralelas.
Nota: si las rectas no son paralelas, la distancia que hay entre ellas es 0 ya que se cortan en algún punto.
Nota 2: la distancia entre dos puntos \((x_1, y_1)\) y \((x_2,y_2)\) viene dada por
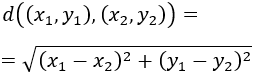
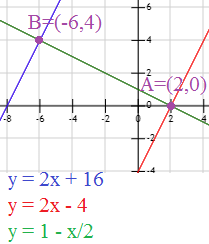
Encontrar la distancia entre las rectas paralelas \(a\) y \(b\):
\( a:\ y = 2x-4\)
\( b:\ y = 2x+16\)
Solución
Como la pendiente de las rectas \(a\) y \(b\) es \(m = 2\), la pendiente de las rectas que son perpendiculares a ellas es
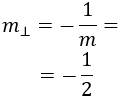
Una recta perpendicular a \(a\) y a \(b\) es, por ejemplo,
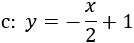
Buscamos los puntos de corte igualando las ecuaciones.
Punto de corte de \(c\) con \(a\):
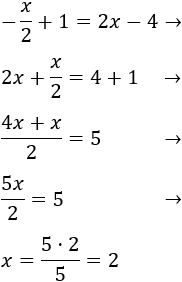
La segunda coordenada es
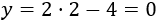
El punto de corte es \(A=(2,0)\).
Punto de corte de \(c\) con \(b\):
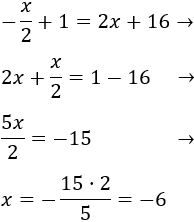
La segunda coordenada es
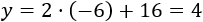
El punto de corte es \(B = (-6,4)\).
Finalmente, calculamos la distancia entre los puntos \(A\) y \(B\):
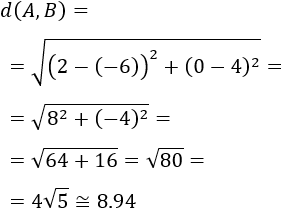
La distancia entre las rectas es de 8.94, aproximadamente.
Problema 10
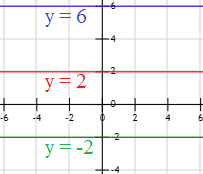
Encontrar la recta \(b\) para que la distancia entre las rectas \(a\) y \(b\) sea igual a 4.
\( a:\ y = 2\)
Solución
La recta \(b\) debe ser paralela porque, si no, la distancia entre ellas sería 0 (porque se cortan en algún punto).
Como la recta \(a\) es horizontal, \(b\) también tiene que serlo.
Es fácil deducir que la recta \(b\) puede ser \(y = 6\) ó bien \(y = -2\).
Problema 11
Utilizando la fórmula dada para calcular la pendiente,
$$ m = \frac{y_2-y_1}{x_2-x_1} $$
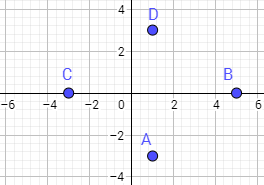
Comprobar si la recta que une a los puntos \(A = (1,-3)\) y \(B=(5,0)\) y la recta que une a \(C=(-3,0)\) y \(D=(1,3)\) son rectas paralelas.
Solución
Como dos rectas son paralelas si tienen la misma pendiente, vamos a calcular la pendiente de ambas rectas aplicando la fórmula dada en el enunciado.
Pendiente para los puntos \(A = (1,-3)\) y \(B=(5,0)\):
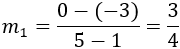
Pendiente para los puntos \(C=(-3,0)\) y \(D=(1,3)\):
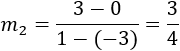
Como las pendientes son iguales, las rectas son paralelas.
Problema 12
Encontrar la recta que pasa por el punto \(P=(0,2)\) y que es perpendicular a la recta
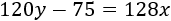
Solución
Lo primero que hacemos es escribir la ecuación en su forma normal. Para ello, dividimos la ecuación entre 120 y aislamos la \(y\):
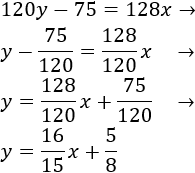
Así, podemos identificar la pendiente:
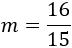
Las rectas perpendiculares a la recta con pendiente \(m\) tienen pendiente
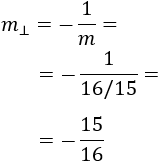
Luego la ecuación de la recta perpendicular es de la forma
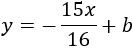
Como el punto \( P=(0,2)\) está en la recta que buscamos, sustituimos sus coordenadas en la ecuación para hallar la ordenada \(b\):
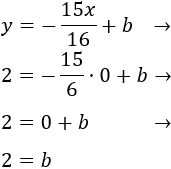
Por consiguiente, la recta perpendicular buscada es
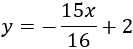
Representación:
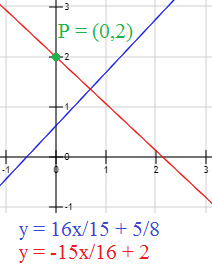
Problema 13
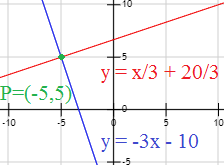
Calcular el punto en el que se cortan las rectas perpendiculares \(a\) y \(b\):
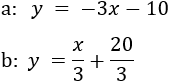
Solución
Para calcular la intersección de dos rectas, igualamos sus expresiones y resolvemos la ecuación obtenida:
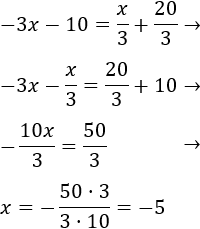
La primera coordenada del punto intersección es \(x = -5\). Calculamos la segunda coordenada:
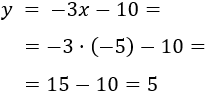
El punto es \(P=(-5,5)\).
Problema 14
Encontrar la ecuación que pasa por el punto \(P=(-4,4)\) y que es paralela a la recta
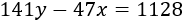
Solución
Despejamos \(y\) para escribir la ecuación en su forma normal porque si no tiene esta forma, la pendiente no es el coeficiente de la \(x\). Para ello, dividiremos entre 141:
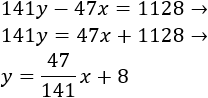
Luego la pendiente de la recta es
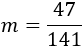
La fracción anterior no es irreductible y se puede simplificar más:
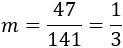
Buscamos una recta paralela, así que su ecuación es de la forma
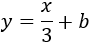
Sustituimos las coordenadas del punto \(P=(-4,4)\) en la ecuación para hallar la ordenada \(b\) y que la recta pase por \(P\):
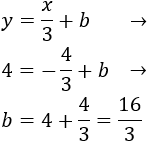
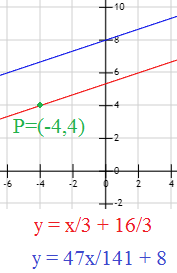
Por lo tanto, la ecuación de la recta paralela buscada es
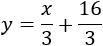
O bien,
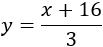
Representación:
Problema 15
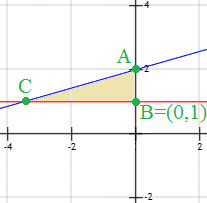
La recta de color azul es la gráfica de la ecuación
$$ g(x) = \frac{2}{7}x+2$$
Calcular:
-
La función \(f(x)\) cuya gráfica es la recta de color rojo.
-
El punto de intersección de ambas rectas (punto \(C\) ).
-
El ángulo que forma la recta de color azul con la recta de color rojo.
-
El área del triángulo cuyos vértices son los puntos \(A\), \(B\) y \(C\).
Ayuda: aunque no es necesario para resolver el problema, el ángulo \(\alpha\) que forman las rectas con pendiente \(m_1\) y \(m_2\) cumple
$$ tg(\alpha ) = \frac{m_2-m_1}{1+m_1\cdot m_2}$$
Solución
Apartado a:
La recta de color rojo es horizontal y pasa por el punto \(B=(0,1)\). Por tanto, su ecuación es \( y = 1\). Luego es la gráfica de la función \(f\) es \(f(x) = 1\).
Apartado b:
Para calcular el punto de intersección de dos funciones, igualamos sus expresiones:
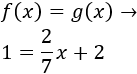
Resolvemos la ecuación de primer grado:
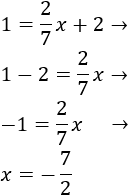
Por tanto, la primera coordenada del punto \(C\) es \(x = -7/2\). La segunda es \(y=1\) ya que el punto está en la recta horizontal. Luego \(C = (-7/2,1)\).
Apartado c:
Para calcular el ángulo, tenemos dos opciones:
Calcularemos el ángulo de ambas formas. Para aplicar la fórmula, necesitamos las pendientes de las rectas.
La pendiente de la recta de color azul es \(m=2/7\) y la de la recta de color rojo es \(m = 0\) (porque la recta es horizontal: \( y = 0\cdot x + 1\).
Por tanto,
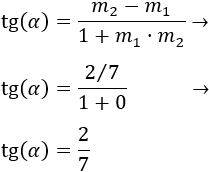
Luego el ángulo es
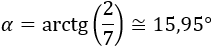
Ahora calculamos el ángulo sin aplicar la fórmula:
Como conocemos las coordenadas de todos los puntos, el triángulo con vértices \(A\), \(B\) y \(C\) es rectángulo y sus catetos miden 1 y 7/2 (altura y base).
Por el teorema de Pitágoras, podemos calcular la hipotenusa:
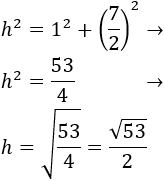
Sabiendo la medida de los catetos y de la hipotenusa, podemos calcular el ángulo por trigonometría básica.
Utilizamos el seno, que es cateto opuesto dividido entre la hipotenusa:
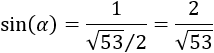
Por tanto, el ángulo \(\alpha\) que forman las rectas es
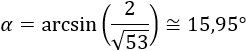
Apartado d:
Finalmente, calculamos el área del triángulo sabiendo que su altura mide 1 y su base mide 7/2:
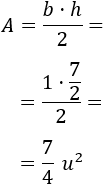
Nota: como no se proporcionan las unidades de medida, escribimos \(u^2\), cuyo significado es unidades al cuadrado.
Problema 16
Un arquitecto debe construir una valla que une a los puntos \(A = (3,7)\), \(B=(4,-4)\), \(C=(-5,-1)\) y \(D=(-3,5)\).
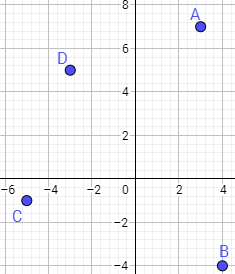
Contestar:
-
¿Cuál es la longitud total de la valla (en unidades de metro)?
-
¿Alguno de los segmentos que conforman la valla son paralelos o perpendiculares?
Solución
Primero representamos los segmentos que unen a los puntos:
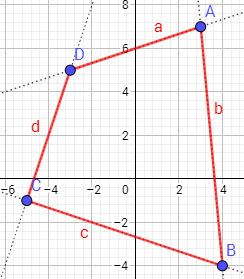
Apartado b:
Observando la representación, ya sabemos que ninguno de los cuatro segmentos son paralelos ya que si los alargamos, se cortan en algún punto. También, que los únicos segmentos que podrían ser perpendiculares son el \(d\) y el \(c\). Los otros no lo son claramente.
Para saber si los segmentos \(d\) y \(c\) son perpendiculares, vamos a calcular sus pendientes aplicando la fórmula que hemos utilizado en el Problema 11:
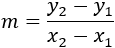
Para los puntos \(C=(-5,-1)\) y \(D=(-3,5)\),
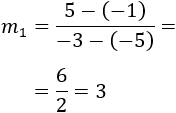
Para los puntos \(B=(4,-4)\) y \(C=(-5,-1)\),
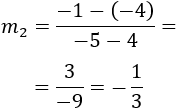
Por tanto, tenemos que las pendientes son inversas y de signo contrario, es decir,
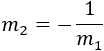
Así que los segmentos \(d\) y \(c\) sí son perpendiculares.
Apartado a:
Tenemos que sumar las longitudes de los cuatro segmentos.
Observemos que, por ejemplo, la longitud del segmento \(a\) es igual a la distancia que hay entre sus extremos (puntos \(A\) y \(D\)). Por consiguiente, es suficiente con calcular cuatro distancias.
Recordamos que la distancia entre dos puntos \((x_1, y_1)\) y \((x_2,y_2)\) viene dada por
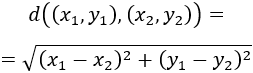
Calculamos la distancia entre los puntos \(A = (3,7)\) y \(D=(-3,5)\):
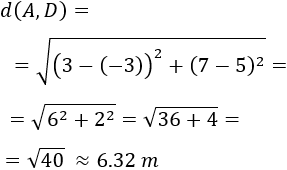
Distancia entre los puntos \(A = (3,7)\) y \(B=(4,-4)\):
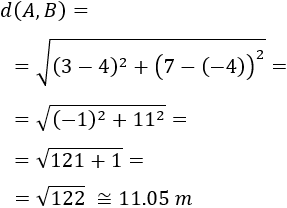
Distancia entre los puntos \(B=(4,-4)\) y \(C=(-5,-1)\):
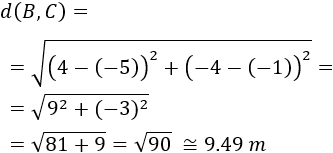
Distancia entre los puntos \(C=(-5,-1)\) y \(D=(-3,5)\):
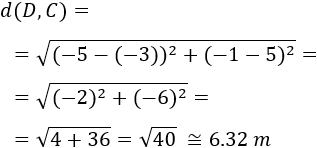
Sumamos las cuatro longitudes:
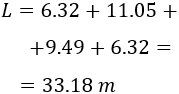
Luego la valla mide, aproximadamente, 33.18 metros de longitud.
Problema 17
La ecuación de la recta \(a\) es
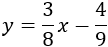
Calcular:
-
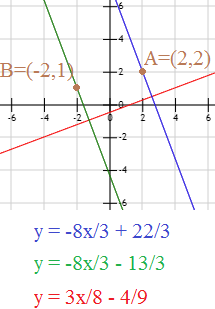
La recta \(b\) que pasa por el punto \(A=(2,2)\) y es perpendicular a la recta \(a\).
-
La recta \(c\) que pasa por el punto \(B=(-2,1)\) y es perpendicular a la recta \(a\).
Las rectas \(b\) y \(c\) son perpendiculares a la recta \(a\), pero ¿son paralelas o perpendiculares entre ellas?
Solución
Apartados a y b:
Para calcular las rectas perpendiculares a la recta \(a\), necesitamos su pendiente. De la ecuación, sabemos que es \(m = 3/8\).
Por tanto, la pendiente de ambas rectas perpendiculares debe ser
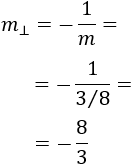
Luego la ambas ecuaciones serán de la forma
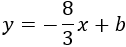
Sustituimos las coordenadas de \(A=(2,2)\) en la ecuación para encontrar la ordenada \(b\):
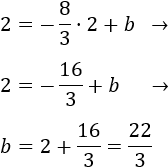
Ahora sustituimos las coordenadas de \(B=(-2,1)\):
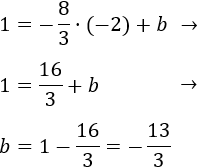
Por tanto, la recta perpendicular a \(a\) y que pasa por \(A\) es
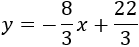
Y la recta perpendicular a \(a\) y que pasa por \(B\) es
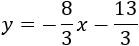
Ambas rectas tienen la misma pendiente, así que son paralelas entre ellas.
Problema 18 (problema teórico)
En la sección “Recordatorio” hemos dicho que la pendiente de la recta que une a los puntos \(A = (x_1,y_1)\) y \(B=(x_2,y_2)\) es
$$ m = \frac{y_2-y_1}{x_2-x_1} $$
Justificar la fórmula.
Ayuda: suponer que ambos puntos pertenecen a la recta \(y = mx+n\) .
Solución
Sea \(y = mx+n\) la recta que une a los puntos \(A\) y \(B\). La pendiente de la recta es \(m\). Como los puntos \(A\) y \(B\) están en la recta, sus coordenadas deben cumplir la ecuación. Por tanto, las coordenadas de los puntos deben cumplir la ecuación.
Sustituyendo en la ecuación obtenemos dos ecuaciones:
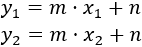
Ahora, restamos la primera ecuación a la segunda:
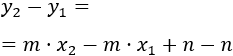
Simplificamos:
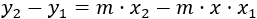
Extraemos factor común de \(m\):
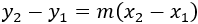
Aislamos la pendiente \(m\) en la ecuación:
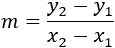
Problema 19
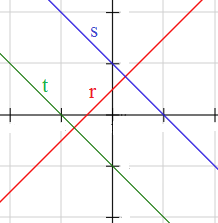
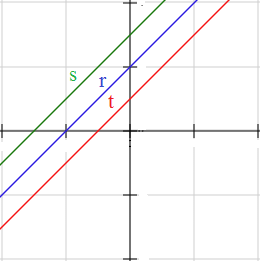
¿La propiedad de paralelismo de las rectas es una propiedad transitiva? Es decir, si las rectas \(r\) y \(s\) son paralelas y las rectas \(r\) y \(t\) son paralelas, entonces ¿las rectas \(s\) y \(t\) son también paralelas?
Solución
Sí, la propiedad de paralelismo es transitiva.
Si las rectas \(r\) y \(s\) son paralelas, es porque tienen la misma pendiente.
Lo mismo ocurre con las pendientes de \(r\) y \(t\).
Como consecuencia, las pendientes de \(s\) y \(t\) también coinciden.
Problema 20
¿La propiedad de perpendicularidad de las rectas una propiedad transitiva?
Solución
No, la propiedad de perpendicularidad no es transitiva.
Supongamos que las rectas \(r\) y \(s\) son perpendiculares y que las rectas \(r\) y \(t\) también son perpendiculares.
Si la pendiente de \(r\) es \(m\), entonces la pendiente de \(s\) y de \(t\) es \(-1/m\). Por tanto, las rectas \(s\) y \(t\) tienen la misma pendiente, con lo que son paralelas entre ellas, pero no perpendiculares.