Contenido de esta página:
Introducción: triángulo rectángulo, seno, coseno, tangente, arcoseno y arcocoseno.
15 problemas resueltos (seno y coseno).
Páginas relacionadas:
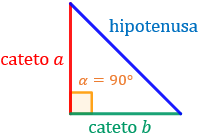
Recordatorio: triángulo rectángulo, catetos, hipotenusa, ángulo recto y referencia al teorema de Pitágoras.
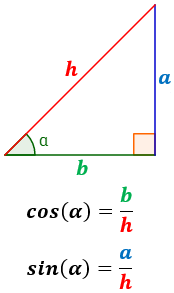
Definición del seno y del coseno del ángulo como el cociente de los lados del triángulo y regla mnemotécnica.
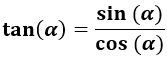
Definición de la tangente.
Nota: no utilizaremos la tangente para resolver los problemas de esta página, aunque es una opción.
Qué son y para qué sirven las funciones arcoseno y arcocoseno y algunas consideraciones.
Nota previa: para simplificar los cálculos, aproximaremos las razones trigonométricas con dos, tres o cuatro decimales por redondeo o por truncamiento. Como consecuencia, los resultados pueden ser no exactos.

Se desea sujetar un poste de 20 metros de altura con un cable que parte de la parte superior del mismo hasta el suelo de modo que forme un ángulo de 30º con el suelo para cumplir con la normativa de seguridad:
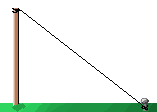
Calcular el precio del cable si cada metro cuesta 12$. ¿Cuál es el ángulo que forma el cable con el poste?
El cateto verde de la representación es el poste, la hipotenusa (azul) es el cable y el cateto marrón es el suelo. El cable forma un ángulo de 30º con el suelo:
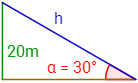
Debemos calcular primero la longitud del cable que necesitamos (por trigonometría) para poder calcular su precio.
Debemos elegir entre utilizar el seno o el coseno:
Como conocemos el lado opuesto del ángulo, \(a=20m\), utilizamos el seno para calcular la hipotenusa del triángulo, que es el cable que sujetará el poste:
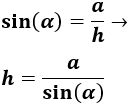
Sustituimos el ángulo y el lado:
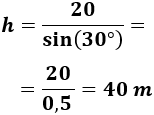
Luego el cable debe medir 40 metros y su precio es de 480$:
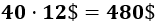
Nota: observad que no nos serviría el coseno porque éste es el lado contiguo (suelo) entre la hipotenusa (cable).
Finalmente, como la suma de los ángulos de un triángulo debe ser 180 grados y el triángulo del problema tiene un ángulo de 30º y otro de 90º, el otra ángulo es de 60 grados (entre el cable y el poste).

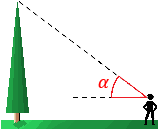
Calcular la altura, \(a\), de un árbol sabiendo que, si nos situamos 8 metros de la base del tronco, vemos la parte superior de su copa en un ángulo \(\alpha = 36.87^\circ \) (los ojos a nivel del suelo).
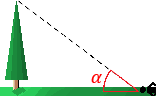
¿Cuál sería la altura del árbol si consideramos que estamos de pie y los ojos situados a 170 cm del suelo en lugar de a nivel del suelo?
Primera parte:
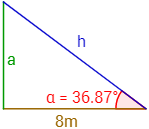
Como la altura \(a\) es el cateto opuesto al ángulo, utilizaremos el seno (y no el coseno):
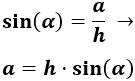
Ahora bien, conocemos el seno del ángulo pero necesitamos calcular la hipotenusa \(h\) del triángulo.
Usamos el coseno:
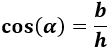
Sustituimos los datos:
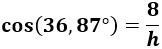
La hipotenusa mide
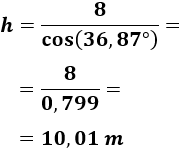
Ahora ya podemos usar el seno para calcular la altura del árbol:
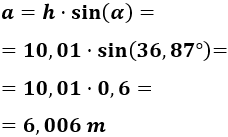
Nota: otra forma más rápida es usar la tangente, que es el seno entre el coseno (lado opuesto entre lado contiguo):
$$ \tan(36.87^\circ) = \frac{a}{8}$$
De donde obtenemos la altura \(a\):
$$ a = 8\cdot \tan(36.87^\circ) \simeq 6,000 \text{ m}$$
Segunda parte:
La situación del problema cambia un poco:
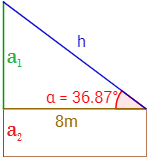
Observad que la altura del árbol es \(a_1+a_2\), siendo \(a_2\) la altura a la que se sitúan los ojos (1,7 metros), los cuales se encuentran en el vértice del triángulo cuyo ángulo es \(\alpha\).
Las operaciones anteriores nos sirven, sólo tenemos que sumar 1,7 a la altura del árbol. Luego el árbol mediría 7,7 metros.
Nota: hemos considerado que el ángulo \(\alpha\) es la amplitud del ángulo de movimiento de los ojos desde una vista paralela al suelo (y no desde el suelo).

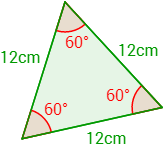
Calcular cuánto mide la mediana de un triángulo equilátero (los tres ángulos son de 60 grados) cuyos lados miden 12cm.
Ayuda: la mediana es la longitud del segmento que une un vértice del triángulo con el punto medio del lado opuesto a éste.
La mediana forma un triángulo rectángulo:
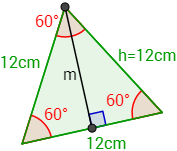
Tenemos que calcular uno de los dos catetos del triángulo rectángulo: \(m\). Podemos utilizar el seno porque \(m\) es el lado opuesto al ángulo de 60º y la hipotenusa mide 12cm:
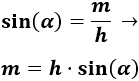
Sustituimos los datos:
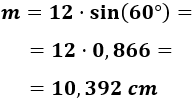
Luego la mediana mide 10,392 centímetros.
Nota: este problema también se puede resolver aplicando el teorema de Pitágoras porque sabemos que la hipotenusa mide 12cm y uno de los catetos mide 6cm (es la mitad del lado del triángulo equilátero):
$$ 12^2 = m^2 + 6^2$$
$$m = \sqrt{12^2 - 6^2} \simeq 10,392 \text{ cm}$$

Escribir una fórmula para calcular la longitud de la mediana de un triángulo equilátero de lado \(d\).
Usando dicha fórmula, ¿cúanto mide la mediana de un triángulo equilátero de lado 2 metros?.
Ayuda: la fórmula se puede obtener rápidamente a partir del problema anterior.
Como los lados del triángulo miden \(d\) en lugar de 12cm, sólo tenemos que cambiar 12 por \(d\) en el problema anterior ya que los ángulos son iguales.
La fórmula es
$$ \text{mediana} = d\cdot \sin(60^\circ)$$
O bien, como \(\sin(60^\circ) = \sqrt{3}/2\),
$$ \text{mediana} = d\cdot \frac{\sqrt{3}}{2}$$
Nota: si se ha usado Pitágoras en el problema anterior, entonces tendremos
$$ \text{mediana} = \sqrt{d^2 - (d/2)^2} =$$
$$ = \sqrt{\frac{3d^2}{4}} = d\cdot \frac{\sqrt{3}}{2}$$
Aplicamos la fórmula para calcular la mediana de un triángulo equilátero de lado \(d = 2\text{ m}\):
$$ \text{mediana} = d\cdot \frac{\sqrt{3}}{2} =$$
$$ = 2\cdot \frac{\sqrt{3}}{2} = \sqrt{3}\text{ m}$$
Si aproximamos, la mediana mide 1,7321 metros.

Del siguiente triángulo rectángulo se conocen sus dos catetos: uno mide 4m y el otro mide 3m.
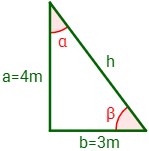
Calcular la hipotenusa \(h\) y los ángulos \(\alpha\) y \(\beta\).
Como el triángulo es rectángulo, aplicamos el teorema de Pitágoras para calcular la hipotenusa:
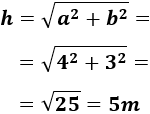
La hipotenusa mide 5 metros.
Para calcular los ángulos podemos utilizar, por ejemplo, el seno:
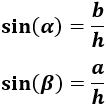
Nota: el seno es el lado opuesto al ángulo entre la hipotenusa. Obviamente, debemos tener cuidado al localizar el lado opuesto de cada ángulo.
Como conocemos los catetos (\(a\) y \(b\)) y la hipotenusa (\(h\)), podemos calcular el seno de los ángulos:
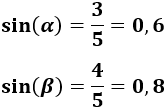
Finalmente, para calcular los ángulos sólo debemos utilizar la función arcoseno (inversa del seno, \(\sin^{-1}\)):

Nota: el arcoseno en la calculadora suele ser tecla shift + tecla sin.

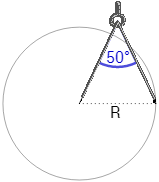
Calcular el radio de la circunferencia que se obtiene al utilizar un compás cuyos brazos miden 10cm si éstos forman un ángulo de 50º entre sí.
Representamos los ángulos que forman los brazos con el papel y escribimos los datos que tenemos:
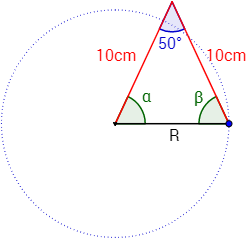
El compás junto con el radio \(R\) forma un triángulo isósceles (dos lados iguales). Esto significa que los ángulos \(\alpha\) y \(\beta\) son iguales.
Como la suma de los ángulos (interiores) de un triángulo es siempre 180º, podemos calcular \(\alpha = \beta\):
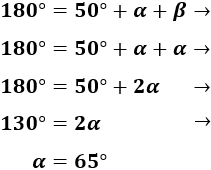
Al representar la altura \(h\), tenemos dos triángulos rectángulos iguales de hipotenusa 10cm, un cateto \(h\) y otro cateto \(R/2\):
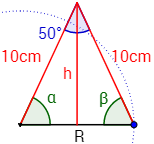
Si llamamos \(b = R/2\) a la mitad del radio y aplicamos el coseno, tenemos
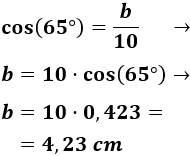
Por tanto, el radio de la circunferencia mide 8,46cm:
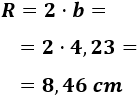
Nota: también podríamos haber usado el seno y el ángulo de 50º, pero observad que el ángulo queda reducido a la mitad al representar la altura del triángulo:
$$ R = 2\cdot b = 2\cdot 10\cdot \sin(25^\circ) \simeq 8.46\text{ cm}$$

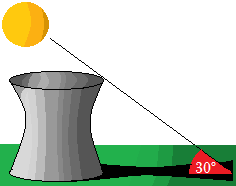
Calcular la altura de la torre de refrigeración de una central nuclear si se sabe que su sombra mide 271 metros de longitud desde la base de la torre cuando los rayos solares inciden formando un ángulo de 30º.
Llamamos \(a\) a la altura y \(h\) a la hipotenusa. Aplicando el seno,
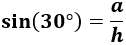
Despejamos la altura:
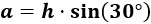
Necesitamos la hipotenusa, pero podemos obtenerla usando el coseno:
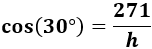
Despejamos la hipotenusa:
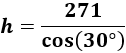
Sustituimos la hipotenusa:
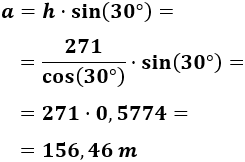
Por tanto, la altura de la torre es de unos 156,46 metros.
Nota: si hubiésemos optado por la tangente, tendríamos
$$ \tan(30^\circ ) = \frac{a}{271} $$
$$ a = 271\cdot \tan(30^\circ ) \simeq 156.46 \text{ m}$$

De acuerdo con el GPS, las ciudades A, B y C son los vértices de un triángulo rectángulo. Calcular la distancia entre las ciudades A y C y entre las ciudades B y C sabiendo que
La situación de las ciudades es la siguiente:
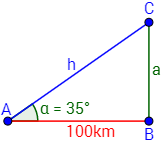
Por el seno y por el coseno tenemos las siguientes relaciones:
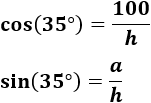
Calculamos la hipotenusa a partir del coseno:
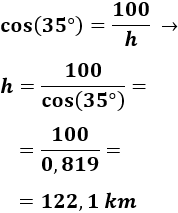
Conociendo la hipotenusa, calculamos \(a\) a partir del seno:
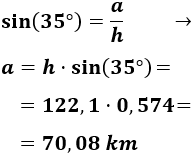
Por tanto, la distancia entre las ciudades A y C es de 122,1 kilómetros y la distancia entre las ciudades B y C es de 70,08 kilómetros.

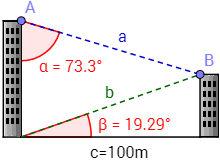
Miguel desea calcular la altura de dos edificios que están situados a 100 metros el uno del otro. Como tiene acceso al edificio más alto, observa que desde la azotea de dicho edificio (punto A) se avista la azotea del otro (punto B) bajo un ángulo de \(\alpha=73,3^{\circ}\). Desde la base del mismo edificio, se ve la azotea del otro edificio bajo un ángulo de \(\beta=19,29^{\circ}\).
¿Puede Miguel calcular la altura de los edificios con los tres datos con los que cuenta? En caso afirmativo, ¿cuál es la altura de cada uno?
Sí es posible calcular la altura de ambos edificios.
El ángulo \(\beta\) forma parte de un triángulo rectángulo. Representamos el segmento \(d\) horizontal para formar un triángulo rectángulo con el ángulo \(\alpha\):
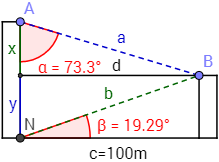
Obsérvese que el segmento \(d\) mide 100 metros, que la altura del edificio más alto es la suma de los catetos \(x\) e \(y\) y la altura del otro edificio es \(y\).
Por el seno y el coseno, tenemos las siguientes relaciones para el ángulo \(\alpha\):
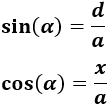
Como conocemos \(\alpha\) y \(d\), podemos calcular \(a\) y con ello podremos calcular \(x\). .
Primero, calculamos \(a\):
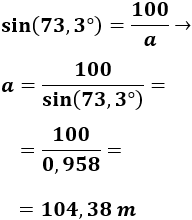
Ahora, calculamos \(x\):
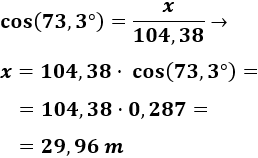
Por el seno y el coseno, tenemos las siguientes relaciones para el ángulo \(\beta\):
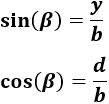
Como conocemos \(\beta\) y \(d\), podemos calcular \(b\) e \(y\).
Primero, calculamos \(b\):
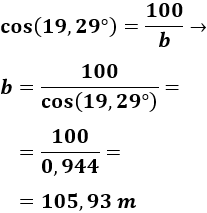
Ahora, calculamos \(y\):
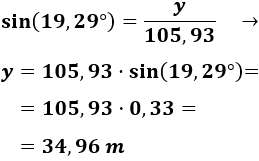
Ahora que ya tenemos \(x\) e \(y\) podemos calcular la altura del edificio alto, que es
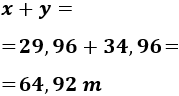
Y la altura del otro edificio es \(y\), esto es, 34,96 metros.

Desde una determinada distancia, una bandera situada en la parte superior de un torreón se observa con un ángulo de 47º. Si nos acercamos 17,8 metros al torreón, la bandera se observa con un ángulo de 75º.
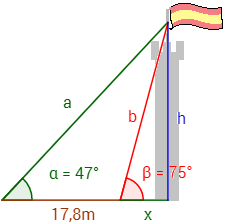
Calcular la altura a la que se encuentra la bandera.
Ayuda: se recomienda usar la tangente (seno entre coseno; lado opuesto entre lado contiguo).
Las relaciones que tenemos son
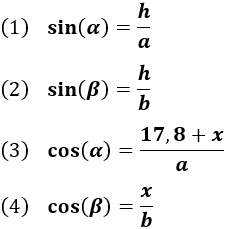
Escribimos la tangente de \(\alpha\):
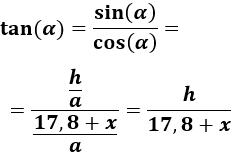
De donde podemos despejar \(x\):
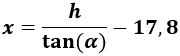
Escribimos la tangente de \(\beta\):
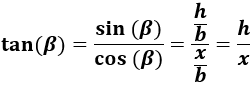
De donde despejamos la altura \(h\):
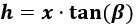
En la ecuación obtenida, sustituimos \(x\) por la expresión obtenida anteriormente:
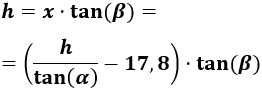
Resolvemos la ecuación:
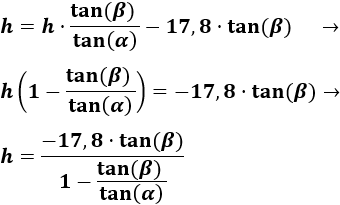
Nota: en la segunda línea se ha extraído factor común de \(h\) después de pasar \(h\cdot \frac{\tan(\beta )}{\tan(\alpha )}\) al lado izquierdo.
Finalmente, sustituimos los datos:

Por tanto, la bandera se encuentra a unos 26,78 metros de altura.

Se ha creado la siguiente figura uniendo dos triángulos:
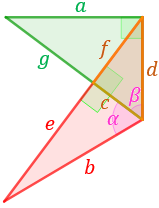
Calcular la longitud del lado \(a\) sabiendo que \(b = 4.7059\) centímetros, \(\alpha = 67.5113^\circ\) y \(\beta = 53.1301^\circ\).
Nos centramos en el triángulo rectángulo rojo, del que conocemos el lado \(b\) y el ángulo \(\alpha\). Podemos hallar el lado \(c\) mediante el coseno:
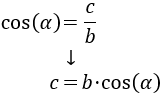
Sustituimos los datos:
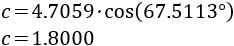
Nos centramos ahora en el triángulo rectángulo naranja, del que conocemos el lado \(c\) y el ángulo \(\beta\). Podemos hallar el lado \(d\) mediante el coseno:
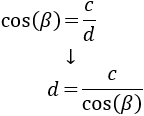
Sustituimos los datos:

Finalmente nos fijamos en el triángulo verde (el de lados \(a\), \(d\) y \(g+c\)), del que conocemos \(d\) y \(\beta\).
Usando el coseno podemos hallar \(g\):
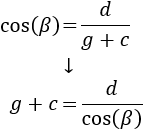
No sustituimos aún los datos.
Usando el seno podemos hallar \(a\):
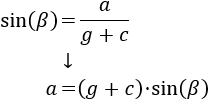
Sustituimos el \(g+c\) por el obtenido anteriormente:
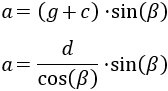
Sustituimos los datos:
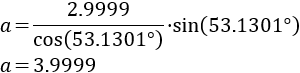
Por tanto, el lado \(a\) mide aproximadamente 3.99 centímetros.
Nota: en el paso anterior podríamos haber escrito la tangente:
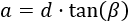

La siguiente fórmula se denomina identidad trigonométrica fundamental:
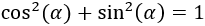
¿Sabrías demostrarla?
Ayuda: usar un triángulo rectángulo y el teorema de Pitágoras.
Consideremos un triángulo rectángulo de catetos \(a\) y \(b\) y ángulo no recto \(\alpha\):
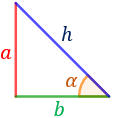
Sabemos, por Pitágoras, que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa:
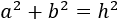
Escribimos el seno (coseno) del ángulo \(\alpha\) como el cociente del cateto opuesto (contiguo) y la hipotenusa:
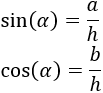
Calculamos sus cuadrados y los sumamos:
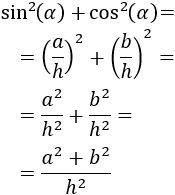
Recordad que hemos dicho anteriormente que \(a^2+b^2 = h^2\), con lo que
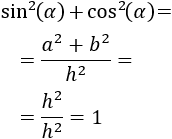

Determinar la longitud de los segmentos \(a\) y \(b\) de la siguiente figura obtenida a partir de una recta oblicua que corta una recta horizontal sabiendo que \(\alpha = 45^\circ\):
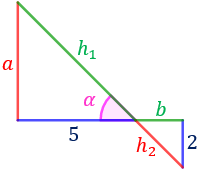
Ayuda: se puede usar el seno y el coseno, la tangente, o ninguno de ellos (sólo razonar).
Observad que ambos triángulos son rectángulos (tienen un ángulo recto).
El triángulo de la izquierda tiene, además, un ángulo de 45 grados. Esto implica que el otro ángulo sea también de 45 grados (porque la suma de los 3 ángulos debe ser 180 grados).
Luego el triángulo de la izquierda es un triángulo isósceles rectángulo: sus dos catetos miden lo mismo. Con lo que ya podemos afirmar que el lado \(a\) mide 5.
Por otro lado, tenemos el triángulo de la derecha, del que, en principio sólo sabemos que tiene un ángulo recto. Sin embargo, debemos recordar que dos rectas (o segmentos) que se cortan forman 4 ángulos iguales dos a dos, opuestos por el vértice:
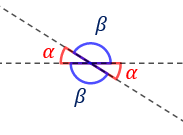
Por tanto, sabemos que el triángulo rectángulo también tiene un ángulo de 45 grados, además del recto y, por ende, otro ángulo de 45 grados. Se trata pues de otro triángulo isósceles rectángulo y sus dos catetos miden lo mismo: 2.
Luego \(a = 5\) y \(b = 2\).
También, podemos resolver el problema, por ejemplo, usando la tangente.
Triángulo de la izquierda:
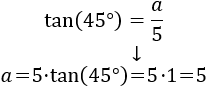
Triángulo de la derecha:
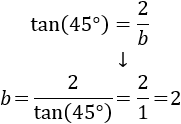

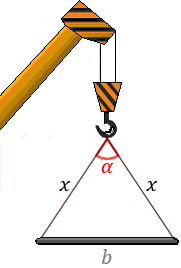
En la construcción de un edificio se está usando una grúa para mover vigas. La grúa tiene dos cadenas de longitud \(x\) que sujetan las vigas desde sus extremos forman un ángulo \(\alpha\) entre sí:
Responde:
Observad que el triángulo que forman las cadenas y la viga es isósceles (dos lados iguales y dos ángulos iguales).
Para poder aplicar el seno y el coseno necesitamos un triángulo rectángulo. Podemos construirlo con la altura del triángulo isósceles, la cual divide el ángulo y la viga por la mitad:
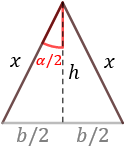
Escribimos el seno y el coseno del ángulo \(\alpha/2\):
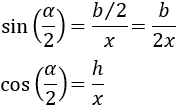
Con estas fórmulas podemos responder las tres preguntas.
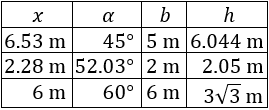
Primera pregunta: la viga mide 5 metros y las cadenas forman un ángulo \(\alpha = 45^\circ\).
Usamos el seno:
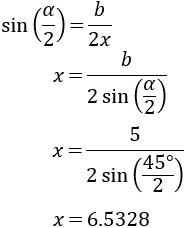
Las cadenas miden \(x = 6.5328\) metros.
Usamos el coseno:
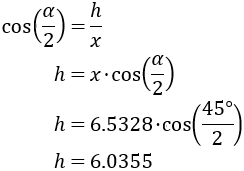
La distancia de la viga al garfio es de 6.0355 metros.
Segunda pregunta: la viga mide 2 metros y las cadenas miden 2.28 metros.
Usamos el seno:
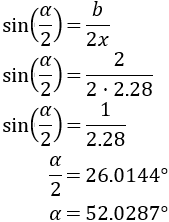
El ángulo es de 52.0287 grados.
Usamos el coseno:
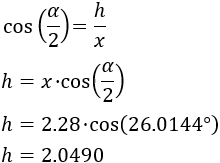
La distancia de la viga al garfio es de 2.049 metros.
Tercera pregunta: las cadenas miden 6 metros y forman un ángulo \(\alpha = 60^\circ\).
Usamos el seno:
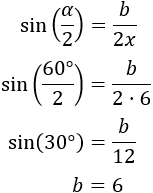
La viga mide 6 metros.
Usamos el coseno:
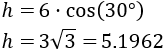
La distancia de la viga al garfio es de unos 5.1962 metros.
Tabla resumen:

En la parte superior de una pared de 3 metros de altura y 6 de ancho se colocan un foco de luz amarilla con ángulo de apertura \(\alpha\) y otro de luz roja con ángulo \(\beta\), de modo que los triángulos isósceles amarillo y rojo que proyectan los focos se solapan formando otro triángulo naranja con un ángulo \(\sigma\) :
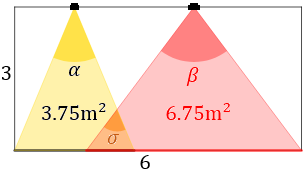
Determinar la amplitud de los ángulos \(\alpha\), \(\beta\) y \(\sigma\) sabiendo que el área del triángulo amarillo es de \(3.75\text{m}^2\) y el del triángulo rojo es de \(6.75\text{m}^2\).
Nota: las áreas de los triángulos no excluyen la del triángulo naranja (su área se cuenta en ambas áreas).
Llamemos \(x\) a la base del triángulo amarillo e \(y\) a la base del triángulo rojo. Tened en cuenta que como las bases se solapan, su suma no es el ancho de la pared:
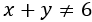
Ambos triángulos tienen altura 3 y conocemos su área (base por altura entre 2), así que podemos calcular \(x\) e \(y\).
Triángulo amarillo:
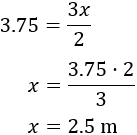
Triángulo rojo:
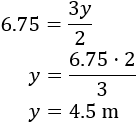
Luego las bases de los triángulos amarillo y rojo son 2.5 y 4.5 metros, respectivamente.
Representamos la altura de los triángulos amarillo y rojo (que es de 3 metros), para tener triángulos rectángulos:
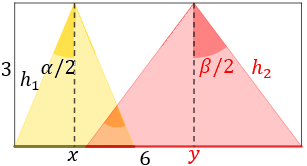
Nota: hemos llamado \(h_1\) y \(h_2\) a las hipotenusas.
Observando el triángulo amarillo, por el coseno tenemos:
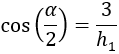
Para poder calcular \(\alpha\) necesitamos calcular la hipotenusa \(h_1\), lo cual es fácil aplicando Pitágoras:
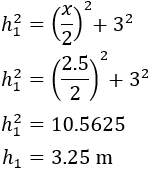
Ya podemos calcular \(\alpha\):
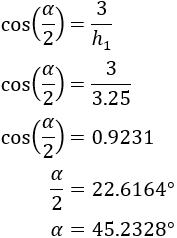
Repetimos el proceso con el triángulo rojo:
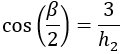
Calculamos la hipotenusa \(h_2\) por Pitágoras:
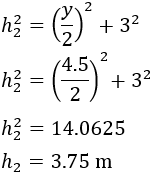
Ya podemos calcular \(\beta\):
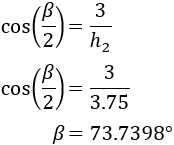
Nos falta calcular el ángulo \(\sigma\).
Observemos el triángulo naranja: no es rectángulo, ni es isósceles. Llamaremos \(\sigma_1\) y \(\sigma_2\) a los ángulos de la base derecho e izquierdo.
Los triángulos amarillo y rojo son isósceles. Entonces, los dos ángulos de la base son iguales:
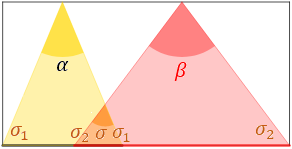
Observad que:
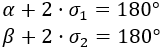
Por tanto, por un lado, tenemos:
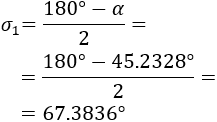
Por otro lado,
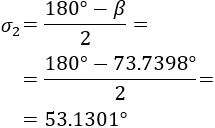
Finalmente, ya podemos calcular \(\sigma\):
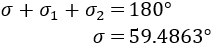
Por tanto, los ángulos son

Problemas resueltos de trigonometría para secundaria: seno y coseno - (c) - matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.