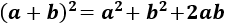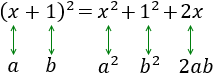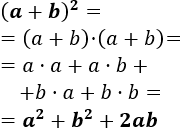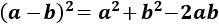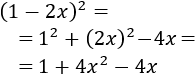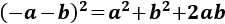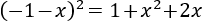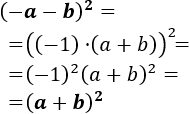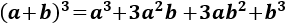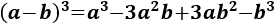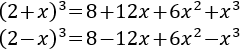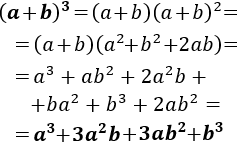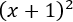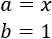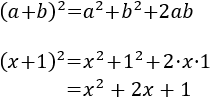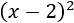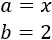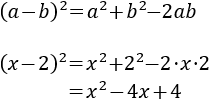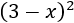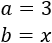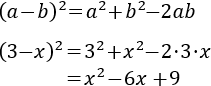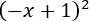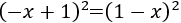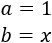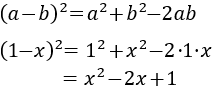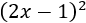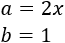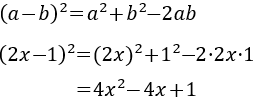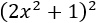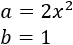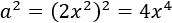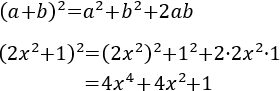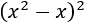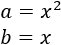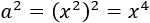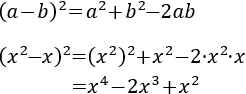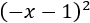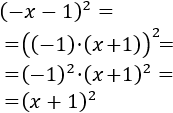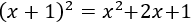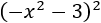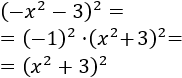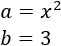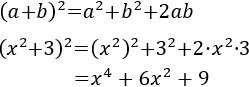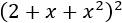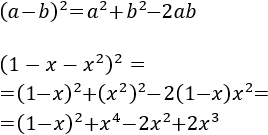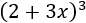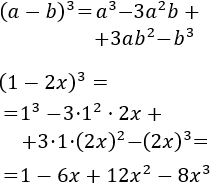Cuadrado y cubo de un binomio
En esta página proporcionamos las fórmulas para calcular el cuadrado y el cubo de una suma y de una resta. Con ejemplos, ejercicios resueltos y demostraciones.
Contenido de esta página:
- Introducción
- Cuadrado de la suma
- Cuadrado de la resta
- Cuadrado de dos sumandos negativos
- Cubo de la suma y de la resta
- Ejercicios resueltos
Páginas relacionadas
Otras páginas:
1. Introducción
Generalmente, nuestra intuición nos hace pensar que el cuadrado de la suma es la suma de los cuadrados, pero esto no es así. Por ejemplo, (1 + 1) 2 = 2 2 = 4, sin embargo, 12 + 12 = 2.
Se conoce como teorema del binomio de Newton a la fórmula que nos proporciona el resultado de la potencia de una suma, (a+b)k. Sólo vamos a proporcionar las fórmulas para el cuadrado (k=2) y el cubo (k=3), ya que la fórmula se complica a medida que aumenta el exponente k. También, calcularemos cuadrados de trinomios.