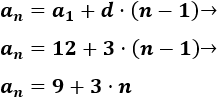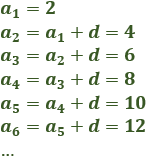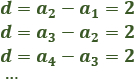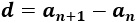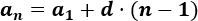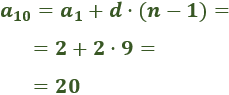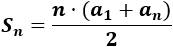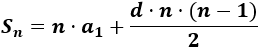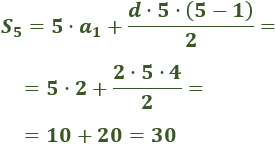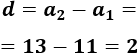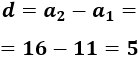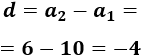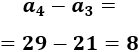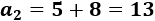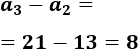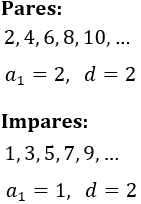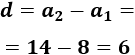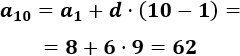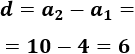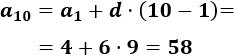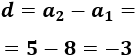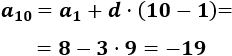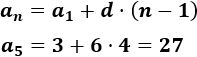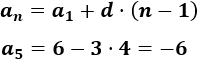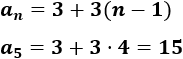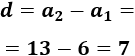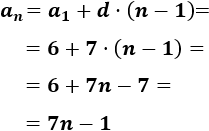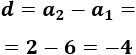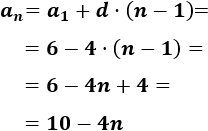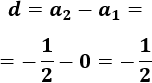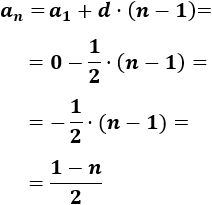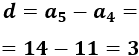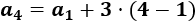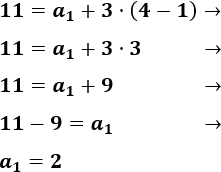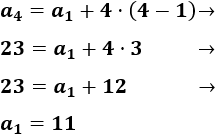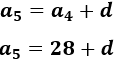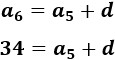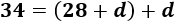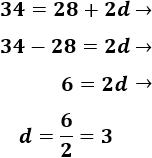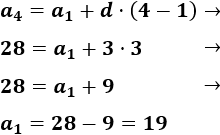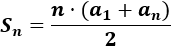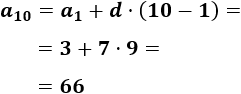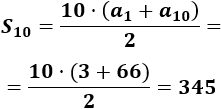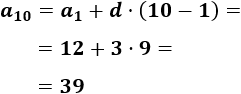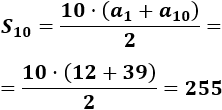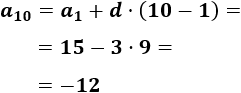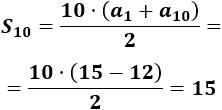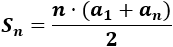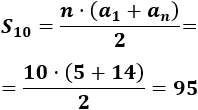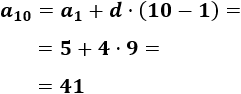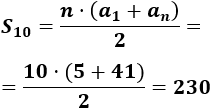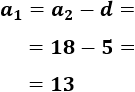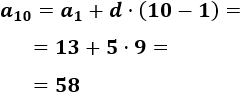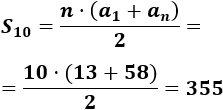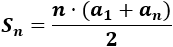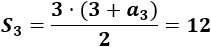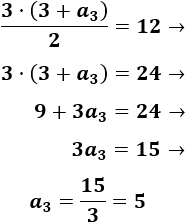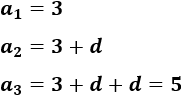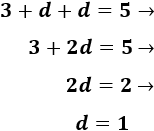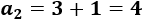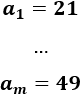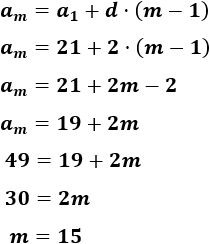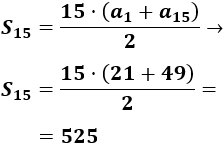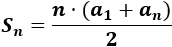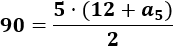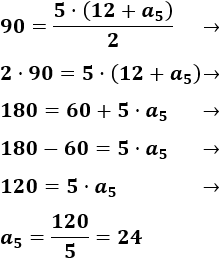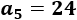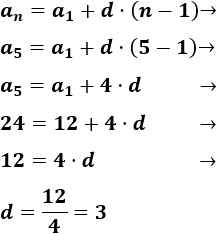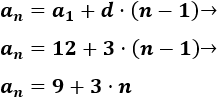Problema 1 
Calcular la diferencia de las siguientes sucesiones:
-
11, 13, 15, 17, 19,...
-
11, 16, 21, 26, 31,...
-
10, 6, 2, -2, -6, -10,...
Resolvemos:
Para calcular la diferencia tenemos que restar términos consecutivos. Restaremos el segundo y el primer término.
-
11, 13, 15, 17, 19, ...
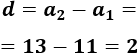
La diferencia es \(d = 2\).
-
11, 16, 21, 26, 31, ...
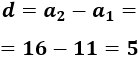
La diferencia es \(d = 5\).
-
10, 6, 2, -2, -6, -10, ...
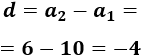
La diferencia es \(d = -4\).
Nota: Es aconsejable comprobar que la diferencia es constante en toda la sucesión (si esto no ocurre, la sucesión no es aritmética).
Problema 2 
¿Cuál de las siguientes sucesiones no es aritmética?
-
16, 26, 36, 46,...
-
16, 6, 13, 3,...
-
-26, -36, - 46, -56,...
Resolvemos:
La primera sucesión es aritmética con diferencia \(d = 10\).
La segunda sucesión no es aritmética porque la diferencia entre el segundo y el primer término es -10, mientras que la diferencia entre el tercero y el segundo es 7.
La tercera es aritmética con diferencia negativa: \(d = -10\).
Problema 3 
¿Cuál es el segundo término (\(a_2\)) de la siguiente sucesión aritmética?
$$ 5,a_2,21,29,... $$
Resolvemos:
Si sumamos la diferencia \(d\) al primer término, tendremos el segundo. Necesitamos calcular la diferencia y para ello sólo tenemos que restar términos consecutivos.
La diferencia entre el cuarto y el tercer término es
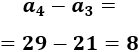
Calculamos \(a_2\) sumando la diferencia al primer término:
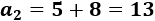
Comprobamos que la diferencia entre el tercer y el segundo término también es 8:
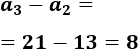
Problema 4 
Calcular los dos siguientes términos (\(a_4\) y \(a_5\)) de las siguientes sucesiones aritméticas:
-
45, 55, 65,...
-
11, 22, 33,...
-
87, 76, 65,...
¿Cuál es la diferencia de estas sucesiones?
Resolvemos:
Si calculamos las diferencias, fácilmente podremos calcular los términos siguientes.
-
45, 55, 65,...
La diferencia de la sucesión es 10. Por tanto, los dos siguientes términos son 75 y 85.
-
11, 22, 33,...
La diferencia de la sucesión es 11. Por tanto, los dos siguientes términos son 44 y 55.
-
87, 76, 65,...
La diferencia de la sucesión es -11. Por tanto, los dos siguientes términos son 54 y 43.
Problema 5 
Si dos sucesiones tienen la misma diferencia, ¿son la misma sucesión?
Resolvemos:
No. Si la diferencia es la misma pero el primer término es distinto, las sucesiones son diferentes. Por ejemplo, la sucesión de los pares y la de los impares tienen diferencia \(d=2\), pero son distintas:
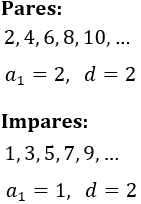
Problema 6 
Determinar si las siguientes sucesiones son crecientes o decrecientes:
-
20, 15, 10, 5,...
-
-3, -6, -9, -12,...
-
4, 14, 24, 34,...
Resolvemos:
-
20, 15, 10, 5,...
Decreciente (diferencia negativa \(d=-5 < 0\)).
20 > 15 > 10 > 5 > ...
-
-3, -6, -9, -12,...
Decreciente (diferencia negativa \(d=-3 < 0\)).
-3 > -6 > -9 > -12 > ...
-
4, 14, 24, 34,...
Creciente (diferencia positiva \(d=10 > 0\)).
4 < 14 < 24 < 34 < ...
Problema 7 
Calcular el décimo término (\(a_{10}\)) de cada sucesión:
-
8, 14, 20, 26,...
-
4, 10, 16, 22,...
-
8, 5, 2, -1,...
Resolvemos:
Calcularemos la diferencia para poder calcular el décimo término, pero usaremos el término general para no tener que calcular los términos intermedios. La fórmula que necesitamos es
$$ a_n = a_1 + d\cdot (n - 1) $$
-
8, 14, 20, 26,...
La diferencia es
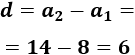
Por tanto, el término 10-ésimo es
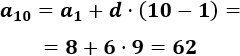
-
4, 10, 16, 22,...
La diferencia es
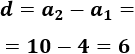
Por tanto, el término 10-ésimo es
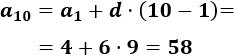
-
8, 5, 2, -1,...
La diferencia es
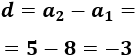
Por tanto, el término 10-ésimo es
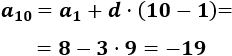
Problema 8 
Calcular el término \(a_5\) de cada sucesión a partir de los datos proporcionados:
-
\(a_1=3,\ d=6\)
-
\(a_1=6,\ d=-3\)
-
\(a_n=3+3(n-1)\)
Determinar si las sucesiones son crecientes o decrecientes.
Resolvemos:
En la primera y segunda sucesión conocemos el primer término y la diferencia, así que tenemos que usar la fórmula del término general (con \(n = 5\)):
$$ a_n = a_1 + d\cdot (n - 1) $$
En la tercera sucesión ya se nos proporciona el término general.
La primera y la tercera sucesión son crecientes porque su diferencia es positiva (\(d=6\) en una y \(d=3\) en la otra). La segunda sucesión es decreciente porque su diferencia es negativa (\(d=-3\)).
Problema 9 
Calcular el término general de las siguientes sucesiones:
-
6, 13, 20, 27,...
-
6, 2, -2, -6,...
-
0, -1/2, -1, -3/2,...
Resolvemos:
Para calcular el término general se necesitan el primer término y la diferencia.
-
6, 13, 20, 27,...
Calculamos la diferencia restando términos consecutivos:
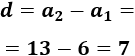
Como la diferencia es 7 y el primer término es 6, el término general es
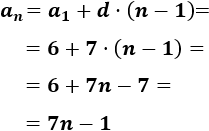
-
6, 2, -2, -6,...
Calculamos la diferencia restando términos consecutivos:
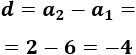
Como la diferencia es -4 y el primer término es 6, el término general es
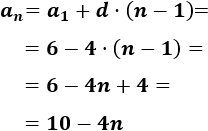
-
0, -1/2, -1, -3/2,...
Calculamos la diferencia restando términos consecutivos:
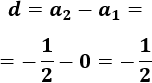
Como la diferencia es -1/2 y el primer término es 0, el término general es
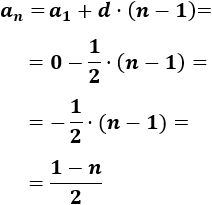
Problema 10 
Calcular el término \(a_1\) de las sucesiones aritméticas a partir de los datos dados:
-
\( a_4=11,\ a_5=14 \)
-
\( a_4=23,\ d=4 \)
-
\( a_4=28,\ a_6=34 \)
Resolvemos:
-
\( a_4=11,\ a_5=14 \)
Calculamos la diferencia de la sucesión:
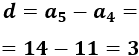
Aplicamos el término general para calcular el cuarto término
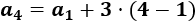
Como conocemos \(a_4=11\), podemos calcular \(a_1\) resolviendo una ecuación sencilla:
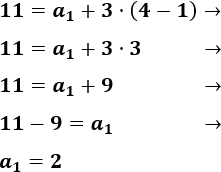
-
\( a_4=23,\ d=4 \)
Aplicamos la fórmula del término general con \(n=4\):
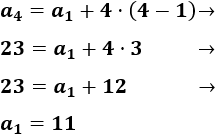
-
\( a_4=28,\ a_6=34 \)
El quinto término se obtiene sumando la diferencia \(d\) al cuarto término:
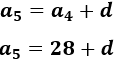
El sexto término se obtiene sumando la diferencia \(d\) al quinto término:
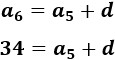
Podemos sustituir la expresión de \(a_5\) en la ecuación anterior:
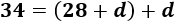
Resolvemos la ecuación:
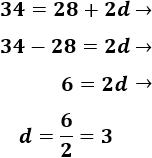
La diferencia es \(d=3\).
Ahora aplicamos el término general con \(n=4\) para calcular el primer término:
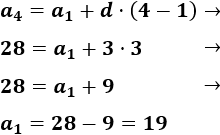
Problema 11 
Calcular la suma de los 10 primeros términos de las siguientes sucesiones:
-
3, 10, 17,...
-
12, 15, 18,...
-
15, 12, 9,...
Resolvemos:
Emplearemos la primera fórmula para la suma:
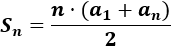
Necesitaremos calcular \(a_{10}\) para poder aplicar la fórmula.
-
3, 10, 17,...
La diferencia de esta sucesión es \(d=7\) . Por tanto, el término \(a_{10}\) es
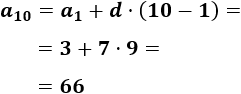
Calculamos la suma de los 10 primeros términos:
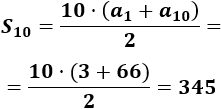
-
12, 15, 18,...
La diferencia de esta sucesión es \(d=3\) . Por tanto, el término \(a_{10}\) es
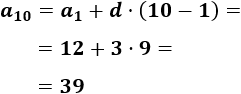
Calculamos la suma de los 10 primeros términos:
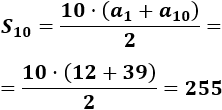
-
15, 12, 9,...
La diferencia de esta sucesión es \(d=-3\) . Por tanto, el término \(a_{10}\) es
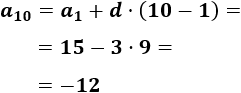
Calculamos la suma de los 10 primeros términos:
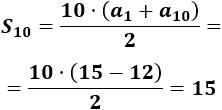
Problema 12 
Calcular la suma de los 10 primeros términos las sucesiones a partir de los datos dados:
-
\( a_1=5,\ a_{10}=14 \)
-
\( a_1=5,\ d=4 \)
-
\( a_2=18,\ d=5 \)
Resolvemos:
La fórmula para calcular la suma es
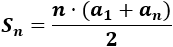
-
\( a_1=5,\ a_{10}=14 \)
Sustituimos los datos en la fórmula:
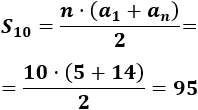
-
\( a_1=5,\ d=4 \)
Tenemos que calcular \(a_{10}\) para aplicar la fórmula:
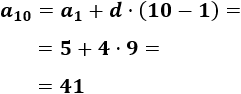
Calculamos la suma:
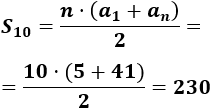
-
\( a_2=18,\ d=5 \)
Tenemos que calcular \(a_1\) y \(a_{10}\) para aplicar la fórmula.
Como \(a_2\) se obtiene sumando la diferencia \(d\) al término \(a_1\), podemos calcular \(a_1\) restando \(d\) al término \(a_2\):
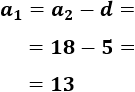
Calculamos el término \(a_{10}\):
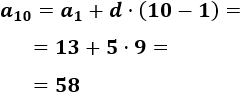
Calculamos la suma:
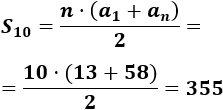
Problema 13 
Encontrar una progresión aritmética cuyo primer término sea 3 y que sus tres primeros términos sumen 12.
Resolvemos:
La fórmula para calcular la suma es
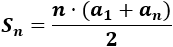
Como los 3 primeros términos deben sumar 12,
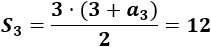
Resolvemos la ecuación obtenida:
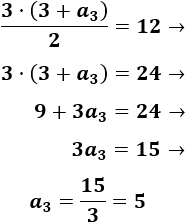
Sabemos que el primer término es 3 y que el tercero es 5. Podemos calcular el segundo. Los tres primeros términos son
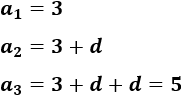
Calculamos la diferencia resolviendo la ecuación anterior:
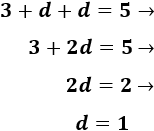
Por tanto, la diferencia es \(d = 1\) y el segundo término es
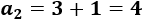
La sucesión es 3, 4, 5, 6, 7,...
Problema 14 
Calcular cuántos números impares hay entre 20 y 50 y calcular su suma.
Resolvemos:
La diferencia de la sucesión de los impares es \(d=2\).
El primer número impar comprendido entre 20 y 50 es 21 y el último es 49:
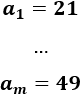
Observad que \(m\) es el número de números impares entre 20 y 50. Para calcularlo, utilizaremos la diferencia y la fórmula del término general:
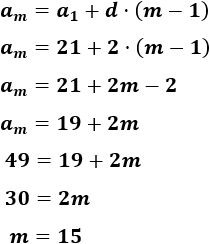
Por tanto, hay 15 números impares entre 20 y 50. Calculamos su suma:
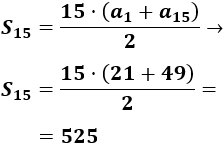
Problema 15 
El primer término de una sucesión aritmética es \(a_1=12\) y la suma de los 5 primeros términos es \(S_5=90\) . Calcular el término \(a_5\) y el término general \(a_n\).
Resolvemos:
La fórmula para calcular la suma es
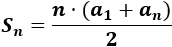
Como conocemos \(S_5=90\) y \(a_1=12\), tenemos
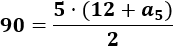
Despejamos el término \(a_5\) de la ecuación anterior:
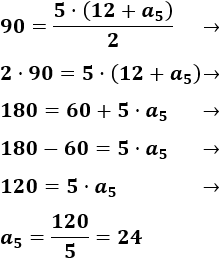
Por tanto, el quinto término es
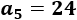
A partir del primer y quinto término podemos calcular la diferencia:
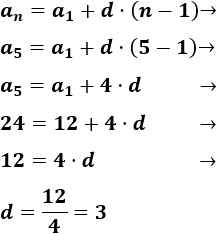
Como conocemos el primer término y la diferencia, conocemos el término general: