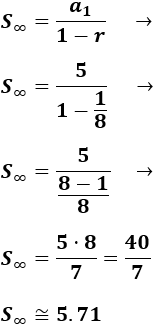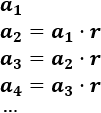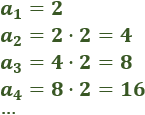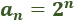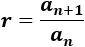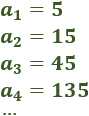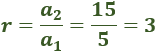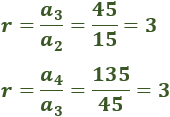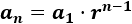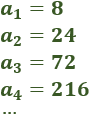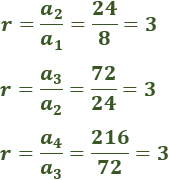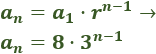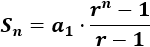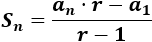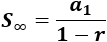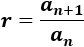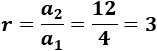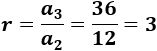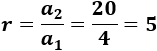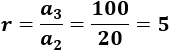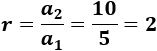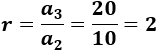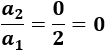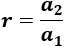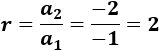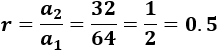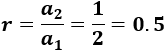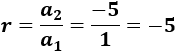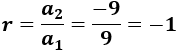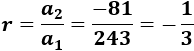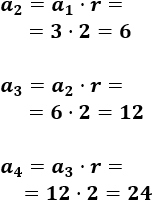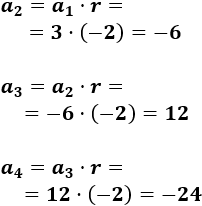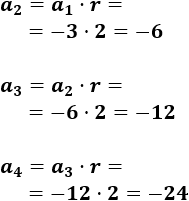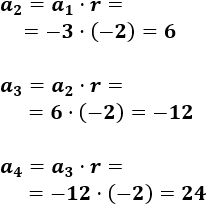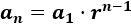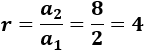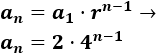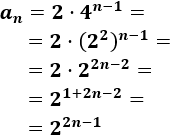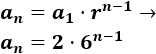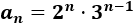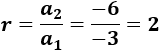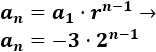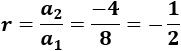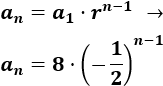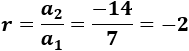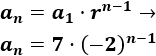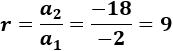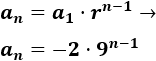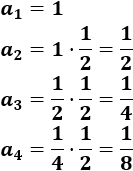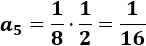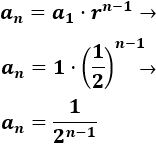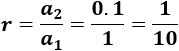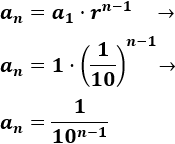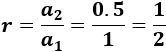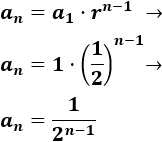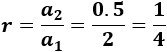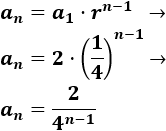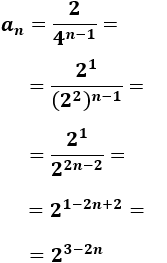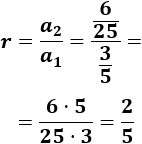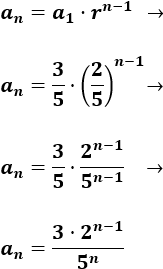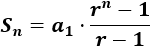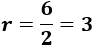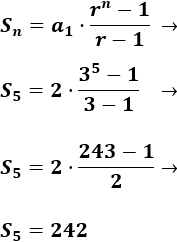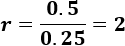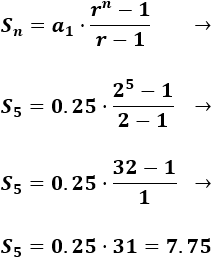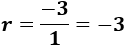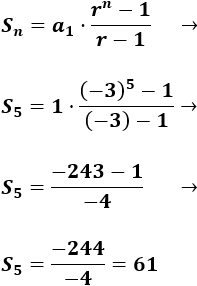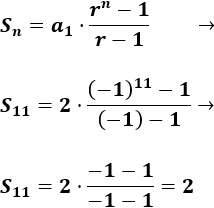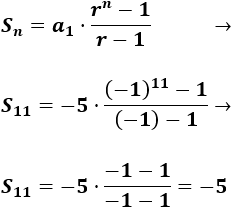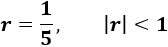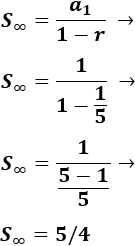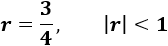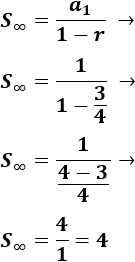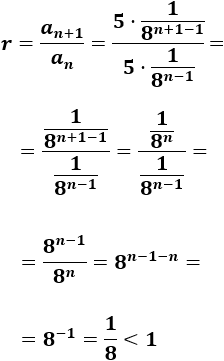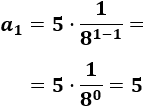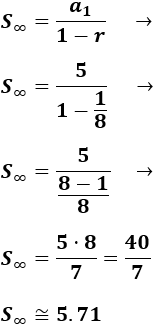Problema 1 
Determinar la razón de las siguientes progresiones geométricas:
-
4, 12, 36, 108,...
-
4, 20, 100, 500,...
-
5, 10, 20, 40,...
Ver solución
Calculamos la razón dividiendo términos consecutivos:
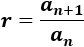
-
4, 12, 36, 108,...
Dividimos el segundo término entre el primero:
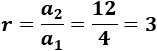
Dividimos el tercero entre el segundo para comprobar que la razón no cambia:
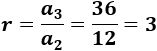
La razón es \(d = 3\).
-
4, 20, 100, 500,...
Dividimos el segundo término entre el primero:
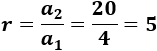
Dividimos el tercero entre el segundo:
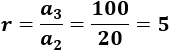
La razón es \(d = 5\).
-
5, 10, 20, 40,...
Dividimos el segundo término entre el primero:
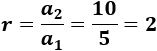
Dividimos el tercero entre el segundo:
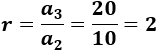
La razón es \(d = 2\).
Nota: si tenemos la certeza de que la progresión es geométrica, es suficiente con calcular la razón entre dos términos consecutivos; en caso contrario, cuantos más calculamos, mejor.
Problema 2 
¿Cuál de las siguientes sucesiones no es geométrica?
-
1, 3, 9, 27,...
-
1, -1, 1, -1,...
-
2, 0, 2, 0, 2,...
Ver solución
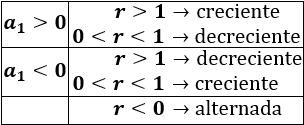
La primera y la segunda progresión son geométricas con razón \(r=3\) y \(r=-1\), respectivamente. La primera es creciente y la segunda es alternada.
La tercera sucesión no es geométrica. Si dividimos el segundo término entre el primero obtenemos
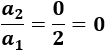
Pero podemos dividir el tercer término entre el segundo porque el segundo término es 0.
Si la sucesión fuese geométrica, todos los siguientes términos deberían ser 0.
Nota: la tercera sucesión tampoco es aritmética.
Problema 3 
Calcular la razón de las siguientes progresiones decrecientes:
-
-1, -2, -4, -8,...
-
64, 32, 16, 8,...
-
2, 1, 0.5, 0.25,...
Ver solución
Para calcular la razón vamos a dividir el segundo término entre el primero:
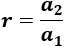
-
-1, -2, -4, -8,...
La razón es \(r=2\) ya que
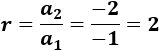
-
64, 32, 16, 8,...
La razón es \(r=0.5\) ya que
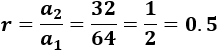
-
2, 1, 0.5, 0.25,...
La razón es \(r=0.5\) ya que
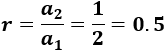
Problema 4 
Calcular la razón de las siguientes progresiones alternadas:
-
1, -5, 25, -125,...
-
9, -9, 9, -9,...
-
243, -81, 27, -9,...
Ver solución
Como las sucesiones son alternadas, sus respectivas razones son negativas.
-
1, -5, 25, -125,...
La razón es \(r=-5\) ya que
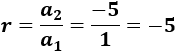
-
9, -9, 9, -9,...
La razón es \(r=-1\) ya que
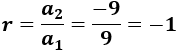
-
243, -81, 27, -9,...
La razón es \(r=-1/3\) ya que
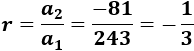
Problema 5 
Calcular los tres siguientes términos de las sucesiones a partir de los datos dados:
-
\(a_1=3\), \(r=2\)
-
\(a_1=3\), \(r=-2\)
-
\(a_1=-3\), \(r=2\)
-
\(a_1=-3\), \(r=-2\)
Determinar si son crecientes, decrecientes o alternadas.
Ver solución
Vamos a calcular cada término multiplicando el término anterior por la razón.
-
\(a_1=3\), \(r=2\)
Los siguientes términos son
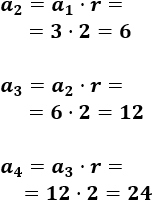
-
\(a_1=3\), \(r=-2\)
Los siguientes términos son
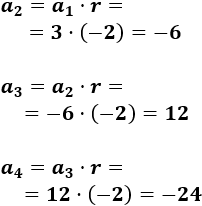
-
\(a_1=-3\), \(r=2\)
Los siguientes términos son
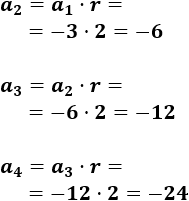
-
\(a_1=-3\), \(r=-2\)
Los siguientes términos son
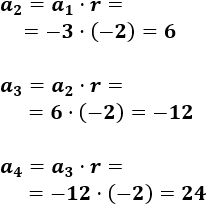
La segunda y la cuarta progresión son alternadas. La primera es creciente y la tercera es decreciente.
Nota: los términos de las sucesiones son iguales en módulo (es decir, si les quitamos el signo).
Problema 6 
Calcular el término general de las siguientes progresiones geométricas:
-
2, 8, 32, 128,...
-
\(a_1=2\), \(r=6\)
-
\(a_1=-3\), \(a_2=-6\)
Solución
El término general de una sucesión geométrica es
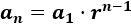
Necesitamos el primer término y la razón para calcularlo.
-
2, 8, 32, 128,...
Calculamos la razón dividiendo el segundo término entre el primero:
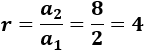
Por tanto, el término general es
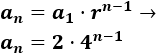
Podemos simplificar la fórmula aplicando las propiedades de las potencias:
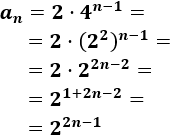
-
\(a_1=2\), \(r=6\)
El término general es
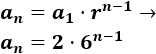
También podemos escribir la fórmula como
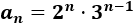
-
\(a_1=-3\), \(a_2=-6\)
Calculamos la razón dividiendo los términos:
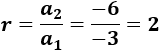
El término general es
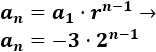
Problema 7 
Calcular el término general de las siguientes progresiones geométricas:
-
8, -4, 2, -1,...
-
7, -14, 28, -56,...
-
-2, -18, -162, -1458,...
Ver solución
-
8, -4, 2, -1,...
La razón es
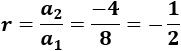
El término general es
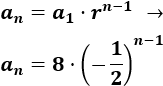
-
7, -14, 28, -56,...
La razón es
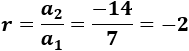
El término general es
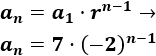
-
-2, -18, -162, -1458,...
La razón es
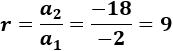
El término general es
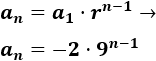
Problema 8 
Dada la progresión
\begin{matrix}
a_1 & = & 1 \\
a_2 & = & \frac{1}{2} \\
a_3 & = & \frac{1}{4} \\
a_4 & = & \frac{1}{8} \\
...
\end{matrix}
Contestar:
-
¿Es una progresión geométrica? Calcular la razón en caso afirmativo.
-
¿Es creciente, decreciente o alternada?
-
¿Cuál es el término \(a_5\)?
-
¿Cuál es el término general \(a_n\)?
Ver solución
-
Es una progresión geométrica porque cada término se obtiene multiplicando al anterior por la razón \(r=1/2\):
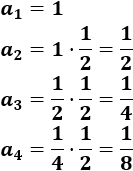
-
Es decreciente porque el primer término es positivo y la razón es \(0 < r < 1\). Observad que el denominador va aumentado y el numerador es siempre 1.
-
Calculamos el quinto término multiplicando el cuarto por la razón:
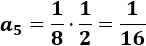
-
El término general es
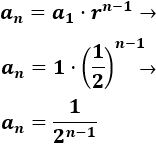
Problema 9 
Calcular el término general de las siguientes progresiones geométricas:
-
1, 0.1, 0.01, 0.001,...
-
1, 0.5, 0.25, 0.125,...
-
2, 0.5, 0.125, 0.03125,...
Solución
-
1, 0.1, 0.01, 0.001,...
Calculamos la razón:
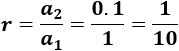
Por tanto, el término general es
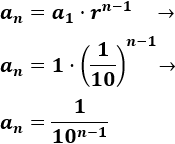
-
1, 0.5, 0.25, 0.125,...
La razón es
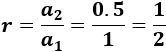
Y el término general es
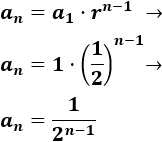
-
2, 0.5, 0.125, 0.03125,...
Calculamos la razón:
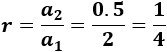
El término general es
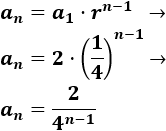
Podemos simplificar más:
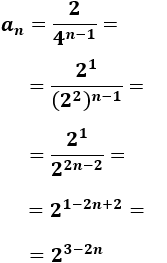
Problema 10 
Calcular el término general de la progresión geométrica
$$\frac{3}{5},\ \frac{6}{25},\ \frac{12}{125},\ ... $$
Ver solución
Dividimos el segundo término entre el primero para calcular la razón:
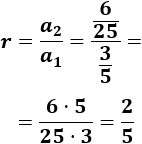
El término general es
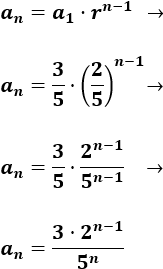
Problema 11 
Calcular la suma de los 5 primeros términos de las siguientes sucesiones geométricas (utilizando la fórmula para la suma):
-
2, 6, 18,...
-
0.25, 0.5, 1,...
-
1, -3, 9,...
Ver solución
Utilizaremos la fórmula
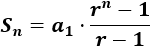
-
2, 6, 18,...
Calculamos la razón:
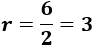
Calculamos la suma:
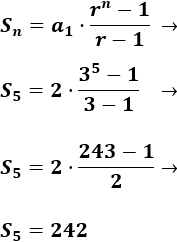
-
0.25, 0.5, 1,...
Calculamos la razón:
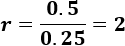
Y la suma:
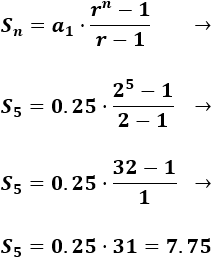
-
1, -3, 9,...
La razón es
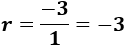
La suma es
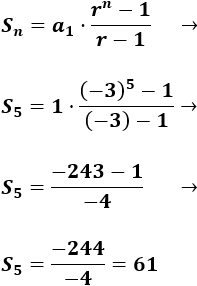
Problema 12 
Calcular la suma de los 11 primeros términos de las siguientes progresiones alternadas:
-
2, -2, 2, -2,...
-
-5, 5, -5, 5,...
Ver solución
La razón de las dos sucesiones es \(r=-1\).
-
2, -2, 2, -2,...
Calculamos la suma:
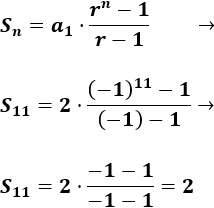
-
-5, 5, -5, 5,...
Calculamos la suma:
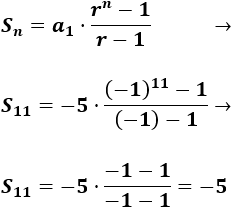
Problema 13 
Sumar todos los términos de la sucesión
$$1,\ \frac{1}{5},\ \frac{1}{25},\ ... $$
Ver solución
Se pueden sumar todos los términos porque la razón es menor que 1 en módulo:
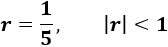
Calculamos la suma:
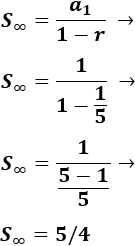
Problema 14 
Sumar todos los términos de la progresión
$$1, \frac{3}{4},\ \frac{9}{16},\ \frac{27}{64},\ ... $$
Ver solución
Se pueden sumar todos los términos porque la razón es
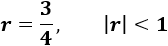
Calculamos la suma:
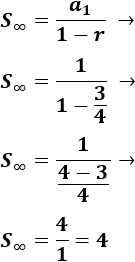
Problema 15 
Sumar todos los términos de la sucesión
$$ a_n =5\cdot \frac{1}{8^{n-1}}, \ n≥ 1 $$
Ver solución
Calculamos la razón:
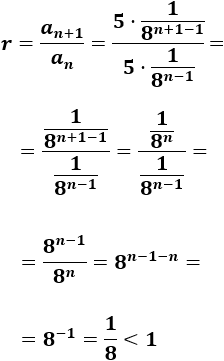
Calculamos el primer término:
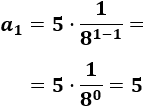
Como la razón cumple \(|r|<1\), podemos sumar todos los términos: