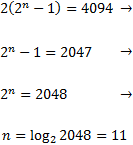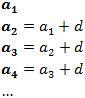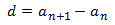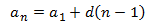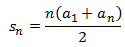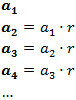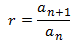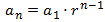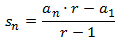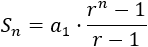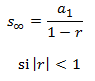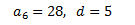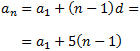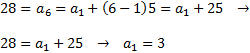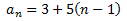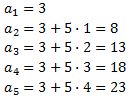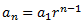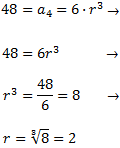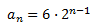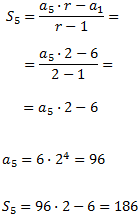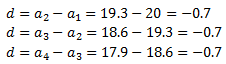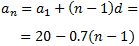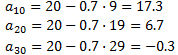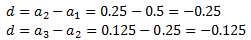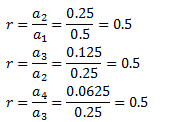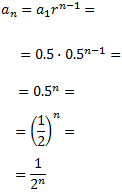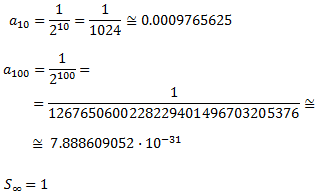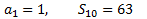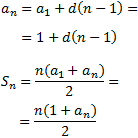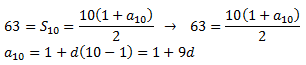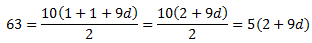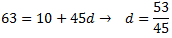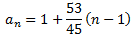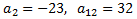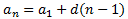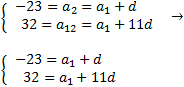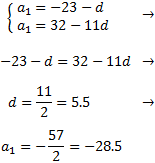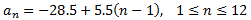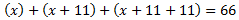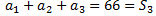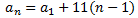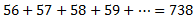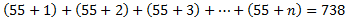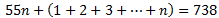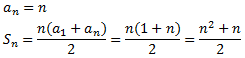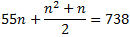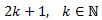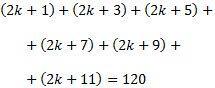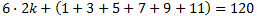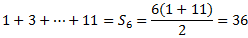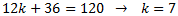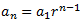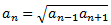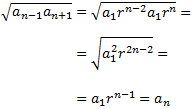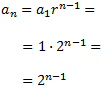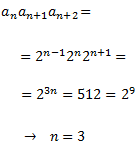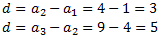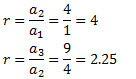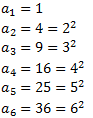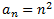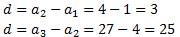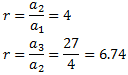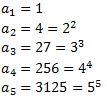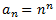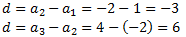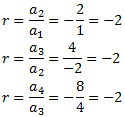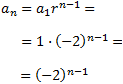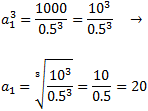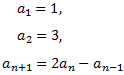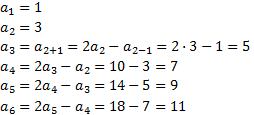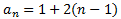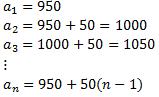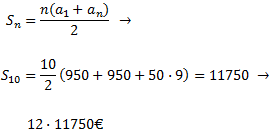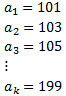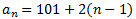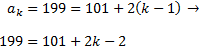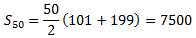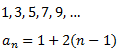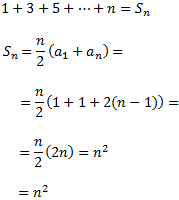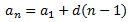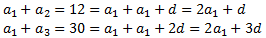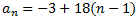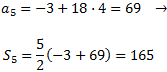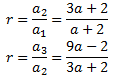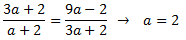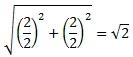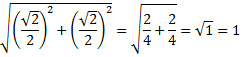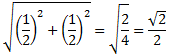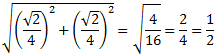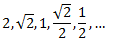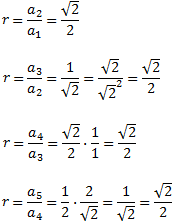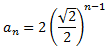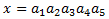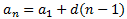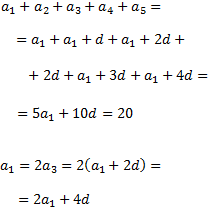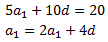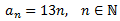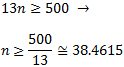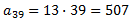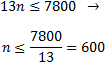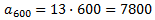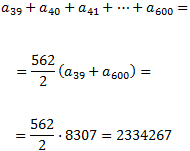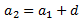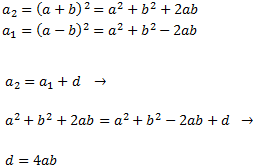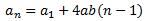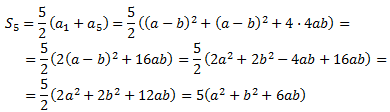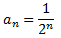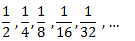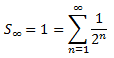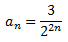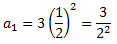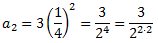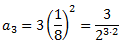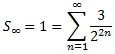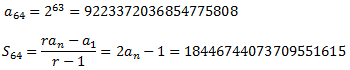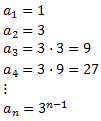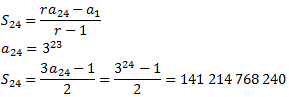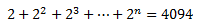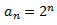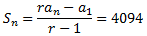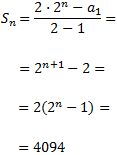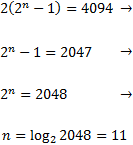Problema 1 
En una progresión aritmética, sabemos que el sexto término es 28 y que la diferencia es 5. Calcular el término general y los 5 primeros términos.
SOLUCIÓN
Conocemos el término 6-ésimo y la diferencia:
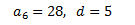
Queremos calcular el término general de la sucesión, \(a_n\), que sabemos
que es de la forma
$$ a_n = a_1 + (n-1)\cdot d$$
Como la diferencia es \(d = 5\), tenemos
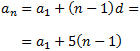
Necesitamos calcular el primer término de la sucesión, \(a_1\). Para ello,
aplicamos la fórmula para el caso \( n = 6\) ya que sabemos que
\( a_6 = 28\). Sustituimos en la fórmula:
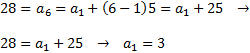
Por tanto, el término general de la sucesión aritmética es
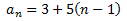
Los cinco primeros términos son
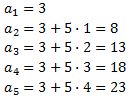
Nota: hemos calculado los términos aplicando la fórmula obtenida, pero una
vez sabemos que el primer término es 3 y que la diferencia es 5, podemos obtener
fácilmente los términos sumando la diferencia.
Problema 2 
En una progresión geométrica, sabemos que el primer término es 6 y el cuarto es 48. Calcular el término general y la suma de los 5 primeros términos.
SOLUCIÓN
Conocemos el primer y el cuarto término:

Como la progresión es geométrica, su fórmula general es de la forma
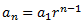
De dicha fórmula conocemos el término \(a_1\), pero no conocemos la razón,
\(r\). Para calcularla, aplicamos la fórmula para el caso \(n=4\) porque sabemos
que \( a_4 = 48\):
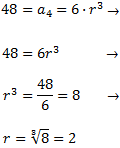
Por tanto, la razón es \(r = 2\) y el término general es
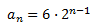
Para calcular la suma de los 5 primeros términos, aplicamos la fórmula. Necesitaremos calcular el término \(a_5\):
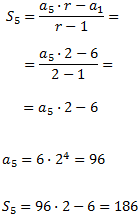
Problema 3 
Encontrar el término general de la sucesión
20, 19.3, 18.6, 17.9, …
¿Es aritmética o geométrica? Encontrar los términos: décimo (10), vigésimo (20)
y trigésimo (30).
SOLUCIÓN
Si la sucesión es aritmética, entonces la diferencia entre dos
términos consecutivos siempre es la misma.
Buscamos la diferencia:
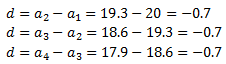
Se trata de una sucesión aritmética con diferencia d = -0.7 (es una sucesión decreciente, d < 0). Por tanto, el término general es
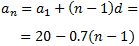
Aplicando dicha fórmula podemos calcular los terminos décimo, vigésimo y trigésimo:
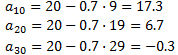
Problema 4 
Encontrar el término general de la sucesión
0.5, 0.25, 0.125, 0.0625,...
¿Es aritmética o geométrica? Calcular los términos n- ésimos para los valores de n = 10, 100.
Se sabe que la suma de los infinitos términos de esta sucesión es 1 (ejercicio 26). Razonar cómo es posible
que la suma de infinitos términos positivos no sea infinita.
SOLUCIÓN
Buscamos la diferencia:
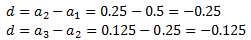
Como los valores no coinciden, la sucesión no es aritmética.
Buscamos la razón:
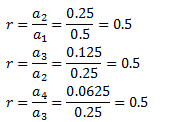
Se trata de una sucesión geométrica de razón r = 0.5 (decreciente puesto que r < 1).
Como conocemos el primer término y la razón, el término general es
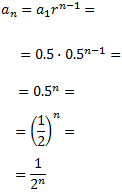
Así, podemos calcular los términos 10-ésimo y 100-ésimo:
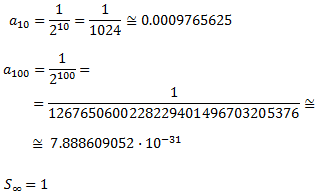
Observamos que los términos de la sucesión son muy pequeños: el décimo tiene tres ceros
detrás de la coma y el centésimo, tiene treinta.
Aunque los términos de la sucesión son positivos, éstos son cada vez más pequeños y muy próximos
a 0. De este modo, al sumarlos, a penas incrementa el valor,
aunque sumemos infinitos números.
Problema 5 
En una progresión aritmética, sabemos que el primer término es 1 y
la suma de los 10 primeros términos es 63. Calcular el término general.
SOLUCIÓN
Conocemos el primer término y la suma de los diez primeros términos:
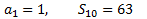
Utilizaremos las fórmulas del término general y de la suma (de una progresión aritmética) para poder calcular la diferencia, \(d\). Dichas fórmulas son:
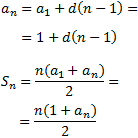
Hemos escrito en las fórmulas \(a_1 = 1\).
Sustituimos los datos conocidos:
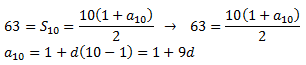
Podemos sustituir \( a_{10}\) en la primera fórmula:
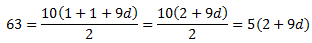
De la ecuación resultante obtenemos d:
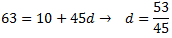
Luego la diferencia es \(d = 53/45\) y el término general es
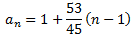
Problema 6 
En una progresión aritmética finita, el
segundo término es -23 y el último 32. Si
se sabe que hay 12 términos, calcular el término general.
SOLUCIÓN
Conocemos el segundo término y el duodécimo:
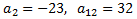
Por ser aritmética, sabemos que la fórmula general de la misma es de la forma
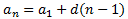
Con los datos que conocemos, podemos construir un sistema de ecuaciones para calcular
el primer término y la diferencia:
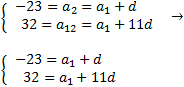
Resolvemos el sistema por el método de igualación:
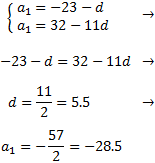
Por tanto, el término general es
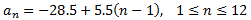
Nota: hemos indicado los valores que puede tomar n ya que la sucesión es finita.
Problema 7 
La suma de tres términos consecutivos de una sucesión aritmética cuya diferencia
es 11 vale 66. Encontrar dichos términos.
SOLUCIÓN
Como la diferencia de la sucesión es 11, la diferencia entre términos consecutivos es 11. Entonces, si uno de los términos es \(x\), su consecutivo es \(x+11\) y el consecutivo de éste es \(x+11+11\).
Sabemos que los 3 términos consecutivos han de sumar 66, así que tenemos
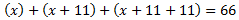
Es decir, tenemos una ecuación de primer grado cuya solución es 11:

Luego los números son 11, 22, 33.
La ecuación la podemos expresar en términos de una progresión como
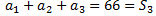
es decir, como la suma de los tres primeros términos de una progresión cuyo término general es
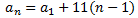
Problema 8 
La suma de n números naturales
consecutivos a partir de 55 (sin incluirlo) vale 738. Encontrar n.
SOLUCIÓN
El enunciado nos dice que
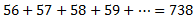
Así, \(n\) es el número de sumandos a la izquierda de la igualdad.
Podemos expresar la ecuación anterior como
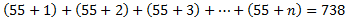
Es decir,
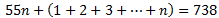
En realidad, el interior del paréntesis es la
suma de los n primeros términos de una
progresión aritmética con diferencia 1 y cuyo
primer término es 1, esto es
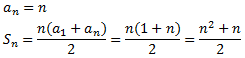
Por tanto, podemos reescribir la ecuación como
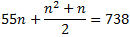
Tenemos entonces una ecuación segundo grado cuyas
soluciones son
n = -123, 12. Como n
representa la cantidad de sumandos, ha de ser un
número natural (entero positivo), de modo que n = 12.
Problema 9 
La suma de 6 números impares consecutivos vale 120. Encontrar dichos números.
SOLUCIÓN
Un número impar es de la forma
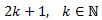
Si el más pequeño de los 6 números impares es \(2k+1\), sus consecutivos se obtienen sumando \(2\). Por tanto, buscamos la \(k\) que cumple
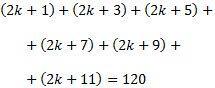
Simplificando,
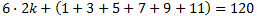
El interior del paréntesis es la suma de los 6 primeros términos de una sucesión aritmética de diferencia 2 y que empieza en 1, es decir,
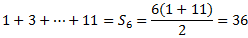
Por tanto,
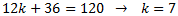
Los números son 15, 17, 19, 21, 23, 25.
Problema 10 
Demostrar que en cualquier sucesión geométrica
positiva, cada término es la raíz cuadrada del producto de su
término anterior por su término siguiente. Es decir,
$$ a_n = \sqrt{a_{n-1}\cdot a_{n+1}}$$
SOLUCIÓN
El término general de una sucesión geométrica es
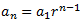
y queremos demostrar que
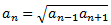
Para demostrarlo, calculamos \(a_{n-1}\) y \(a_{n+1}\) usando el término general:
$$a_{n-1} = a_1 r^{n-1-1} = a_1 r^{n-2} $$
$$a_{n+1} = a_1 r^{n+1-1} = a_1 r^{n} $$
y sustituimos en el radicando. Quedará demostrado al obtener que dicha raíz es justamente el término \(a_n\):
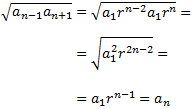
Observaciones:
- Hemos aplicando las propiedades de las potencias para simplificar.
-
La exigencia de que la sucesión sea positiva es porque, de este modo, la raíz cuadrada de \(a_1^2\) es \(a_1\) y no su valor absoluto.
- Como la sucesión es positiva, su razón también lo es. Por ello, tampoco
escribimos el valor absoluto al simplificar la raíz de \( r^{2(n-1)}\).
Problema 11 
Una progresión geométrica comienza en 1 y tiene razón 2.
Encontrar los tres términos consecutivos (de la sucesión) cuyo producto es 512.
SOLUCIÓN
El término general de la progresión es
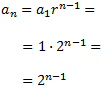
No sabemos la posición que ocupan los tres términos, pero sí sabemos
que son consecutivos. Por tanto, si el primero de ellos es \(a_n\), los
otros dos son \(a_{n+1}\) y \(a_{n+2}\). Entonces, utilizando el término general, el producto de dichos términos es
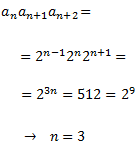
Por tanto, los términos son el tercero, el cuarto y el quinto: 4, 8, 16.
Problema 12 
Encontrar el término general de la sucesión
1, 4, 9, 16, 25, 36, 49, ...
¿Es aritmética o geométrica?
SOLUCIÓN
Comprobamos si es aritmética restando términos consecutivos:
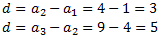
No lo es puesto que las diferencias no coinciden.
Comprobamos si es geométrica dividiendo términos consecutivos:
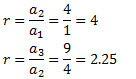
No lo es puesto que la razón no es la misma.
Luego la progresión no es ni aritmética ni geométrica. Tendremos que deducir por nuestra cuenta cuál es el término general.
Lo primero que hacemos es fijarnos en la relación entre la posición de cada término y su valor:
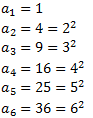
Por tanto, deducimos que el término general es
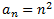
No es una progresión aritmética ni geométrica.
En esta sucesión no podemos utilizar
la fórmula que conocemos para sumar \(n\) términos.
Problema 13 
Encontrar el término general de la sucesión
1, 4, 27, 256, 3125, ...
¿Es aritmética o geométrica?
SOLUCIÓN
Comprobamos si es aritmética:
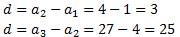
No lo es. Comprobamos si es geométrica:
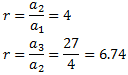
No lo es. Nos fijamos en la relación entre la posición de cada término y su valor:
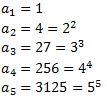
Por tanto, deducimos que el término general es
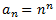
No es una progresión aritmética ni geométrica.
Problema 14 
Encontrar el término general de la sucesión
1, -2, 4, -8, 16,...
¿Es aritmética o geométrica?
SOLUCIÓN
Comprobamos si es aritmética:
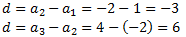
No lo es. Comprobamos si es geométrica:
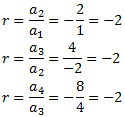
Por tanto, es geométrica con razón r = -2 y, por tanto, su término general es
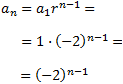
Como la razón es negativa, la sucesión es alternada.
Esto implica que cada término tiene un signo distinto. En esta sucesión en particular, los términos de posición par son negativos y los otros son positivos.
Problema 15 
Calcular la suma de los tres primeros términos
de una sucesión geométrica de razón 0.5
sabiendo que su producto es 1000.
SOLUCIÓN
Como la sucesión es geométrica y conocemos la razón, el término
general es
$$ a_n = a_1\cdot 0.5^{n-1} $$
Sabemos que el producto de los tres primeros términos es 1000. Dicho
matemáticamente,
$$ a_1 \cdot a_2 \cdot a_3 = 1000 $$
Sustituimos \(a_1\), \(a_2\) y \(a_3\) de la expresión
anterior por el término general con \(n=1\), \(n=2\) y
\(n=3\), respectivamente:
$$ 1000 = a_1\cdot (a_1 \cdot 0.5)\cdot (a_1\cdot 0.5^2) $$
Con lo que obtenemos la ecuación
$$ 1000 = a_1 ^3 \cdot 0.5^3$$
Esta ecuación nos proporciona el primer término:
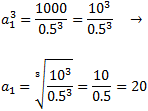
Por tanto, la sucesión es 20, 10, 5,... y la suma de los tres primeros términos es 35.
Problema 16 
Considérese la sucesión dada por recurrencia
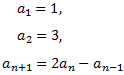
Calcular los términos que sean necesarios para
poder deducir su término general.
SOLUCIÓN
Aplicaremos la fórmula dada para calcular, uno a uno,
los primeros términos de la sucesión:
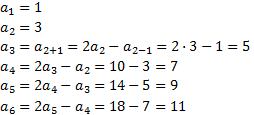
Luego la sucesión es 1, 3, 5, 7, 9, 11,... que es la sucesión de los números impares.
Por tanto, su término general es
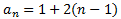
Se trata de una sucesión aritmética de diferencia d = 2.
Nota: al expresar la sucesión por
recurrencia, para calcular el término \(n+1\)-ésimo se
necesita calcular previamente todos términos que le
preceden: para calcular \(a_{n+1}\) hacen falta
\(a_{n}\) y \(a_{n-1}\), pero para calcular
\(a_{n}\) hacen halta \(a_{n-1}\) y \(a_{n-2}\) y, asi,
sucesivamente hasta \(a_1\). No ocurre lo mismo con el término general. Ahora bien, para algunas sucesiones no se puede encontrar una fórmula del término general.
Problema 17 
El sueldo de un trabajador es de 950€ mensuales
y cada año se incrementa en 50€ (cada mes).
Calcular cuánto dinero ganará en los 10 años siguientes.
SOLUCIÓN
Construimos una sucesión cuyo término n-ésimo es el sueldo mensual en el año n-ésimo:
En el primer año, el sueldo mensual es de 950. En el segundo año, el sueldo mensual es de 1000. En el tercero, 1050. Luego la sucesión es
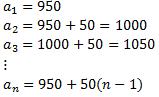
Se trata de una progresión aritmética con diferencia d = 50.
En total, en el año n-ésimo el sueldo es 12·an porque hay
12 meses en un año y cada término representa el sueldo
mensual. Por tanto, debemos multiplicar por 12 la suma
de los 10 primeros términos:
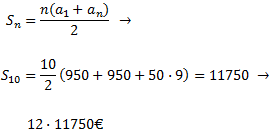
En 10 años, la cifra asciende a 12·11750 = 141000€.
Problema 18 
Calcular la suma de todos los números impares comprendidos entre 100 y 200.
SOLUCIÓN
Construimos la progresión formada por dichos números:
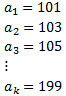
Hemos usado k porque no sabemos qué posición ocupa el último término. Es una progresión aritmética con diferencia d = 2 y con término general
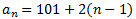
Buscamos la posición del último término:
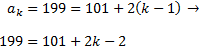
Resolvemos la ecuación y obtenemos k = 50.
Por tanto, la suma será
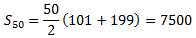
Problema 19 
Demostrar que la suma de los n primeros impares es n2.
SOLUCIÓN
Consideremos la sucesión de los números impares
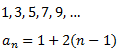
Es una sucesión aritmética con diferencia d = 2. Queremos calcular la suma de los n primeros términos, es decir,
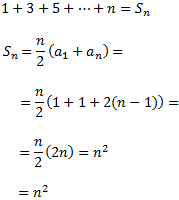
Problema 20 
En una progresión aritmética, la suma de los dos primeros términos
es 12 y la suma del primero con el tercero es 30. Hallar el término
general y calcular la suma de los cinco primeros términos.
SOLUCIÓN
Como la progresión es aritmética, el término general es
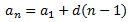
Tenemos los datos:
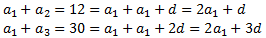
Resolvemos el sistema de ecuaciones obteniendo el primer término y la diferencia:

Luego el término general es
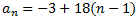
Y la suma de los cinco primeros es
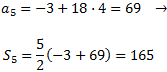
Problema 21 
Calcular el valor del parámetro a para que los números a+2, 3a+2, 9a-2
sean los tres primeros términos de una progresión geométrica.
Ver solución
Para que formen una progresión geométrica de razón r se tiene que cumplir
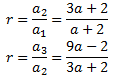
Como la razón debe ser constante, igualamos ambas expresiones y así obtenemos a:
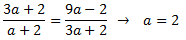
La sucesión es 4, 8, 16,… y tiene razón r = 2.
Problema 22 
En un cuadrado de lado 2 se unen los puntos medios de sus lados
para obtener otro cuadrado inscrito. Se repite el proceso sucesivamente
con los cuadrados obtenidos:
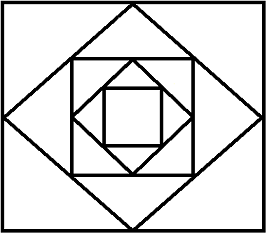
Calcular la sucesión cuyo término n-ésimo
corresponde con la longitud del lado del cuadrado n-ésimo.
¿Qué tipo de sucesión es?
Ver solución
Utilizaremos el teorema de Pitágoras ( h 2 = a 2 + b 2 ) para calcular los lados.
El lado del cuadrado inicial mide 2.
El lado del primer cuadrado mide
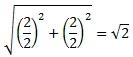
El lado del segundo cuadrado mide
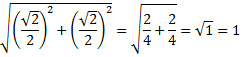
El lado del tercer cuadrado mide
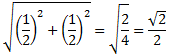
El lado del cuarto cuadrado mide
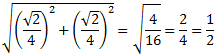
Tenemos la sucesión
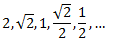
Es una sucesión geométrica puesto que la razón entre términos consecutivos se mantiene constante:
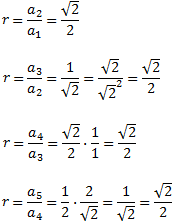
Por tanto, el término general es
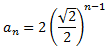
Problema 23 
Calcular un número sabiendo que sus cinco cifras están
colocadas en progresión aritmética, que la suma de todas ellas
es 20 y que la primera es el doble de la tercera.
Ver solución
Representamos el numero como
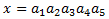
El término general de la sucesión que proporciona las cifras es el de una sucesión aritmética:
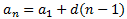
De la suma de todas las cifras y de la relación existente entre la primera y la tercera obtenemos las siguientes ecuaciones:
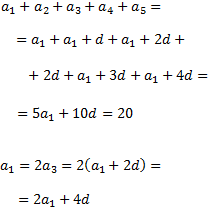
Tenemos el sistema de ecuaciones
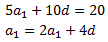
cuya solución es

La sucesión es 8,6,4,2,0,… Y, por tanto, el número buscado es x = 86420.
Problema 24 
Calcular la suma de los múltiplos de 13 comprendidos entre los números 500 y 7800 inclusive.
Ver solución
Consideremos la sucesión aritmética formada por los múltiplos de 13:
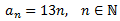
Obsérvese que se trata de una sucesión aritmética con diferencia 13.
Buscamos el primer término que sea mayor o igual que 500:
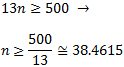
Por tanto, el primer múltiplo de 13 y mayor o igual que 500 es
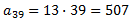
Ahora buscamos el último múltiplo de 13, que debe cumplir
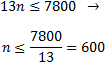
Es decir, es el término
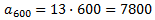
Calculamos la suma de todos los términos:
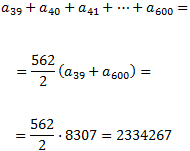
donde hemos usado la fórmula de la suma de las progresiones aritméticas, siendo 562 el número de términos que hemos sumado.
Problema 25 
Los dos primeros términos de una progresión aritmética
son a1 = (a - b)2 y a2 = (a + b)2.
Calcular la diferencia de la progresión y la suma de los 5 primeros términos.
Ver solución
Como forman parte de una progresión aritmética, si la diferencia es d, sabemos
que el segundo término es
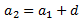
Desarrollamos los cuadrados y calculamos la diferencia d:
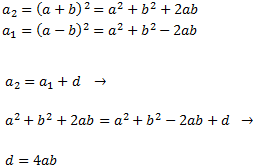
El término general es
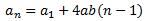
La suma de los 5 primeros términos es
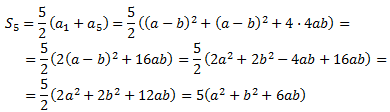
Problema 26 
Demostrar que la suma infinita de la sucesión
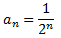
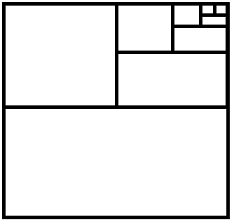
es 1 con la ayuda del siguiente diagrama que representa un cuadrado de lado 1.
Ver solución
Calculamos los primeros términos de la sucesión:
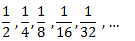
Como el lado del cuadrado es 1, su área es 1. Así pues, el área de la mitad del cuadrado es 1/2. El área de la mitad de esta mitad es 1/4. Y así, sucesivamente:
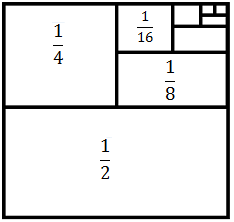
Es decir, las áreas de los cuadrados o rectángulos que se obtienen al dividir por la mitad son los términos de la sucesión. Para infinito, habremos recubierto el cuadrado completo, que tiene área 1. Por tanto, la suma de todos los términos de la sucesión es 1. Así que
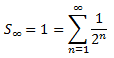
Problema 27 
Demostrar que la suma infinita de la progresión geométrica
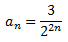
es 1 con la ayuda del siguiente diagrama de cuadrados de lado 1
en los que el área amarilla del n-ésimo cuadrado vale lo mismo
que el término n-ésimo de la progresión.
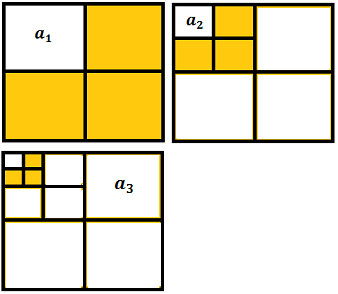
Ver solución
El área total del cuadrado es 1. Por tanto, el área amarilla del primer cuadrado es
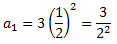
ya que el lado de los cuatro cuadrados es 1/2.
En el segundo cuadrado, el lado de los cuatro cuadrados pequeños es la mitad del lado de los cuatro cuadrados grandes, es decir, 1/4. Por tanto, el área amarilla es
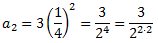
En el tercer cuadrado, el lado de los cuatro cuadrados pequeños es la mitad del lado de los cuatro cuadrados intermedios, es decir, 1/8. Por tanto, el área amarilla es
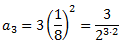
Si sumamos todos los términos de la sucesión tendremos el área total del cuadrado, que es 1. Así que
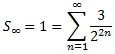
Nota: obsérvese que
-
El término general de la sucesión geométrica es $$a_n =\frac{3}{2^{2n}}$$
-
El primer término es \(a_1 = 3/4\) y la razón es \(r= 1/4\).
-
Aplicando la fórmula de la suma de todos los términos tenemos
$$ S_\infty = \frac{a_1}{1-r} =$$
$$ = \frac{3/4}{1-1/4} = 1 $$
Problema 28 
Según una leyenda, un rico brahmán ordenó a su sirviente,
Sisa, que creara un juego para que pudiera entretenerse. Sisa
le presentó el tablero de ajedrez y el brahmán quedó tan
satisfecho que le dejó escoger su recompensa. Así pues, le
pidió que le pagara con un grano de trigo por el primer casillero del
tablero, dos por el segundo, cuatro por el tercero, ocho por el
cuarto, etc. hasta llegar a los 64 casilleros.
-
Calcular a cuántos granos de trigo ascendía la recompensa.
-
Si en un 1kg hay aproximadamente 20.000 granos, ¿cuántos kilogramos de trigo obtuvo Sisa?
Ver solución
El número de granos en cada casillero corresponde con la los términos de la progresión geométrica

Queremos calcular la suma de los 64 primeros términos. Como la razón es r = 2 y el último término es \(a_{64}\),
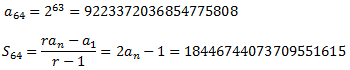
Aplicando una regla de 3, la recompensa asciende a unos 922 337 203 685 477 kg de trigo.
Problema 29 
A las 9 de la mañana, una persona cuenta a tres amigos un secreto.
Media hora después, cada uno de estos tres amigos cuenta el secreto
a otras tres personas. Media hora más tarde, cada uno de éstos cuenta
el secreto a otras tres personas y así sucesivamente.
Calcular cuántas
personas saben el secreto a las 9 de la noche suponiendo que cada persona
sólo cuenta el secreto a otras tres personas y a nadie más durante el día
y que ninguno ha recibido la información varias veces.
Ver solución
Construimos una sucesión en la que cada término será el número de personas nuevas que conocen el secreto:
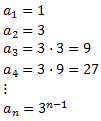
Es una sucesión geométrica de razón r = 3. Cada media hora se extiende el secreto y el tiempo total son 12h, es decir, 24 medias horas. Entonces, queremos calcular la suma de los 24 primeros términos:
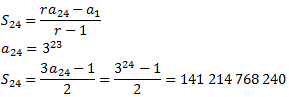
Es decir, lo sabría el mundo entero ya que en el mundo hay unos 8.000 millones de personas (cifra del 2023).
Problema 30 
Encontrar el valor de n para que se cumpla la igualdad
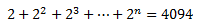
Ver solución
Consideremos la progresión geométrica de razón 2 y cuyo primer término es 1. Su término general es
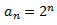
buscamos n tal que
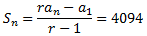
Como la razón es r = 2,
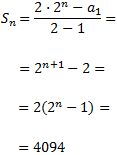
Finalmente, resolvemos la ecuación exponencial