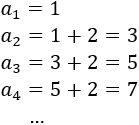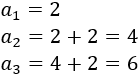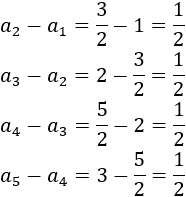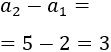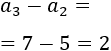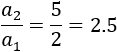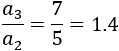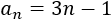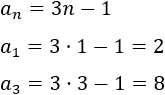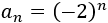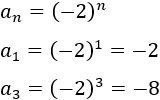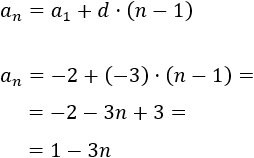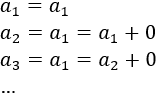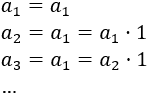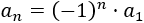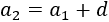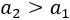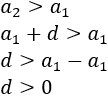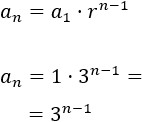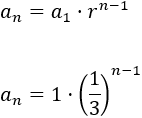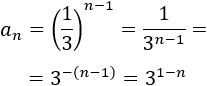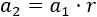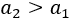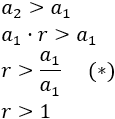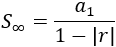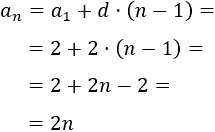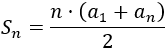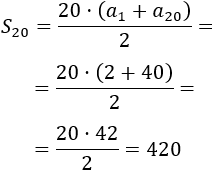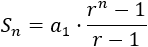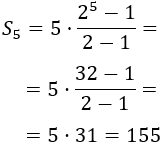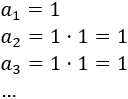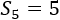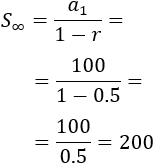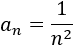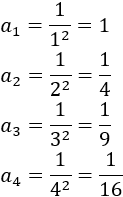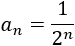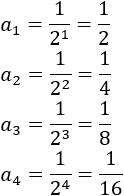Escoger la opción correcta en todas las preguntas.
Pregunta 1
El conjunto de números impares, {1, 3, 5, 7,...} puede considerarse como una progresión...
|
|
aritmética con diferencia \(d = 2\).
|
|
|
geométrica con razón \(r = 2\).
|
|
|
ni aritmética ni geométrica.
|
Razonamiento:
Mostrar
Es una sucesión aritmética con diferencia \(d = 2\) ya que cada término se obtiene sumando 2 al término anterior:
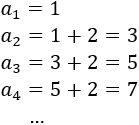
Pregunta 2
El conjunto de números {2, 4, 6} es una progresión...
|
|
aritmética con diferencia \(d = 3\).
|
|
|
geométrica con razón \(r = 2\) .
|
|
|
aritmética y finita.
|
Razonamiento:
Mostrar
Es una sucesión finita porque sólo consta de tres términos. Es aritmética con diferencia \(d = 2\):
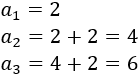
Pregunta 3
El conjunto de números racionales {1, 3/2, 2, 5/2, 3,... } es una progresión...
|
|
aritmética con diferencia \(d = 1/2\).
|
|
|
geométrica con razón \(r = 1/2\).
|
|
|
ni aritmética ni geométrica.
|
Razonamiento:
Mostrar
Si la sucesión es aritmética, la diferencia entre dos términos consecutivos debe ser contante. Lo comprobamos:
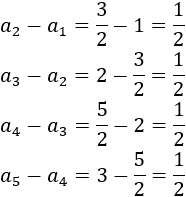
La diferencia se mantiene constante. Se trata de una sucesión aritmética con diferencia \(d = 1/2\).
Pregunta 4
La sucesión 2, 5, 7, 9, 10, 11,... es una sucesión...
|
|
aritmética.
|
|
|
geométrica.
|
|
|
ni aritmética ni geométrica.
|
Razonamiento:
Mostrar
No es aritmética porque la diferencia entre dos términos consecutivos no es constante. Por ejemplo, la diferencia entre el segundo y el primer término es
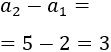
Mientras que la diferencia entre el tercer y el segundo término es
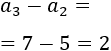
Tampoco es geométrica porque la razón entre términos consecutivos no es constante. Por ejemplo, la razón entre el segundo y el primer término es
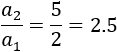
Mientras que la razón entre el tercer y segundo termino es
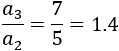
Pregunta 5
La sucesión 1, 5, 25, 125, 625,... es una sucesión...
|
|
aritmética con diferencia \( d = 5\).
|
|
|
geométrica con razón \(r = 5\).
|
|
|
ni aritmética ni geométrica.
|
Razonamiento:
Mostrar
No es aritmética porque la diferencia entre el segundo y el primer término es 4 y la diferencia entre el tercero y el segundo es 20.
Sin embargo, la razón entre términos consecutivos es constante e igual a 5.
Pregunta 6
Si el término general de una sucesión es
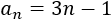
¿cuáles son el primer y el tercer término?
|
|
\(a_1 = -1\) y \(a_3 = 8\).
|
|
|
\(a_1 = 2\) y \(a_3 = 8\).
|
|
|
\(a_1 = 2\) y \(a_3 = -1\).
|
Razonamiento:
Mostrar
Sustituimos \(n = 1\) y \(n = 3\) para calcular el primer y el tercer término:
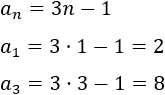
Pregunta 7
Si el término general de una sucesión es
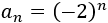
¿cuáles son el primer y el tercer término?
|
|
\(a_1 = -2\) y \(a_3 = -8\).
|
|
|
\(a_1 = 2\) y \(a_3 = 8\).
.
|
|
|
\(a_1 = -2\) y \(a_3 = 8\).
|
Razonamiento:
Mostrar
Sustituimos \(n = 1\) y \(n = 3\) para calcular el primer y el tercer término:
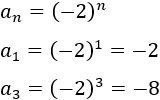
Pregunta 8
¿Cuál es el término general de la sucesión -2, -5, -8,...?
|
|
\(a_n = 3n-1\).
|
|
|
\(a_n = (-2)^n\) .
|
|
|
\(a_n = 1-3n\).
|
Razonamiento:
Mostrar
Es fácil ver que se trata de una sucesión aritmética con diferencia \(d = -3\). Como el primer término es \(a_1 = -2\), el término general es
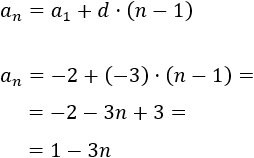
Pregunta 9
Una sucesión es estrictamente creciente cuando...
|
|
\( a_n > a_{n+1}\).
|
|
|
\(a_n < a_{n+1}\).
|
|
|
\( a_n \leq a_{n+1}\).
|
Razonamiento:
Mostrar
Que sea estrictamente significa que el signo debe ser > ó <, así que la tercera opción queda descartada.
Una sucesión es creciente cuando cada término es mayor que el término que le precede, lo que matemáticamente se escribe como
$$ a_n < a_{n+1} $$
O bien, como
$$ a_{n+1} > a_n $$
Pregunta 10
¿Cuándo se dice que una sucesión es alternada?
|
|
Cuando no es aritmética ni geométrica.
|
|
|
Cuando todos los términos tienen el mismo signo.
|
|
|
Cuando el signo de cada término es distinto al signo del término que le precede.
|
Razonamiento:
Mostrar
La tercera opción es la correcta por ser la propia definición de sucesión alternada.
La primera opción no es cierta ya que una sucesión puede ser no aritmética y no geométrica sin ser alternada. Un ejemplo de ello es la sucesión de Fibonacci: 1, 1, 2, 3, 5, 8, 13, ...
También, si la razón de una sucesión geométrica es negativa, la sucesión es alternada.
Pregunta 11
¿Cuándo se dice que una sucesión es constante?
|
|
Cuando no es aritmética ni geométrica.
|
|
|
Cuando no es estrictamente creciente ni estrictamente decreciente.
.
|
|
|
Cuando el signo de cada término es distinto al signo del término que le precede.
|
Razonamiento:
Mostrar
Una sucesión es constante cuando todos sus términos son iguales.
La primera opción no es la correcta porque una sucesión constante puede considerarse como aritmética con diferencia \(d = 0\) o como geométrica con razón \(r = 1\).
La tercera opción tampoco es la correcta porque es la definición de sucesión alternada.
Pregunta 12
Si una sucesión es aritmética y constante, entonces...
|
|
su diferencia es \(d = 0\).
|
|
|
su diferencia es \(d = 1\).
|
|
|
su diferencia es negativa (\(d < 0\)).
|
Razonamiento:
Mostrar
Cada término puede escribirse como el anterior más \(d = 0\):
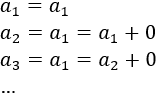
Pregunta 13
Si una sucesión es geométrica y constante, entonces...
|
|
su razón es \(r = 0\).
|
|
|
su razón es \(r = 1\).
|
|
|
su razón es negativa (\(r < 0\)).
|
Razonamiento:
Mostrar
Cada término puede escribirse como el anterior por \(r = 1\):
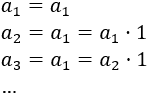
Pregunta 14
La sucesión cuyo término general es
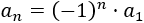
es una sucesión...
|
|
creciente.
|
|
|
decreciente.
|
|
|
alternada.
|
Razonamiento:
Mostrar
Es una sucesión alternada porque el factor \((-1)^n\) es positivo cuando \(n\) es par y negativo cuando \(n\) es impar.
Pregunta 15
Si una progresión es aritmética y estrictamente creciente (\(a_{n+1}> a_n\)), su diferencia...
|
|
siempre es positiva (\(d >0\)).
|
|
|
siempre es negativa (\(d < 0\)).
|
|
|
puede ser positiva o negativa.
|
Razonamiento:
Mostrar
Sea \(d\) la diferencia de la sucesión. Entonces, si el primer término es \(a_1\), el segundo es
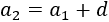
Como la sucesión es estrictamente creciente,
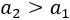
Por tanto,
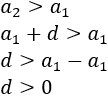
La diferencia es siempre positiva.
Pregunta 16
El término general de la sucesión creciente \(a_1 = 1\), \(a_2 = 3\), \(a_3 = 9\),... es...
|
|
\( a_n = 3^n\)
|
|
|
\( a_n = 3^{n-1}\)
|
|
|
\(a_n = 3^{n+1}\)
|
Razonamiento:
Mostrar
Como es una sucesión geométrica con primer término \(a_1 =1\) y con razón \(r = 3\), su término general es
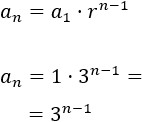
Pregunta 17
El término general de la sucesión decreciente \(a_1 = 1\), \(a_2 = 1/3\), \(a_3 = 1/9\),... es...
|
|
\( a_n = \left(\frac{1}{3} \right)^n\)
|
|
|
\( a_n = \left(\frac{1}{3} \right)^{n+1} \)
|
|
|
\(a_n = 3^{1-n}\)
|
Razonamiento:
Mostrar
Como es una sucesión geométrica con primer término \(a_1 =1\) y con razón \(r = 1/3\), su término general es
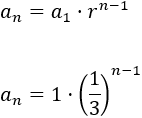
Si operamos un poco, obtenemos la fórmula de la tercera opción:
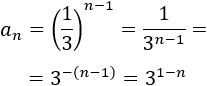
Pregunta 18
Si una progresión de números positivos es geométrica y estrictamente creciente (\(a_{n+1}> a_n\)), su razón...
|
|
siempre es positiva (\(r > 0\)).
|
|
|
siempre es negativa (\(r < 0\)).
|
|
|
siempre es mayor que la unidad (\(r > 1\)).
|
Razonamiento:
Mostrar
Sea \(r\) la razón de la sucesión. Entonces, si el primer término es \(a_1\), el segundo es
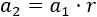
Como la sucesión es estrictamente creciente,
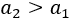
Por tanto,
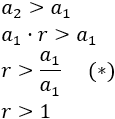
La razón es mayor que la unidad.
Nota: el paso (*) no es cierto si \(a_1\) es positivo.
Pregunta 19
En una sucesión geométrica con razón \(-1< r < 0\), ¿cuándo se puede calcular la suma de todos los términos que la conforman?
|
|
Siempre.
|
|
|
Nunca.
|
|
|
Cuando es finita.
|
Razonamiento:
Mostrar
Independientemente del número de términos, si la razón es \(-1< r < 1\), la suma siempre puede calcularse mediante la fórmula
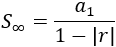
Pregunta 20
Si consideramos 2 como el primer número par, ¿cuánto suman los 20 primeros números pares?
|
|
Suman 320.
|
|
|
Suman 246.
|
|
|
Suman 420.
|
Razonamiento:
Mostrar
La sucesión de los números pares es aritmética con diferencia \(d = 2\). Como el primero de ellos es 2, el término general es
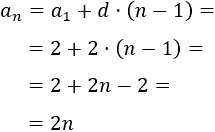
Así que el término \(a_{20}\) es 40.
La suma de los \(n\) primeros términos es
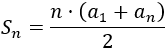
Por tanto, la suma de los 20 primeros pares es
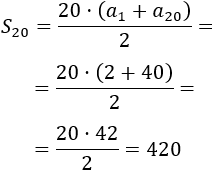
Pregunta 21
La suma de los 5 primeros términos de la sucesión geométrica con razón \(r = 2\) y primer término \(a_1 = 5\) es...
|
|
\( S_5 = 155\)
|
|
|
\( S_5 = 515\)
|
|
|
\( S_5 = 551\)
|
Razonamiento:
Mostrar
La fórmula para calcular la suma de los \(n\) primeros términos es
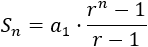
Por tanto,
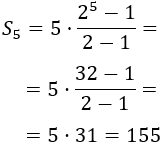
Pregunta 22
La suma de los 5 primeros términos de la sucesión geométrica con razón \(r = 1\) y primer término \(a_1 = 1\) es...
|
|
\( S_5 = 1\)
|
|
|
\( S_5 = 5\)
|
|
|
\( S_5 = 15\)
|
Razonamiento:
Mostrar
Como la razón es \(r = 1\), la sucesión es constante:
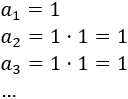
Por tanto, la suma de los 5 primeros términos es
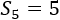
Pregunta 23
La suma de todos los términos de la sucesión geométrica con razón \( r = 0.5\) y primer término \(a_1 = 100\) es...
|
|
\( S_\infty = 2.401\)
|
|
|
\( S_\infty = 200\)
|
|
|
\( S_\infty = \infty \)
|
Razonamiento:
Mostrar
Como la razón es \(|r|< 1\), pueden sumarse todos los términos de la sucesión:
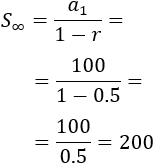
Pregunta 24
El término general de una sucesión es
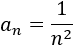
Esta sucesión...
|
|
es aritmética.
|
|
|
es geométrica.
|
|
|
no es aritmética ni geométrica.
|
Razonamiento:
Mostrar
Los primeros términos de la sucesión son
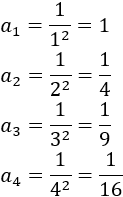
No es una sucesión geométrica ni aritmética.
Pregunta 25
El término general de una sucesión es
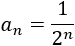
Esta sucesión...
|
|
es aritmética.
|
|
|
es geométrica.
|
|
|
no es aritmética ni geométrica.
|
Razonamiento:
Mostrar
Los primeros términos de la sucesión son
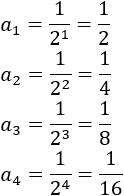
Se trata de una sucesión geométrica con razón \(r = 1/2\).
Enlace: Introducción a las progresiones, con ejemplos y problemas (PyE)