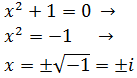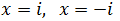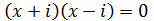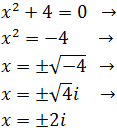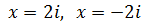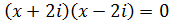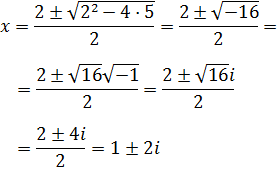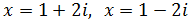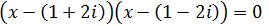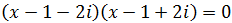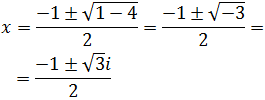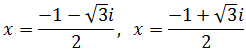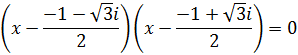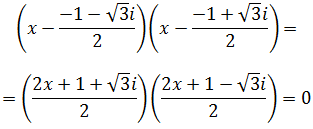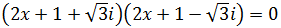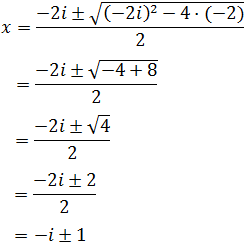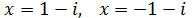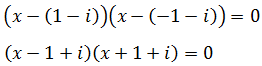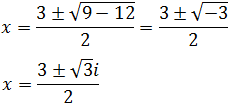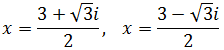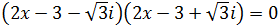Ecuaciones de segundo grado con soluciones complejas |
Contenido de esta página:
Introducción y método de resolución
-
6 ecuaciones resueltas
Introducción
Recordemos que dada la ecuación de segundo grado (o cuadrática)
$$ ax^2 + bx + c = 0 $$
Sus soluciones vienen dadas por la fórmula
$$ x = \frac{-b \pm \sqrt{b^2 -4ac}}{2a} $$
Llamamos discriminante al radicando de la fórmula anterior:
$$ \Delta = \sqrt{b^2 -4ac} $$
Es fácil ver que
-
Si \( \Delta > 0\), entonces las dos raíces son reales (el radicando de la fórmula es positivo).
-
Si \( \Delta = 0\), entonces la raíz de la fórmula vale 0 y, por tanto, sólo existe una solución que es real y de multiplicidad 2 (es una raíz doble).
-
Si \( \Delta < 0\), entonces las dos raíces son complejas y, además, una es el conjugado de la otra. Esto es, si una solución es \(x_1 = a+bi\), entonces, la otra solución es \( x_2 = a - bi\) (estamos suponiendo que \(a, b, c\) son reales).
En esta sección vamos a resolver ecuaciones de segundo grado cuyas soluciones son complejas (números imaginarios). Para las ecuaciones con raíces reales tenemos las secciones ecuaciones de segundo grado completas e incompletas.
Una vez obtengamos las soluciones, escribiremos una factorización de la ecuación. Es decir, la escribiremos como producto de dos polinomios de grado 1. Para esto, recordemos que si las soluciones de la ecuación
$$ ax^2 + bx + c = 0 $$
son \( x_1,\ x_2 \), entonces
$$ ax^2 + bx + c = a(x-x_1)(x-x_2) $$
Por lo que podemos escribir la ecuación como
$$ a(x-x_1)(x-x_2) = 0 $$
Siempre es posible escribir la ecuación en esta forma.
Finalmente, recordemos que la unidad imaginaria es
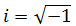
De esto modo, si tenemos la raíz cuadrada de un número negativo, -a, (a es el número en positivo), entonces
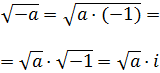
Recordemos también las potencias de i:
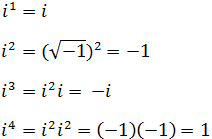
En general, las potencias son
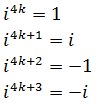
para cualquier entero k.
Enlace: más información sobre el producto de los números complejos.
6 Ecuaciones Resueltas
Ecuación 1
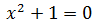
Ecuación 2
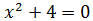
Ecuación 3
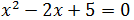
Ecuación 4
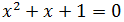
Ecuación 5
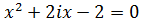
Ecuación 6
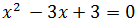

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.