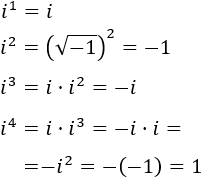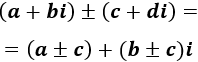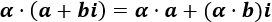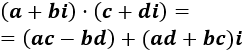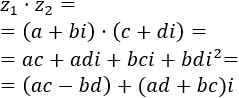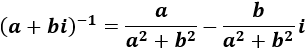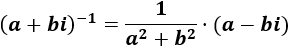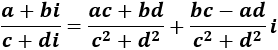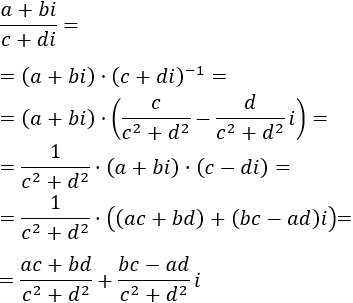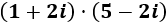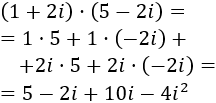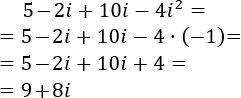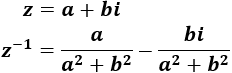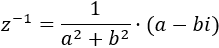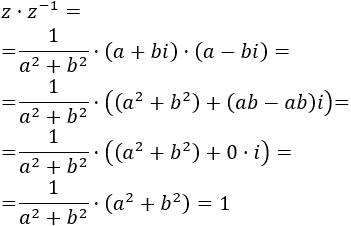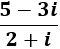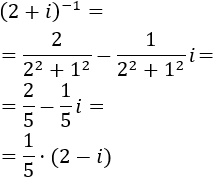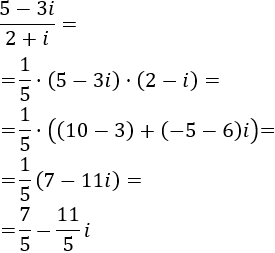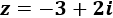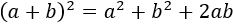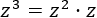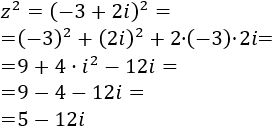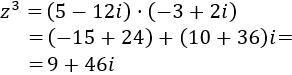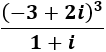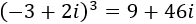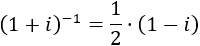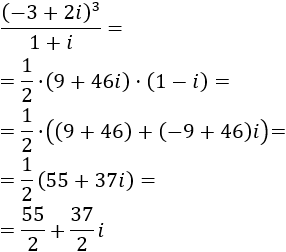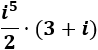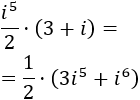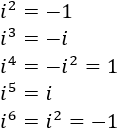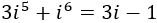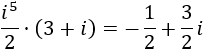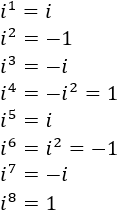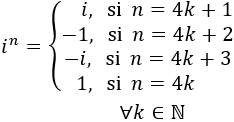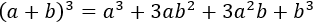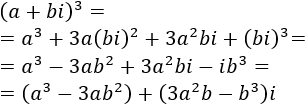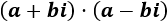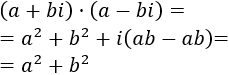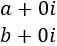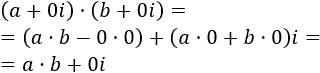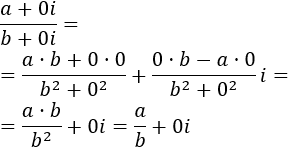Problema 1
Calcular el siguiente producto de complejos sin aplicar la fórmula:
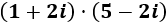
Ver solución
Multiplicamos los complejos como lo haríamos con un producto de binomios (cada sumando del primero por cada sumando del segundo):
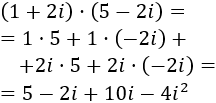
Escribimos \(i^2 = -1\):
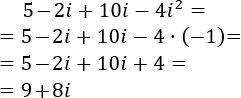
Problema 2
Comprobar que el producto de un complejo \(z\neq 0\) por su inverso \(z^{-1}\) es la unidad:
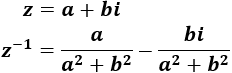
Ver solución
El inverso de \(z\) es
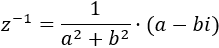
Calculamos el producto de los complejos (aplicando la fórmula):
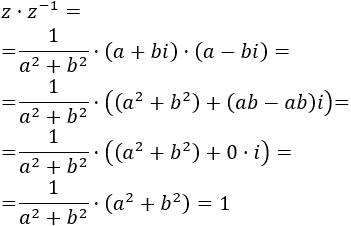
Problema 3
Calcular el siguiente cociente de complejos sin aplicar la fórmula:
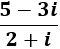
Ver solución
El inverso del denominador es
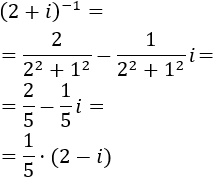
Calculamos el cociente de los complejos multiplicando el numerador por el inverso del denominador:
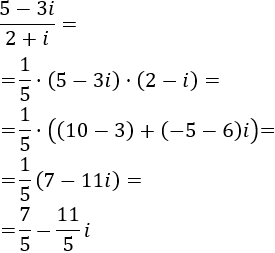
Problema 4
Calcular el cubo \(z^3\) del complejo
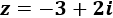
Ver solución
Como hemos visto, la forma binómica de los complejos nos permite trabajar con ellos como si fuesen los binomios de siempre. Así que podríamos aplicar la fórmula del cubo de una suma. No obstante, como normalmente los estudiantes no conocen la fórmula del cubo, usaremos la del cuadrado:
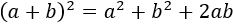
Para poder aplicarla, tenemos que escribir el cubo como el producto:
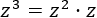
El cuadrado de \(z\) es
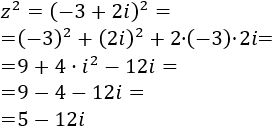
Así que su cubo es
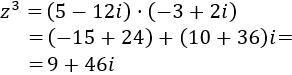
Problema 5
Calcular el siguiente cociente de complejos:
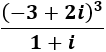
Ver solución
El cubo del numerador ya lo hemos calculado en el problema anterior:
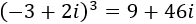
Calculamos el inverso del denominador:
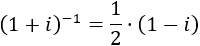
Por tanto, el cociente del problema es el producto de los complejos anteriores:
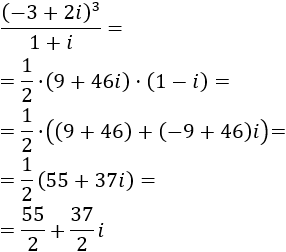
Problema 6
Calcular el siguiente producto de complejos:
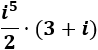
Ver solución
Calculamos el producto:
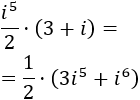
Calculamos las potencias de la unidad imaginaria:
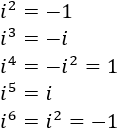
Por tanto,
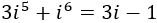
Así que el resultado final es
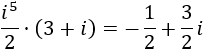
Problema 7
Calcular la potencia \(n-\)ésima de la unidad imaginaria, es decir, \(i^n\).
Ver solución
Las primeras potencias son
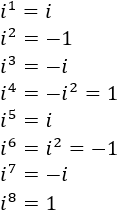
Por tanto, deducimos (y se demuestra por inducción sobre \(n\)) que la potencia \(n-\)ésima de \(i\) es
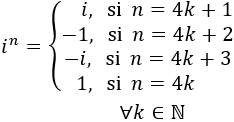
Problema 8
Obtener una fórmula para calcular el cubo de un complejo en forma binómica, es decir, para calcular \((a+bi)^3\).
Ver solución
La fórmula que tenemos para los reales es
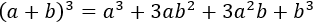
Por tanto, si escribimos \(bi\) en lugar de \(b\), tenemos
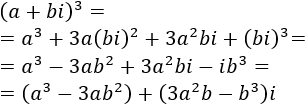
Problema 9
Calcular el producto de un complejo por su conjugado, es decir,
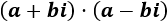
Ver solución
El resultado obtenido es el cuadrado del módulo del complejo:
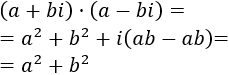
Problema 10
Comprobar que el producto y el cociente de complejos no afecta al producto y al cociente de reales. Es decir, comprobar que el resultado del producto y del cociente de los números reales no cambia si se consideran como números complejos (con parte imaginaria nula).
Ver solución
Sean \(a\) y \(b\) dos números reales. Para considerarlos como complejos, los escribimos como
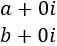
El producto de estos complejos es
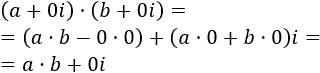
Por tanto, coincide con \(a·b\).
Si \(b\neq 0\), entonces el cociente de los complejos es
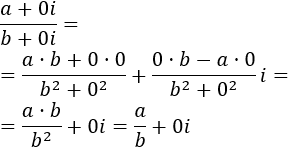
Por tanto, coincide con \(a/b\).


Producto y cociente de números complejos -
© -
matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.