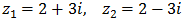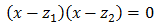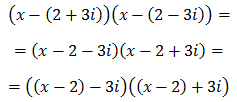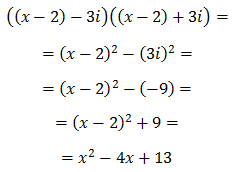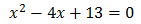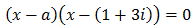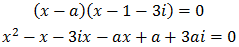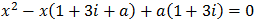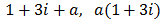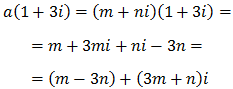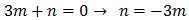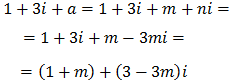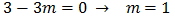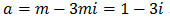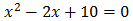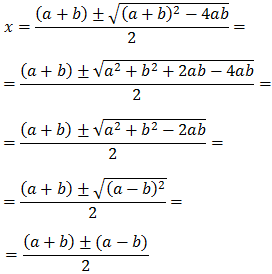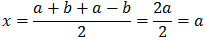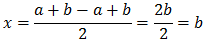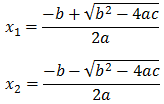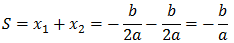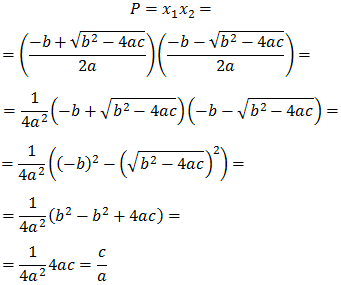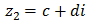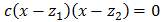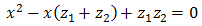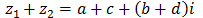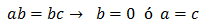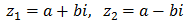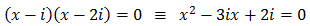Contenido de esta página:

• Obtención de ecuaciones a partir de sus soluciones complejas

• Obtención de ecuaciones a partir de la suma y producto de sus soluciones

• Demostración de propiedades teóricas sobre las soluciones

• Ecuaciones con coeficientes reales y complejos

Enlaces relacionados:

• Ecuaciones de segundo grado completas

• Ecuaciones de segundo grado incompletas

• Ecuaciones de segundo grado con raíces complejas

Introducción

En esta página demostraremos algunas propiedades teóricas de las ecuaciones de segundo grado y las aplicaremos para resolver problemas. Las propiedades son las siguientes:

• Suma de las raíces:

  Si x₁ y x₂ son las soluciones de la ecuación de segundo grado

  $$ ax^2 + bx + c = 0 $$

  Entonces, su suma, S, es

  $$ S = x_1 + x_2 = \frac{-b}{a} $$

  Demostración: problema 5.

• Producto de las raíces:

  Si x₁ y x₂ son las soluciones de la ecuación de segundo grado

  $$ ax^2 + bx + c = 0 $$

  Entonces, su producto, P, es

  $$ P = x_1 \cdot x_2 = \frac{c}{a} $$

  Demostración: problema 5.

• Factorización de la ecuación

  $$ ax^2 + bx + c = 0 $$

  Si x₁ y x₂ son las soluciones de la ecuación anterior, entonces, podemos escribir la ecuación en forma factorizada como

  $$ a(x-x_1)(x-x_2) = 0 $$

  Notemos que las soluciones no dependen del factor a, pero lo escribimos ya que así se tiene que

  $$ a(x-x_1)(x-x_2) = ax^2 + bx + c $$

  Por tanto, conociendo las soluciones podemos calcular la ecuación.

• Otra forma de obtener la ecuación a partir de las soluciones es la siguiente:

  Una ecuación de segundo grado cuyas raíces son los números x₁ y x₂ es

  $$ x^2 - Sx + P = 0 $$

  siendo S la suma de las raíces y P el producto, es decir,

  $$ S = x_1 + x_2 $$

  $$ P = x_1 \cdot x_2 $$

  Demostración: problema 4.

• Si los coeficientes de una ecuación de segundo grado son reales, es decir, si a, b y c son reales, entonces:

  • Sus dos raíces son reales

  • o bien, sus dos raíces son complejas. En este caso, además, si una de las raíces es el complejo

    $$ x_1 = a+bi $$

    Entonces, la otra solución es necesariamente

    $$ x_2 = a-bi = \overline{x_1} $$

    Es decir, es el conjugado de la otra raíz.

    Demostración: problema 7.

Problemas Resueltos

Problema 1

Escribir una ecuación de segundo grado cuyas soluciones son los complejos

$$ 2 \pm 3i $$

¿Sus coeficientes son reales o complejos?

Problema 2

Una ecuación de segundo grado con coeficientes reales puede tener alguna solución compleja, por ejemplo,

$$ x^2 +x + 1 = 0 $$

tiene los coeficientes reales y sus dos soluciones son complejas.

Encontrar, si es posible, una ecuación de segundo grado con coeficientes complejos pero con raíces reales.

Problema 3

Escribir una ecuación de segundo grado cuyos coeficientes sean reales y una de sus soluciones sea 1 + 3i.

¿Cuál es la otra solución? Razonar la respuesta.

Problema 4

Encontrar las raíces de la ecuación

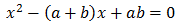
Problema 5

Demostrar que si x₁ y x₂ son las soluciones de la ecuación de segundo grado

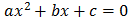
Entonces,

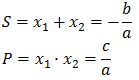
Problema 6

Encontrar la ecuación de segundo grado cuyas soluciones suman 5 y cuyo producto es -24.

Problema 7

Demostrar que si

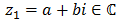
es una solución de una ecuación de segundo grado con coeficientes reales, entonces, su conjugado,

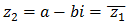
es la otra solución de la ecuación.

Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.