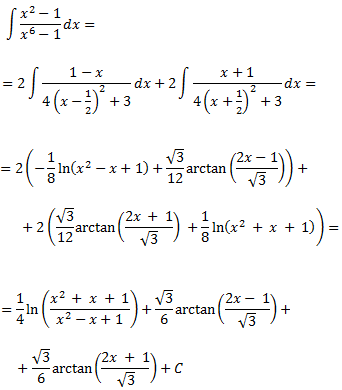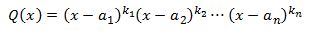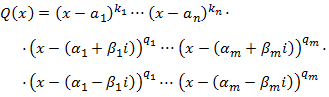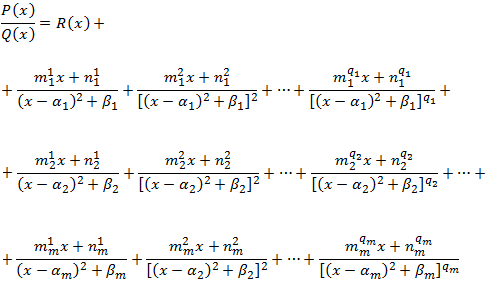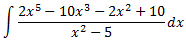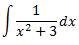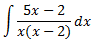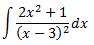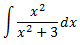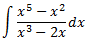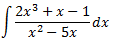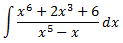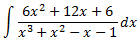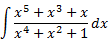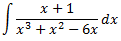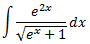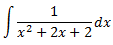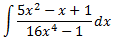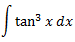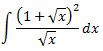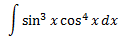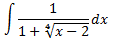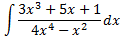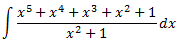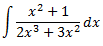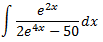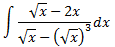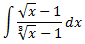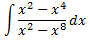Supongamos que tenemos la integral
$$\int{\frac{P(x)}{Q(x)}}dx$$
donde \(P(x)\) y \(Q(x)\) son los polinomios del numerador y denominador,
respectivamente.
Distinguimos los siguientes casos:
-
grado( P ) \(\geq\) grado( Q ): efectuamos la división de los polinomios.
-
grado( P ) < grado( Q ):
En este caso, aplicaremos el Teorema Fundamental del Álgebra. Subcasos:
Caso 1: grado de P mayor o igual que el de Q
En este caso, el método consiste en efectuar una división polinómica para poder descomponer la integral.
Antes de efectuar la división de polinomios tenemos que factorizar los polinomios del numerador y denominador (expresarlos como productos de (x - raíz) ) porque si tenemos algún mismo factor en el numerador y denominador podemos quitarlos (simplificar).
Si tenemos la integral
$$\int{\frac{P(x)}{Q(x)}}dx$$
Al efectuar la división tendremos que
$$P(x) = Q(x) \cdot C(x) + R(x)$$
siendo C(x) el polinomio cociente y R(x) el polinomio resto de la división.
Si dividimos la expresión por Q(x) obtenemos
$$\frac{P(x)}{Q(x)} = C(x) + \frac{R(x)}{Q(x)}$$
De este modo, aplicando las propiedades de las integrales, habremos descompuesto la integral en la suma de dos integrales:
$$\int{\frac{P(x)}{Q(x)}}dx =\int{C(x)}dx + \int{\frac{R(x)}{Q(x)}}dx$$
Caso 2: grado de P menor que el de Q
Caso (a): todas las raíces de Q son reales
Podemos factorizar el polinomio \(Q\) y escribirlo como
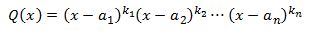
donde cada \(a_i\) son las raíces (reales) de \(Q\) y \(k_i\) es el grado de multiplicidad
de la raíz \(a_i\), esto es, el número de veces que se repite la raíz.
Nota: estamos suponiendo, por comodidad, que los polinomios son mónicos, es decir, que tienen 1 como coeficiente director.
Si es necesario, para buscar las raíces de los polinomios podemos aplicar la regla de Ruffini.
Según el Teorema Fundamental del Álgebra, podemos expresar el cociente \(P(x)/Q(x)\) como una suma de cocientes a los que denominamos
fracciones simples:

donde los términos \(b_i^j\) son reales y cuyos valores desconocemos.
Tendremos que buscarlos dando valores a x.
Caso (b): NO todas las raíces de Q son reales
Factorizamos el denominador, \(Q\), obteniendo una expresión como la siguiente
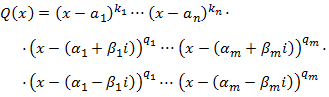
donde \(a_i\) son las raíces reales de \(Q\) con multiplicidades \(k_i\) y
\(\alpha_j + i\beta_j\) son las raíces complejas con multiplicidades \(q_j\).
Nota: si un complejo
\(z=\alpha + i\beta\) es raíz de un polinomio, entonces, su conjugado \(\overline{z}=\alpha_j - i\beta_j\) también lo es y, además, tienen la misma multiplicidad.
Por el Teorema Fundamental del Álgebra,
podemos escribir el cociente \(P(x)/Q(x)\) como sigue
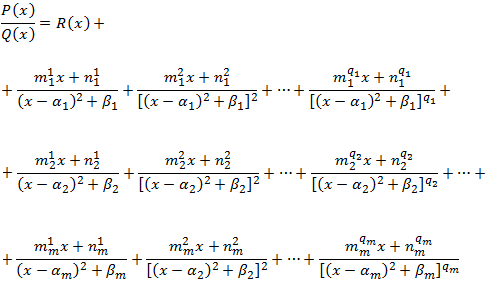
donde \(m_i^j\) y
\(n_i^j\) son constantes reales que desconocemos.
Nota: no debe confundirse el suníndice \(m\) (número de raíces complejas del polinomio) con las constantes \(m_i^j\).
El polinomio \(R(x)\) es la suma de fracciones simples asociada a las raíces reales que ya sabemos cómo escribir (caso anterior) y que hemos omitido para simplificar la notación.
Obsérvese que se trata del mismo procedimiento aunque las fracciones simples asociadas a las raíces complejas tienen otra forma.
Debemos calcular las constantes \(m_i^j\) y \(n_i^j\). Para ello, multiplicamos la igualdad anterior por la factorización de \(Q\) y damos valores
a \(x\) para obtener un sistema lineal de ecuaciones. Una vez calculadas, podremos expresar la integral como una suma de integrales simples.
Integral 1
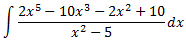
Solución
Como el grado del polinomio del numerador es mayor que el del denominador, dividimos los polinomios:
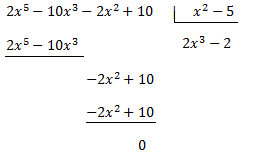
Por tanto, podemos escribir el dividendo como el producto del divisor y del cociente (más el resto, que es 0)
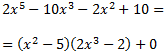
Dividiendo entre el polinomio cociente, podemos escribir la fracción de polinomios como un polinomio de grado 3:
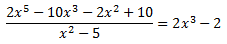
De este modo, la integral es
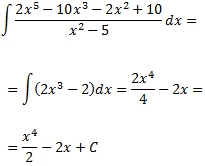
Integral 2
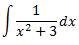
Solución
El grado del polinomio del denominador es mayor que el del numerador, así que no podemos dividir los polinomios.
En un principio, aplicaríamos el Teorema Fundamental del Álgebra pero, por la forma del integrando, podemos transformarlo en la derivada de un arctan. Operamos un poco:
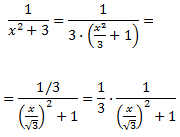
Por tanto, la integral que queda es inmediata:
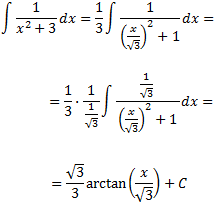
Integral 3
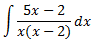
Solución
Al ser el grado del polinomio del denominador mayor que el del numerador, aplicamos el Teorema Fundamental del Álgebra para expresar el cociente como una suma de fracciones simples:
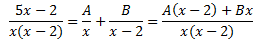
Para obtener las constantes A y B, damos valores a x en la igualdad anterior. Es suficiente
con comprobar que los numeradores sean iguales ya que los denominadores son iguales:
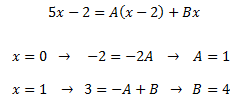
Luegopodemos escribir la integral como una suma y, aplicando sus propiedades, como una suma de
integrales:
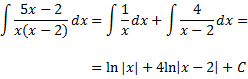
Nota: el argumento de un logaritmo debe ser un valor
absoluto, excepto que éste sea siempre positivo (por ejemplo, si es \(x^2\)).
Integral 4
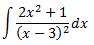
Solución
Desarrollamos el denominador:
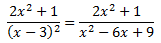
Como los grados de los polinomios son el mismo, dividimos los polinomios:
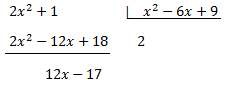
Escribimos el dividendo como el producto del divisor por el cociente más el resto:
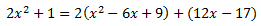
Al dividir en ambos lados por el divisor se obtiene una suma:
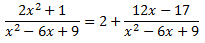
Escribimos la integral como la suma de la integral de una constante y la integral de un cociente de polinomios:
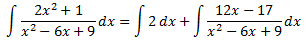
La primera de las integrales es inmediata. La segunda es un cociente de polinomios. Puesto que el grado del denominador es mayor, buscamos sus raíces para aplicar el Teorema Fundamental del Álgebra y expresar el cociente como suma de fracciones simples. Ya sabemos que
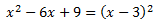
Es decir, tenemos una raíz real doble y ninguna raíz compleja. Así pues, la
descomposición en fracciones simples es de la forma
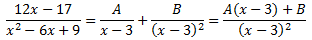
Para obtener las constantes, damos valores a x en la siguiente igualdad
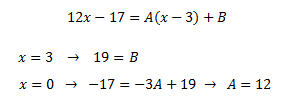
Esta descomposición nos permite descomponer la integral en una suma de integrales:

Ambas integrales son inmediatas:
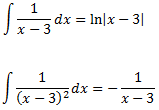
Luego el resultado de la integral inicial es
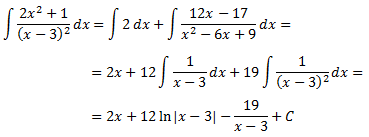
Integral 5
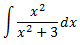
Solución
Como el grado de los polinomios del numerador y del denominador son el mismo, dividimos los polinomios:
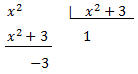
Por tanto, podemos escribir el numerador como
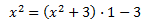
De donde obtenemos la descomposición del cociente en una suma:
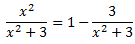
Escribimos la integral como una suma de integrales:
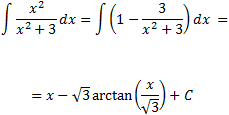
La segunda integral la hemos resuelto en el ejercicio 2.
Integral 6
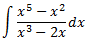
Solución
Nota: podemos simplificar el integrando:
$$\frac{^5-x^2}{x^3-2x} = \frac{x^4-x}{x^2-2}$$
Aunque nosotros no lo hemos hecho porque en este procedimiento no cambia demasiado.
Como el grado del polinomio del numerador es mayor que el del denominador, dividimos los polinomios:
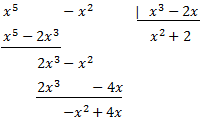
Esto nos permite escribir el cociente como una suma de fracciones más simples:
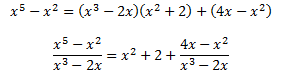
Así, podemos descomponer la integral como una suma de integrales:
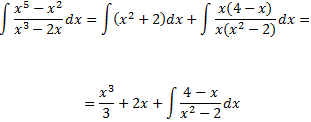
El grado del polinomio del denominador de la integral que queda es mayor que el del numerador. Buscamos las raíces del denominador:
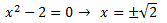
Como las raíces son reales, por el Teorema Fundamental del Álgebra, podemos escribir el cociente como una suma de dos fracciones simples:
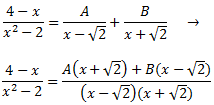
Damos valores a x en la igualdad para determinar las constantes A y B:
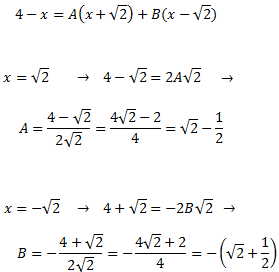
Por tanto, la descomposición del cociente es
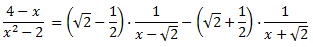
Luego el resultado de la integral inicial es
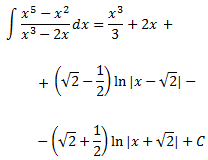
Integral 7
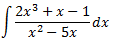
Solución
Como el grado del polinomio del numerador es mayor que el del denominador, dividimos los polinomios:
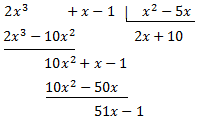
Por tanto, el numerador se puede escribir como
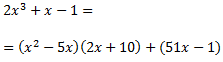
Dividiendo entre el divisor la igualdad anterior, el cociente de los polinomios se puede escribir como la siguiente suma:
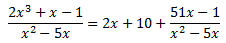
Así, podemos expresar la integral como la suma
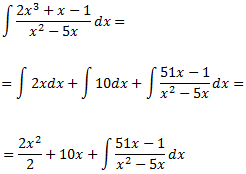
En la integral que queda, el grado del polinomio del denominador es mayor que el del numerador. Buscamos las raíces del denominador para descomponer la fracción en fracciones simples:
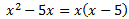
Al ser reales las raíces (0 y 5), por el Teorema Fundamental del Álgebra, el cociente se puede escribir como una la suma
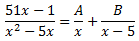
Para obtener los valores de las constantes A y B, damos valores a x en la igualdad:
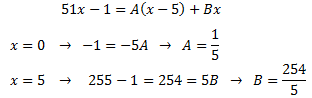
Por tanto, la integral puede descomponerse como sigue
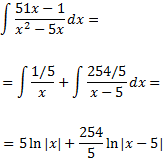
Luego el resultado de la integral inicial es
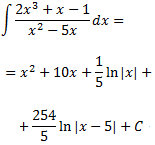
Integral 8 (dificultad alta)
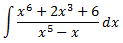
Solución
Como el grado del polinomio del numerador es mayor que el del denominador, dividimos los polinomios:
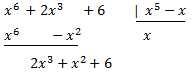
De donde se deduce la siguiente descomposición del dividendo:
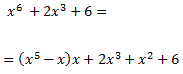
Luego la fracción del integrando puede escribirse como una suma:
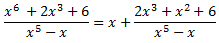
Lo que permite escribir la integral como la suma de dos integrales:
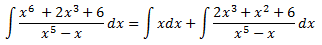
La primera integral es inmediata. Calculemos la segunda:
Al ser el grado del denominador mayor que el del numerador, buscamos las raíces del denominador para aplicar el Teorema Fundamental del Álgebra:
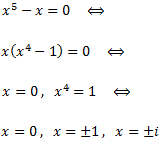
Por tanto, tenemos 3 raíces reales y dos raíces complejas.
Descomponemos la fracción en fracciones simples
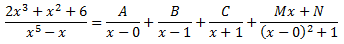
Es decir,
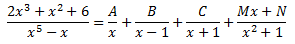
Operando se obtiene la igualdad
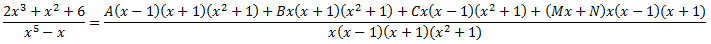
Calculamos las cinco constantes A, B, C, M y N dando valores a x en la igualdad
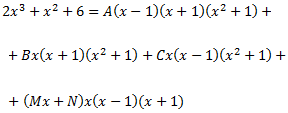
Utilizaremos \(x=1\), \(x=-1\), \(x=0\), \(x=2\) y \(x=-2\):
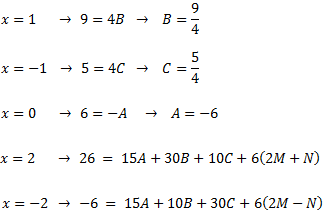
Para calcular las constantes \(M\) y \(N\), debemos resolver un sistema de ecuaciones lineales cuya solución es \(M=5/2\) y \(N=1\).
Luego las constantes son
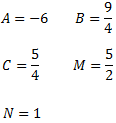
Con lo que la descomposición del cociente es
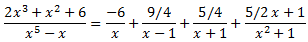
De este modo, la integral se descompone en la suma de otras cuatro integrales más sencillas:
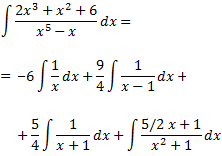
Las tres primeras integrales son inmediatas. Calculemos la cuarta:
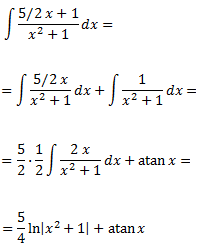
Con todo, el resultado de la integral inicial es
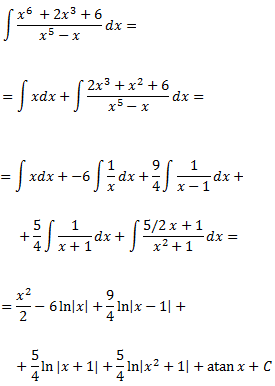
Integral 9
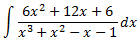
Solución
El grado del polinomio del denominador es mayor que el del numerador. Aplicamos la regla de Ruffini
para calcular las raíces del denominador.
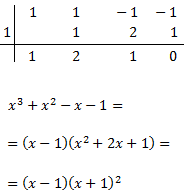
Ahora factorizamos el numerador para intentar simplificar la fracción:
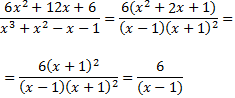
Por tanto, la integral que queda es inmediata:
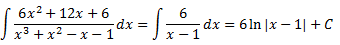
Integral 10
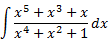
Solución
En realidad, se trata de una integral inmediata ya que si factorizamos los polinomios podemos simplificar el integrando
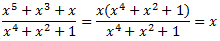
Por tanto, el resultado de la integral es
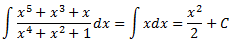
Integral 11
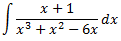
Solución
Como el grado del polinomio del denominador es mayor que el del numerador, descomponemos la fracción del integrando en una suma.
Para ello, buscamos las raíces del denominador:
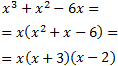
Todas las raíces son reales y simples. Por el Teorema Fundamental del Álgebra, podemos escribir el cociente como
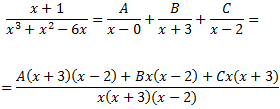
Damos valores a x en la siguiente igualdad para determinar las constantes:
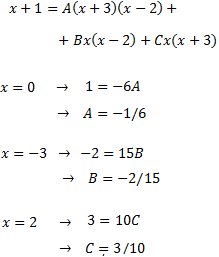
Por tanto, la descomposición de la fracción es

Finalmente, tenemos
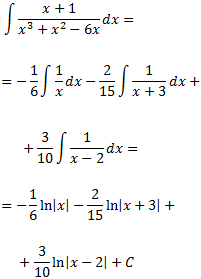
Integral 12
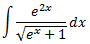
Solución
Al aplicar el cambio de variable
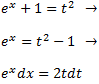
la integral queda como
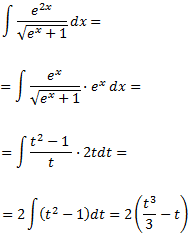
Como ya tenemos el resultado de la integral, deshacemos el cambio de variable. Primero despejamos
t:
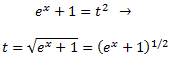
Obteniendo
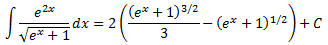
Integral 13
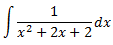
Solución
El grado del polinomio del numerador es mayor que el del denominador. Calculamos las raíces del polinomio del denominador:
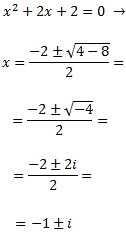
Por el Teorema Fundamental del Álgebra, podemos expresar el cociente como
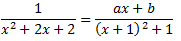
Damos valores a x para calcular las constantes a y b:
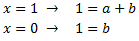
La solución del sistema anterior es
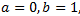
Luego
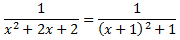
Nota: el resultado obtenido es evidente y puede obtenerse
directamente sin necesidad de aplicar el teorema. Pero lo hacemos así
para seguir el algoritmo de resolución.
La integral es inmediata por ser la derivada de un arctan:
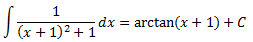
Integral 14
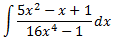
Solución
El grado del polinomio del denominador es mayor que el del denominador.
Buscamos las raíces del denominador:
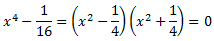
Las raíces son
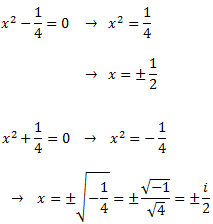
Como tenemos raíces reales y complejas, por el Teorema Fundamental del Álgebra, podemos escribir el cociente como
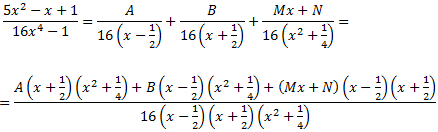
Nota: al no ser el denominador un polinomio mónico (coeficiente director 1), escribimos en el denominador de las fracciones simples su coeficiente director.
Para obtener las constantes, damos valores a x en la igualdad
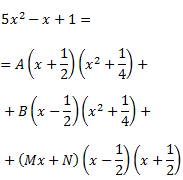
Para facilitar los cálculos, comenzamos dando los valores que son raíces (así obtenemos ceros):
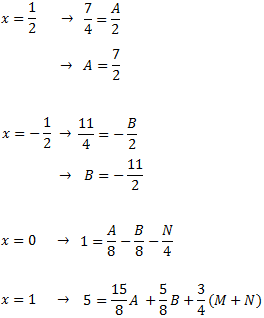
Resolvemos el sistema de ecuaciones. Por tanto, las cuatro constantes son
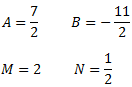
Por tanto, la descomposición de la fracción es
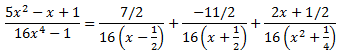
Lo que nos permite descomponer la integral inicial en una suma de integrales:
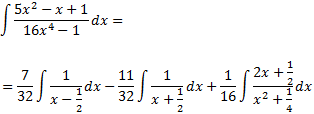
Las dos primeras integrales son inmediatas:
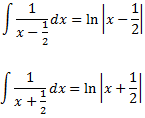
Calculamos la tercera integral convirtiendo el integrando en la suma de las derivadas de un arctan y de un ln
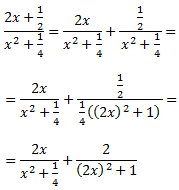
Cuya integral es
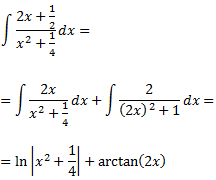
Luego el resultado de la integral inicial es
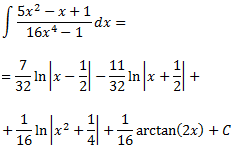
Integral 15
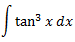
Solución
Hemos clasificado esta integral como racional ya que si aplicamos el cambio de variable
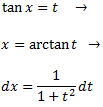
Obtenemos la integral
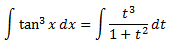
Como el grado del polinomio del numerador es mayor que el del denominador, dividimos los polinomios:
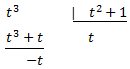
De donde se obtiene
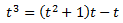
Dividimos entre t:
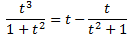
Finalmente, calculamos la integral y deshacemos el cambio de variable:
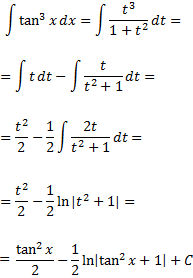
Integral 16
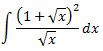
Solución
En realidad, esta integral encaja más en la sección de integración por sustitución. No obstante, el integrando es una fracción.
Aplicamos el cambio de variable
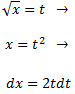
Y calculamos la integral resultante
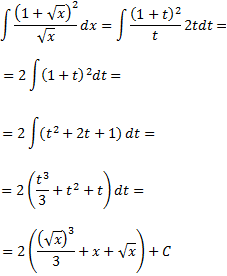
Integral 17
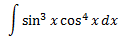
Solución
Al cambio de variable siguiente, el integrando es una función racional:
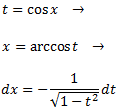
Además,
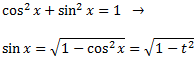
Resolvemos la integral:
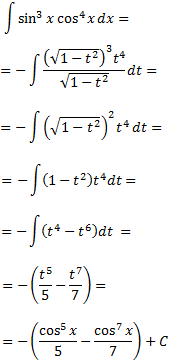
Integral 18
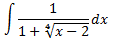
Solución
Aplicamos el cambio de variable
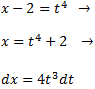
Y obtenemos una integral racional
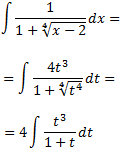
Como el grado del polinomio del numerador es mayor que el del denominador, dividimos los polinomios:
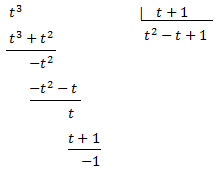
De donde obtenemos
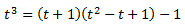
Lo que nos permite escribir el cociente de polinomios como una suma:
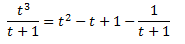
Luego la integral es
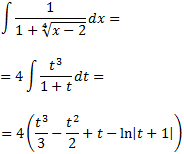
Deshacemos el cambio de variable

Por tanto,
Integral 19
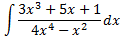
Solución
Como el grado del polinomio del denominador es mayor que el del numerador, buscamos las raíces del denominador:
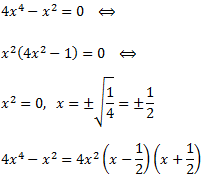
Las cuatro raíces son reales. Por el Teorema Fundamental del Álgebra, podemos descomponer la fracción en fracciones simples.
A diferencia del ejercicio 14, haremos que el polinomio del denominador sea mónico (coeficiente director 1) escribiendo el 4 en el numerador en forma de fracción 1/4:
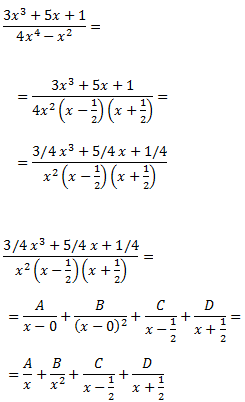
De donde se obtiene la igualdad
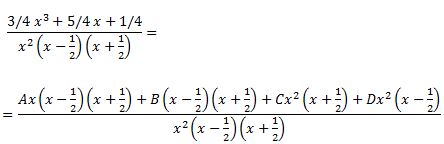
Para calcular las constantes A, B, C y D, damos
valores a x al igualar los numeradores
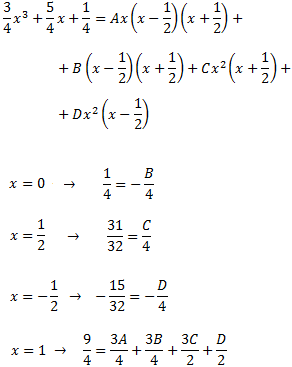
Resolvemos el sistema de ecuaciones lineales cuya solución es:
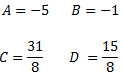
Por tanto, tenemos la siguiente descomposición en fracciones simples:
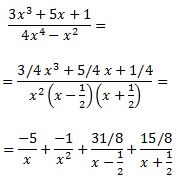
Esto permite descomponer la integral en una suma de integrales inmediatas:
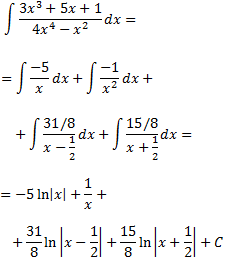
Integral 20
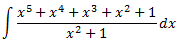
Solución
Como el grado del polinomio numerador es mayor que el del denominador, dividimos los polinomios:
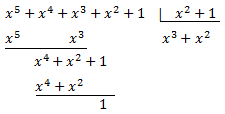
Por tanto, el dividendo es
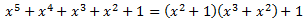
Al dividir la expresión anterior, se obtiene una descomposición de la fracción:
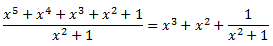
Así, podemos descomponer la integral en una suma de integrales inmediatas:
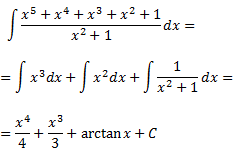
Integral 21
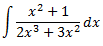
Solución
Buscamos las raíces del denominador:
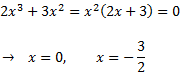
Escribimos el denominador en forma factorizada:
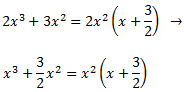
Por el Teorema Fundamental del Álgebra, podemos escribir el cociente como suma de fracciones simples (a diferencia del ejercicio 14, haremos el denominador mónico):
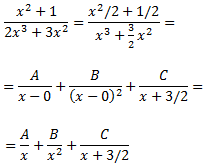
Al sumar las fracciones, se obtiene la igualdad
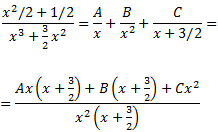
Damos valores a x en la siguiente igualdad para obtener las constantes A, B y C:
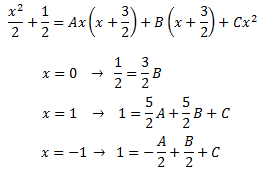
Resolvemos el sistema de ecuaciones lineales cuya solución es:
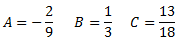
Como
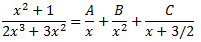
podemos escribir la integral como una suma:
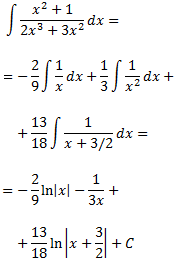
Integral 22
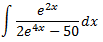
Solución
Aplicamos el siguiente cambio de variable:
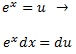
La integral resultante es
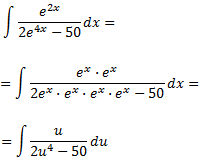
Calculamos las raíces del denominador:
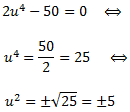
Las raíces son
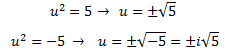
Por tanto, la factorización del polinomio es
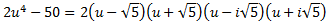
Es decir,
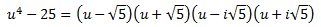
Podemos escribir el cociente como
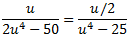
Aplicamos el Teorema Fundamental del Álgebra para descomponer la fracción
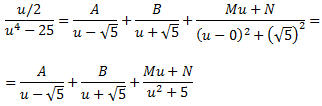
Sumamos las fracciones:
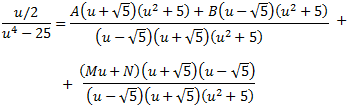
Damos valores a u en la siguiente igualdad para calcular las constantes A, B, M y N:
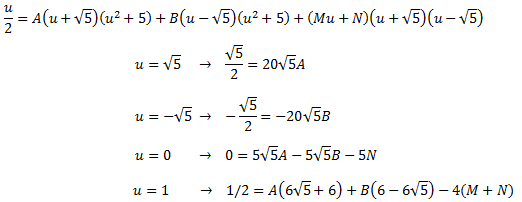
La solución el sistema de ecuaciones lineales es
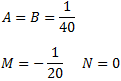
Con lo que la descomposición de la fracción es
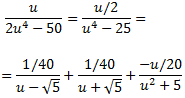
Reemplazamos la fracción del integrando por la suma de fracciones anterior para
descomponer la integral en una suma de integrales:
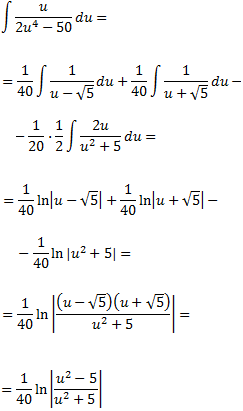
Finalmente deshacemos el cambio de variable
$$ e^x = u \leftarrow x = ln(u) $$
Por tanto, el resultado de la integral es
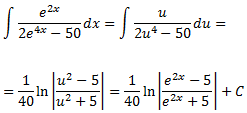
Integral 23
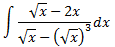
Solución
Aplicamos el cambio de variable
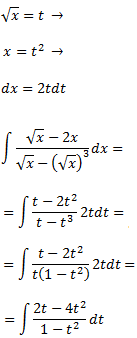
Dividimos los polinomios:
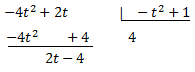
Por tanto, el dividendo es
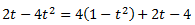
Dividiendo en la igualdad, obtenemos
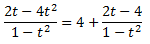
Con lo que podemos descomponer la integral
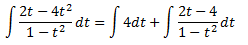
La primera integral es inmediata. Calculamos la segunda:
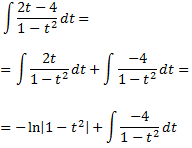
Resolvemos la última integral aplicando el Teorema Fundamental del Álgebra:
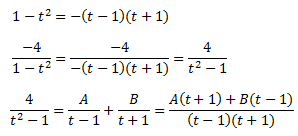
Para calcular las constantes, damos valores a t en la igualdad
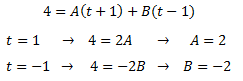
Luego la descomposición es
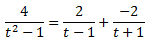
De donde
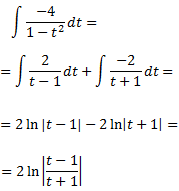
Con todo, tenemos
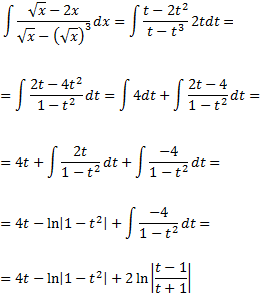
Finalmente, deshacemos el cambio de variable
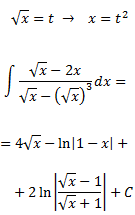
Integral 24
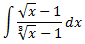
Solución
Aplicamos un cambio de variable. Nótese que si escogemos el cambio
$$ x = y^2 $$
Entonces,
$$ y = \sqrt{x} $$
Con lo que desaparece la raíz cuadrada. Pero
$$ \sqrt[3]{x} = \sqrt[3]{y^2} $$
Algo parecido ocurre si escogemos
$$ x = y^3 $$
Sin embargo, si escogemos como exponente al m.c.m(2,3) = 6 (mínimo común múltiplo), entonces
desaparecen ambos signos radicales:
$$ x = y^6 $$
Entonces,
$$ \sqrt{x} = \sqrt{y^6} = y^3 $$
$$ \sqrt[3]{x} = \sqrt[3]{y^2} = y^2$$
$$dx = 6y^5 dy $$
Aplicamos el cambio en la integral:
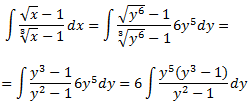
Dividimos los polinomios:
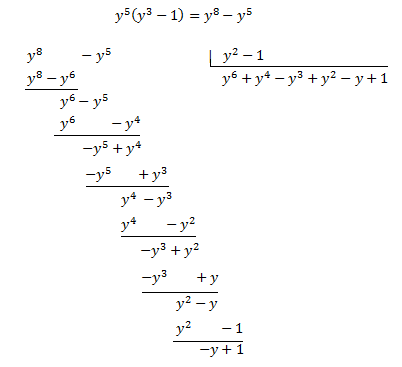
Por tanto, el numerador se puede escribir como
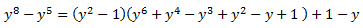
De donde obtenemos la siguiente descomposición:
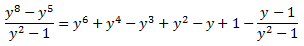
Con lo que podemos escribir la integral como suma de otras integrales:
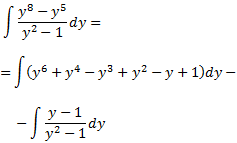
Nótese que la última integral es inmediata:
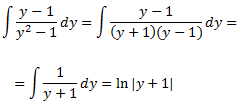
De este modo, el resultado de la integral es:
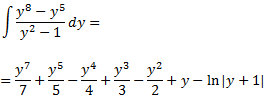
Tenemos que la integral inicial es
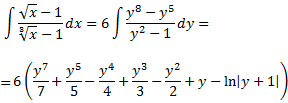
Deshacemos el cambio de variable
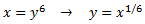
Y, sustituyendo, tenemos el resultado de la integral inicial:
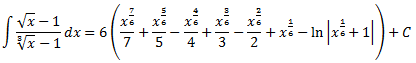
Nota: el resultado puede simplificarse más (las fracciones de las potencias no son irreducibles).
Integral 25 (dificultad alta)
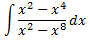
Solución
Buscamos las raíces del denominador. Pero antes, simplificamos la fracción:
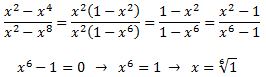
Recordamos que las raíces n-ésimas de un complejo z = a + bi son
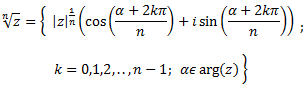
Y si a≠0, en el conjunto anterior podemos usar
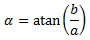
Tenemos que calcular las raíces 6-ésimas de z = 1:
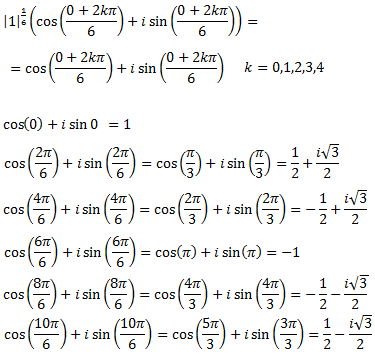
Por tanto, tenemos las 6 raíces
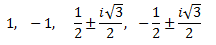
Aplicando el Teorema Fundamental del Álgebra, podemos escribir
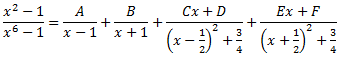
Damos valores a x en la siguiente igualdad para obtener las constantes:
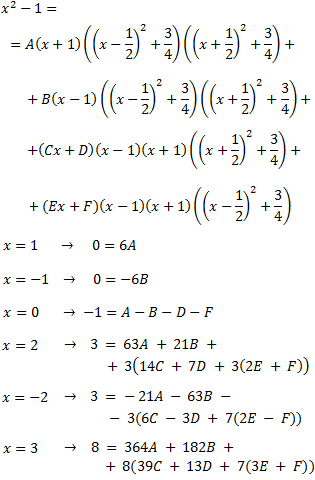
La solución del sistema de ecuaciones anterior es:
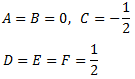
Luego la descomposición es
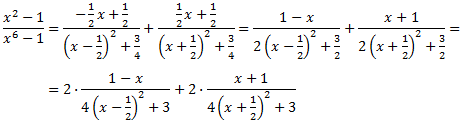
Por tanto, la integral inicial queda como
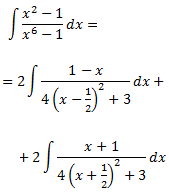
Resolvemos la primera integral:
Operamos en el integrando para obtener las derivadas del arctan y del ln
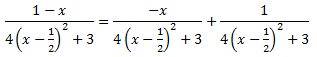
Operamos en la fracción anterior de la derecha:
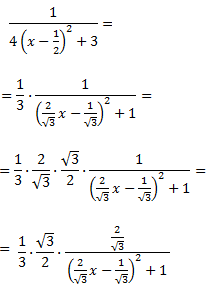
Por tanto,
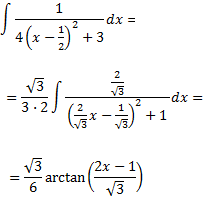
Calculamos la integral de la primera fracción, teniendo en cuenta que
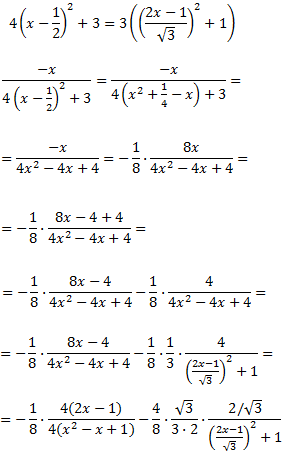
Por tanto,
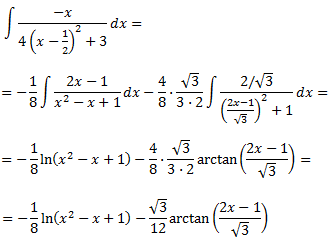
Ya tenemos la primera integral
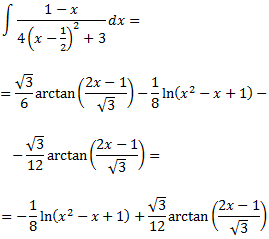
Si nos fijamos, sólo cambia el coeficiente director del polinomio del numerador. Obviamos el procedimiento ya que se obtiene de forma similar que la anterior:
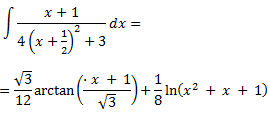
Finalmente, tenemos que