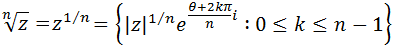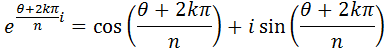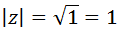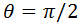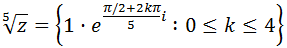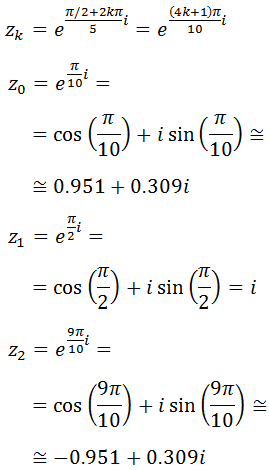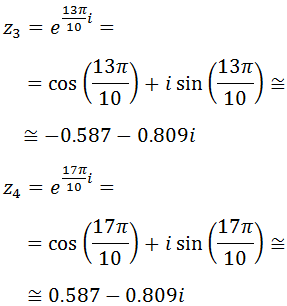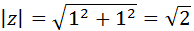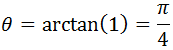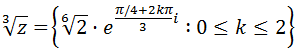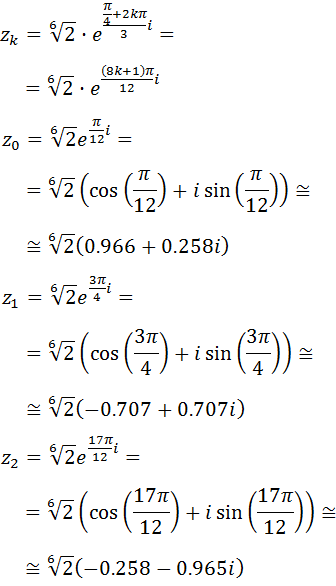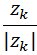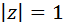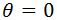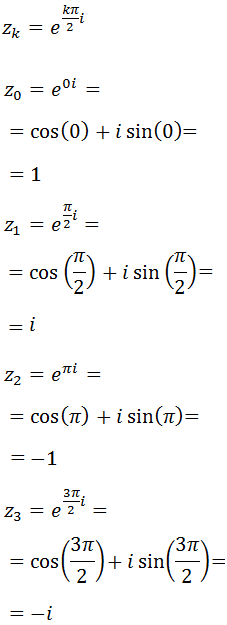Sean \(n\) un número natural y \(z\) un complejo, siendo \(|z|\) y \(\theta\) el módulo y el argumento de \(z\), respectivamente. Las raíces \(n\)-ésimas de \(z\) (o raíces de orden \(n\)) son
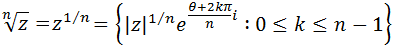
Observad que hay \(n\) raíces y, si las elevamos a \(n\), tenemos \(z\):
$$ (\sqrt[n]{|z|}·e^{\frac{\theta +2k\pi}{n}i})^n = $$
$$ = |z|·e^{\theta +2k\pi} = z $$
Para pasar a la forma binómica, aplicamos la fórmula de Euler:
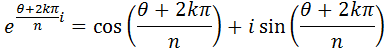
Nota: no hemos escrito el módulo para simplificar la identidad.
Las \(n\) raíces de \(z\) constituyen los vértices de un polígono regular de \(n\) lados centrado en el origen del plano complejo.
A continuación, calculamos las raíces quintas, cúbicas y cuartas de un complejo puro, de un complejo y de un complejo real, respectivamente.
Ejemplo 1
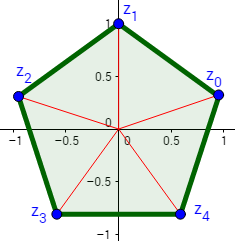
Raíces quintas de \(z = i\)
Ver operaciones
Calculamos las raíces quintas del complejo \(z = i\):
El módulo de \(z\) es
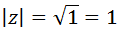
El argumento de \(z\) es
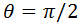
Las raíces quintas de \(z\) son
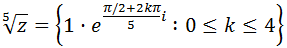
Calculamos las raíces:
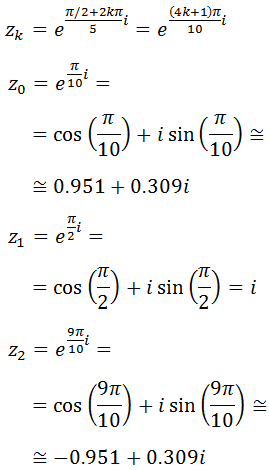
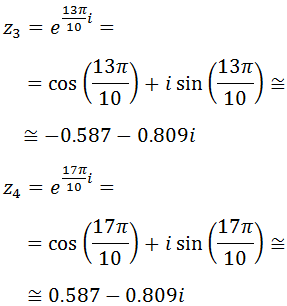
La representación de las raíces es un pentágono regular.
Ejemplo 2
Raíces cúbicas de \(z = 1+i\)
Ver operaciones
Calculamos las raíces 3-esimas del complejo \(z = 1+i\):
El módulo de \(z\) es
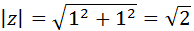
El argumento de \(z\) es
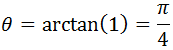
Las raíces cúbicas de \(z\) son
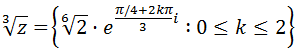
Calculamos las tres raíces cúbicas:
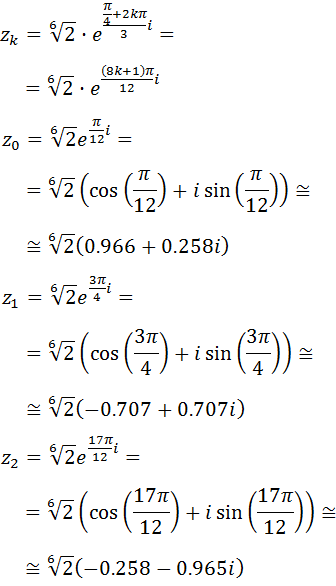
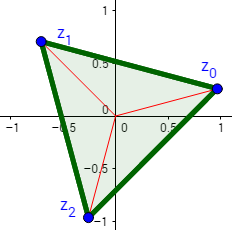
La representación de las raíces es un triángulo regular.
Nota: en realidad, en la figura hemos representado los complejos
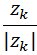
Así, sólo difiere el tamaño del polígono (la longitud de los segmentos rojos).
Ejemplo 3
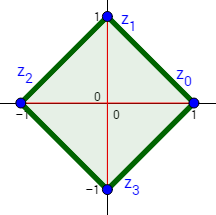
Raíces cuartas de \(z = 1\)
Ver operaciones
Calculamos las raíces cuartas del complejo real \(z = 1\):
El módulo de \(z\) es
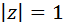
El argumento de \(z\) es
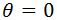
Las raíces quintas son

Calculamos las raíces:
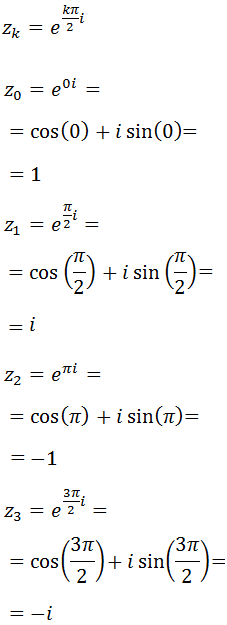
La representación de las raíces es un cuadrado.


Raíces enésimas de números complejos -
© matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.