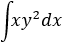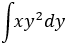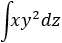Integrales inmediatas o directas resueltas
En esta página recordamos el concepto de primitiva y las propiedades de las integrales (de la suma/resta y de una constante) y resolvemos, muy detalladamente, 27 integrales directas o inmediatas.
Contenido de esta página:
- Introducción
- Recordatorio: concepto de integral y propiedades
- 27 integrales inmediatas resueltas
Páginas relacionadas:
Introducción
Este es el nivel básico del cálculo de primitivas después de las integrales que se obtienen directamente a partir de la tabla de derivadas.
Las llamamos inmediatas o directas ya que el método que usaremos consiste en, teniendo en cuenta las derivadas elementales (las de la tabla), conseguir en el integrando una función multiplicada por su derivada. Así, la primitiva es dicha función.
$$ \int{f(x)\cdot f'(x) }dx = f(x) + C $$
Necesitamos conocer:
- las derivadas elementales (la tabla de derivadas),
- las reglas de derivación (derivada de la suma, del cociente...) y la regla de la cadena ("derivada por la derivada de lo de dentro por la derivada de lo de dentro por..."
- y las propiedades básicas de las integrales.
No obstante, a continuación haremos un pequeño recordatorio de lo que necesitaremos.
Recordatorio
Definición de primitiva
Las primitivas de una función \(F(x)\) se representan por
$$ \int{F(x)}dx $$
Es el conjunto de funciones \(f(x)\) cuyas derivadas son iguales a \(F(x)\). Es decir, \(f(x)\) es una primitiva de \(F(x)\) si \( f'(x) = F(x)\).
Hablamos en plural ya que, por ejemplo, \( f(x) = x^2 + 1\) y \(g(x) = x^2 +2\) son dos primitivas distintas de \(F(x) = 2x\).
Observad que la diferencia entre ambas primitivas del ejemplo es la constante. Por ello, cuando resolvemos una integral, siempre escribimos la constante de integración, que puede tomar cualquier valor real y normalmente suele denotarse por \(K\) ó \(C\), aunque podemos usar otra letra:
$$ \int{f'(x)}dx = f(x) + C,\ C\in\mathbb{R}$$
Es suficiente con escribir la constante de integración al final y, sobre todo, debemos evitar a toda costa escribir constantes de integración complicadas, como suma de constantes distintas.
Ejemplo:
Si sumamos dos integrales, no debemos escribir la suma de sus dos respectivas constantes. Sean
$$ A = \int{f'(x)}dx = f(x) +K_1$$
$$ B = \int{g'(x)}dx = g(x) +K_2$$
Entonces, la suma de las integrales \(A\) y \(B\) es
$$ A+B = f(x) + g(x) + K$$
Escribimos la constante \(K\) y no la suma \(K_1 + K_2\).
Notación
En la expresión \(\int{f(x)}dx\),
- el símbolo \(\int{}\) es el signo integral (se debe a Leibniz y su origen es la letra \(S\), la inicial de "suma"),
- \(f(x)\) es el integrando,
- \(dx\) nos indica que la variable de integración es \(x\) y es habitual llamarla "diferencial de \(x\)" (cosa que no aconsejamos).
Ejemplos:
$$ \int{2yx}dx = yx^2+K$$
$$ \int{2yx}dy = y^2x+K$$
En la primera integral, tratamos la \(y\) como una constante, integrando respecto de \(x\). En la segunda, al contrario.
Propiedades de las integrales
La integral de la suma es la suma de las integrales:
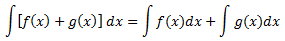
Es decir, la integral de la suma de dos funciones es la suma de las integrales de ambas funciones.
La integral de una constante por una función es la constante por la integral de la función:
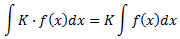
Es decir, las constantes (números o parámetros; o factores que no sean función de la variable de integración) salen fuera de la integral multiplicándola (o dividiéndola).
Esta propiedad será útil tanto de izquierda a derecha como de derecha a izquierda, pues en ocasiones necesitamos en el integrando un número para tener una derivada de una función, por lo que multiplicaremos y dividiremos la integral por este número y, aplicando la propiedad, podemos introducir el factor que multiplica (o el que divide) en el integrando.
Ejemplo:
$$ \int{x}dx = \frac{2}{2}\cdot \int{x}dx = $$
$$ = \frac{1}{2} \int{2x}dy = \frac{1}{2}\cdot x^2 + K $$
Hemos escrito el 2 en el integrando para tener \(2x\), que es la derivada de \(x^2\), por lo que la integral inicial es \(x^2/2 + K\).
Regla de la cadena:
Si \(f\) y \(g\) son dos funciones, entonces
$$ (f(g(x)))' = f'(g(x))\cdot g'(x) $$
De ahí lo de "la derivada por la derivada de lo de dentro por la derivada de lo dentro por..."
Integrales directas resueltas
Como estamos en el nivel más básico de integrales, intentaremos explicar cada integral lo más detalladamente posible.
Recordad que podemos comprobar el resultado derivando: si la derivada del resultado es el integrando, el resultado es correcto.
Integral 1 
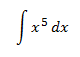
Aplicaremos la propiedad "una constante puede entrar o salir de la integral (multiplicando o dividiendo)".
La derivada de \(x^6\) es \(6x^5\), así que si tuviésemos ese 6 en la integral, la primitiva sería \(x^6\). Para ello, multiplicamos y dividimos por 6 en la integral e introducimos en la integral el 6 que multiplica:
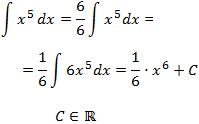
Integral 2 
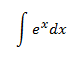
No tenemos que realizar ninguna operación para resolver esta integral porque \(e^x\) es la derivada de \(e^x\). Sólo debemos acordarnos de escribir la constante de integración \(C\):
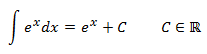
Integral 3 
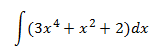
Aplicamos la propiedad de que la integral de la suma es la suma de las integrales:
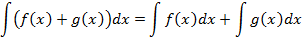
Así, podemos descomponer la integral como una suma de integrales más sencillas:
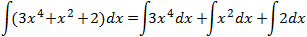
Primera integral:
El integrando \(3x^4\) se parece a la derivada de \(x^5\), que es \(5x^4\). Pero tenemos un 3 en lugar de un 5. Lo que haremos es, primero, sacar el 3 de la integral y, después, introducir un 5 en la integral (para esto último debemos multiplicar y dividir por 5):
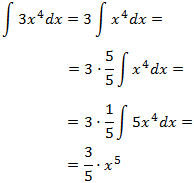
Segunda integral:
Sólo necesitamos un 3 en el integrando para tener la derivada de \(x^3\):
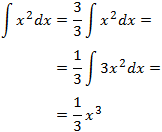
Tercera integral:
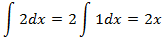
Por tanto, ya sólo falta sumar las tres integrales y, por supuesto, añadir la constante de integración:
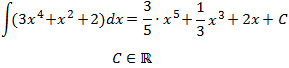
Integral 4 
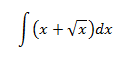
Empezamos escribiendo la integral como una suma de integrales:
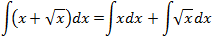
Primera integral:
Esta integral es muy fácil, sólo debemos añadir un 2 en el integrando para tener la derivada de \(x^2\):
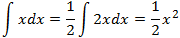
Segunda integral:
Como tenemos una raíz cuadrada, la escribimos como un potencia de exponente 1/2:
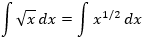
Al escribir la raíz como un exponente, podemos resolver la integral como hemos ido haciendo con las potencias: el coeficiente de la \(x\) tiene que ser mayor que su exponente en una unidad. Lo veremos más claro si calculamos la derivada de la potencia \(x^{1/2 + 1}\):
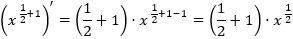
Es decir, obtenemos nuestro integrando pero multiplicado por el número \(\frac{1}{2}+1\) (el exponente más 1). Luego solo tenemos que multiplicar y dividir por dicho número en la integral:
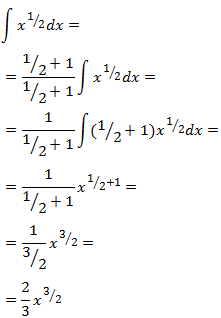
Finalmente, sumamos las integrales y añadimos la constante de integración:
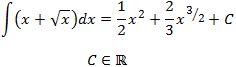
Integral 5 
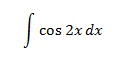
La derivada de \(sin(x)\) es \(cos(x)\), así que, aplicando la regla de la cadena, la derivada de \(sin(2x)\) es \(cos(2x)\cdot 2\). Por tanto, si escribimos un 2 en el integrando, tendremos la derivada del seno del ángulo doble:
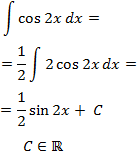
Nota: como \(\sin(2x) = 2\sin(x)\cdot\cos(x)\), el resultado de la integral también puede ser \(\sin(x)\cdot\cos(x) + C\).
Integral 6 
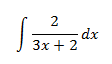
Normalmente, las integrales inmediatas de funciones racionales son la derivada de un logaritmo. Si no es así, tendremos que aplicar otros métodos para integrales de funciones racionales.
Recordad la derivada del logaritmo:
$$ (\ln|f(x)|)' = \frac{1}{f(x)} \cdot f'(x) $$
El integrando será la derivada de un logaritmo si conseguimos escribir el numerador como la derivada del denominador.
Como la derivada del denominador es 3, deberíamos tener un 3 en lugar de un 2 en el numerador. Sin embargo, este problema es fácil de resolver porque podemos extraer el 3 e introducir un 2:
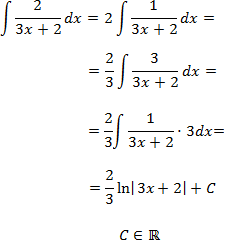
Nota: no hay que olvidar el valor absoluto del argumento del logaritmo porque éste no puede tomar valores no positivos.
Integral 7 
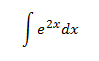
Introducimos un 2 en el integrando para que éste sea la derivada de \(e^{2x}\):
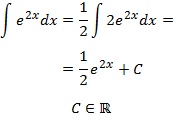
Integral 8 
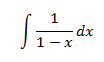
Como es una función racional simple, su integral será un logaritmo:
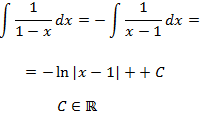
Integral 9 
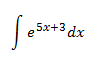
Introducimos un 5 en el integrando para convertirlo en la derivada de \(e^{5x+3}\):
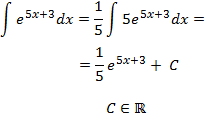
Integral 10 
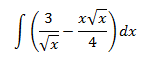
Lo primero que haremos es descomponer la integral en dos integrales:
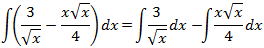
Como tenemos raíces, las escribiremos como potencias (recordad la Integral 4).
Primera integral:
Que la raíz cuadrada esté en el denominador no nos importa demasiado porque podemos escribir el exponente negativo:
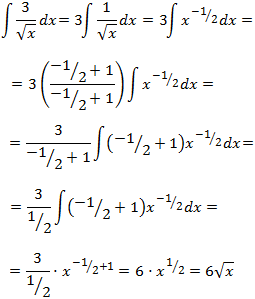
Segunda integral:
Seguimos de nuevo el mismo procedimiento, aunque primero escribiremos el producto de las potencias como una única potencia (sumando los exponentes):
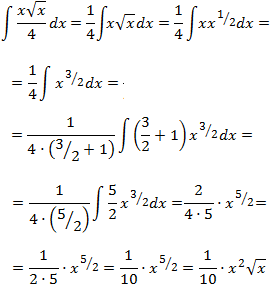
Finalmente, sumamos y añadimos la constante de integración:
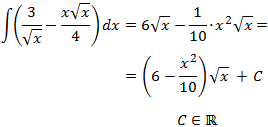
Integral 11 
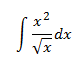
Vamos a escribir la raíz cuadrada en forma de potencia para poder aplicar las propiedades de las potencias (cociente de potencias).
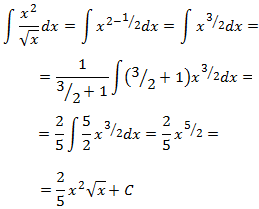
Integral 12 
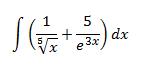
Primero, escribimos la integral como la suma de dos integrales:
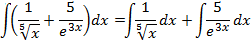
Primera integral:
Escribimos la raíz como una potencia con exponente \(-1/5\):
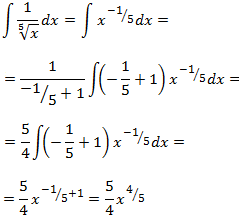
Hemos multiplicado y dividido por \(-1/5+1\) para tener la derivada de \(x^{4/5}\) en el integrando.
Segunda integral:
Aunque tengamos la exponencial en el denominador, no tenemos (ni podemos tener) la derivada del mismo en el numerado. Esto significa que el integrando no es la derivada de un logaritmo. Sólo tenemos que, al igual que antes, escribir la exponencial con exponente negativo:
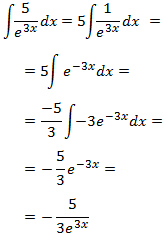
Finalmente, sumamos y añadimos la constante de integración:
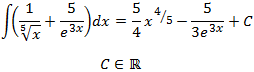
Integral 13 
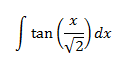
Normalmente, escribir la tangente como el cociente del seno y del coseno facilita los cálculos. Al hacerlo, tendremos un cociente de funciones trigonométricas siendo el numerador la derivada del denominador.
Escribimos la tangente como un cociente:
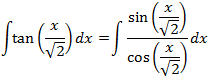
Recordad la derivada del logaritmo:
$$ (\ln|f(x)|)' = \frac{1}{f(x)} \cdot f'(x) $$
Nuestro integrando es una fracción:
- en el denominador tenemos un coseno y
- en el numerador, un seno, que es la derivada del coseno (sin tener en cuenta el signo y la derivada del argumento).
En el numerador hacen falta un signo negativo y la derivada del argumento, que es \(1/\sqrt{2}\), para tener la derivada del denominador. Por tanto,
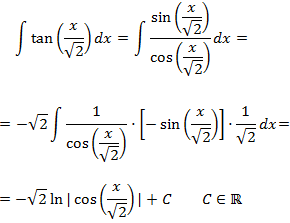
Integral 14 
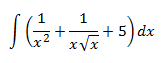
Ya hemos resuelto integrales parecidas a esta: escribimos la integral como una suma de integrales y aprovechamos las propiedades de las potencias para simplificar los integrandos.
Escribimos la integral como una suma:
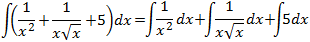
Resolvemos la primera integral (aunque en realidad es directa):
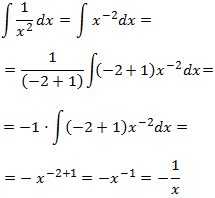
Resolvemos la segunda integral (aplicando propiedades de las potencias):
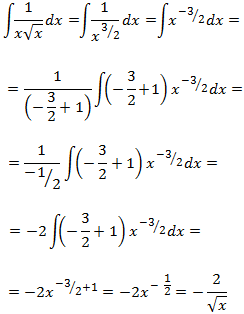
La integral de 5 es obviamente \(5x\).
Sumamos y añadirmos la constante de integración:
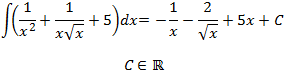
Nota: la integral de \(1/(x^2)\) es tan habitual que se suele escribir directamente su primitiva (debemos saberla).
Problema adicional para pensar 
Con todo lo visto anteriormente, deberíamos saber resolver las siguientes integrales:
Lo que cambia en las integrales es la variable de integración.
Primera integral:
Como la variable de integración es \(x\), debemos considerar \(y^2\) como una constante:
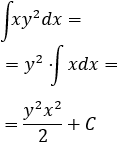
Segunda integral:
En esta integral, la constante es \(x\):
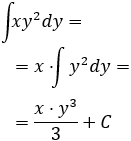
Tercera integral:
Como la variable de integración es \(z\), tanto \(x\) como \(y^2\) son constantes:
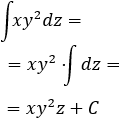
siendo \(C\in\mathbb{R}\).
Integral 15 
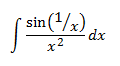
Si escribimos la fracción como un producto de fracciones, se observa mejor que tenemos un seno multiplicado casi por la derivada de su argumento (faltaría un signo negativo). Por tanto, se trata de la derivada del coseno:
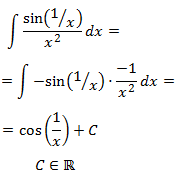
Integral 16 
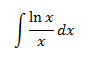
El integrando es la derivada del cuadrado del logaritmo (dividido entre 2):
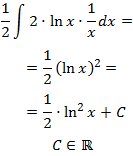
Integral 17 
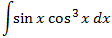
Es una integral casi directa.
Nos fijamos en el factor que tiene exponente mayor: \(\cos^3(x)\). Observad que la derivada de \(\cos^4(x)\) es \(4\cos^3(x)·(-\sin(x)\), que es casi el integrando que tenemos (falta el 4 y el signo negativo).
Por tanto,
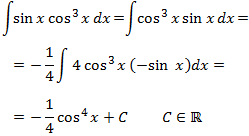
Integral 18 
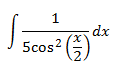
Record la derivada de la tangente:
$$ (\tan(f(x)))' = \frac{1}{\cos^2(f(x))}\cdot f'(x) $$
El integrando es casi la derivada de la tangente del ángulo medio:
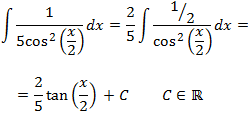
Integral 19 

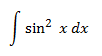
Esta integral es muy importante en cuanto a que aparece con frecuencia y para poder resolverla debemos recordar la siguiente identidad trigonométrica:
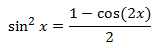
Sustituimos en la integral y la escribimos como una suma:
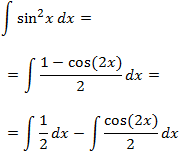
La primera integral es fácil: es \(x/2\). Calculamos la segunda:
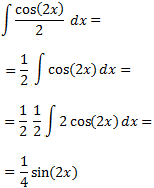
Finalmente, sumamos y añadimos la constante de integración:
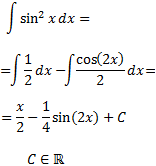
Nota: como \(\sin(2x) = 2\sin(x)\cdot\cos(x)\), el resultado de la integral también puede ser
$$ \frac{1}{2}\cdot(x - \sin(x)\cdot \cos(x)) + C$$
Integral 20 

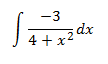
El integrando es una fracción, pero la primitiva no puede ser un logaritmo porque no tenemos (ni podemos tener) la derivada del denominador en el numerador (en el denominador tenemos grado 2 y en el numerador grado 0).
Solamente debemos recordar la derivada del arcotangente:
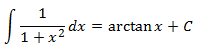
Podemos operar en el integrando para obtener la derivada de un arcotangente. Para que sea más fácil de entender el desarrollo, adelantamos que vamos a transformar el integrando en la derivada del \(\arctan\left( \frac{x}{2}\right)\), es decir,
$$ \left( \arctan\left( \frac{x}{2}\right) \right)' = \frac{1/2}{1 + (x/2)^2} $$
Operamos:
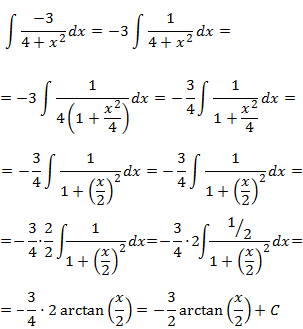
Este tipo de integrales suelen aparecer con frecuencia, por lo que podemos bien recordar el desarrollo seguido para repetirlo (lo aconsejamos) o bien generalizarlo para obtener una fórmula (que deberíamos memorizar):

Integral 21 
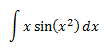
El seno es la derivada del coseno (si tuviera un signo negativo) y está multiplicado casi por la derivada del argumento (le falta el 2). Luego tenemos que añadir un 2 negativo:
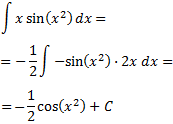
Integral 22 
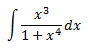
Tenemos un cociente de polinomios y el grado del numerador es un grado menor que el del denominador, así que podría ser posible escribir el numerador como la derivada del denominador. En tal caso, tendríamos la derivada del logaritmo del denominador:
$$ (\ln|f(x)|)' = \frac{1}{f(x)} \cdot f'(x) $$
Sólo necesitamos un 4 en el numerador:
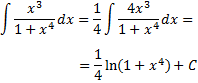
Nota: no es necesario escribir el valor absoluto en el logaritmo ya que su argumento es siempre positivo.
Integral 23 
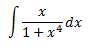
De nuevo tenemos un cociente de polinomios, pero el numerador no es (ni puede ser) la derivada del denominador porque el grado del polinomio del numerador es 1 y el del denominador es 4.
Recordad la derivada del \(\arctan\):
$$ (\arctan( f(x) )' = \frac{1}{1 + f^2(x)}\cdot f'(x) $$
Podemos escribir el denominador como \(1 + (x^2)^2\) para que tenga la forma de la derivada del \(\arctan(x^2)\). Entonces, en el numerador tendría que haber \(2x\) para que sea la derivada del argumento del \(\arctan\):
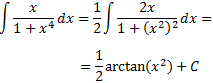
Integral 24 
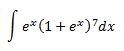
Observemos:
- La derivada de \(e^x\) es \(e^x\);
- La derivada de \(1+e^x\) es \(e^x\);
- Por la regla de la cadena, la derivada de \((1+e^x)^8\) es \(8\cdot (1+e^x)^7 \cdot e^x\)
Por tanto, sólo hace falta un 8 en el integrando para tener la derivada de \((1+e^x)^8\):
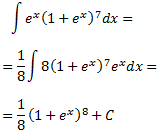
Integral 25 
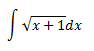
Como de costumbre, escribimos la raíz como una potencia:
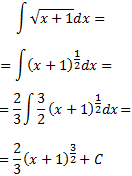
Integral 26 
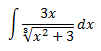
Primero, escribimos la raíz como una potencia. Como se halla en el denominador, podemos usar exponente negativo para que esté en el numerador:
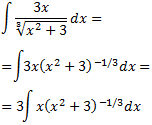
En el integrando tenemos la potencia \((x^2+3)^{1/3}\) multiplicada casi por la derivada de su base (le falta un 2). Si escribimos el 2 y \(-1/3+1 = 2/3\) en el integrando, tendremos la derivada de \((x^2+3)^{2/3}\):
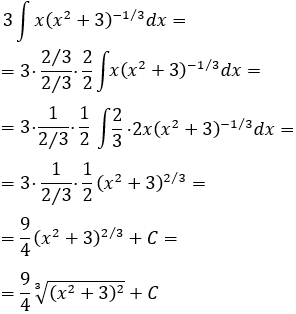
Por tanto,
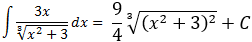
Integral 27 
$$ \int{\frac{x-1}{\sqrt{2x}+\sqrt{x+1}}} $$
Sólo tenemos que operar un poco para simplificar el integrando.
Como tenemos una suma de raíces en el denominador, podemos multiplicar y dividir la fracción por la diferencia de las mismas raíces. Esto nos permite aplicar el producto notable "suma por diferencia es igual a diferencia de cuadrados", con lo que desaparecen los signos radicales. Finalmente, habremos logrado un polinomio en el denominador y una resta de raíces en el numerador.
Vamos, pues, a multiplicar y dividir por la resta de raíces
$$\sqrt{2x}-\sqrt{x+1}$$
Operamos:
$$ \frac{x-1}{\sqrt{2x}+\sqrt{x+1}} \cdot \frac{\sqrt{2x}-\sqrt{x+1}}{\sqrt{2x}-\sqrt{x+1}} =$$
$$ =\frac{(x-1)\cdot (\sqrt{2x}-\sqrt{x+1}) }{(\sqrt{2x})^2-(\sqrt{x+1})^2} =$$
$$ =\frac{(x-1)\cdot (\sqrt{2x}-\sqrt{x+1}) }{2x-(x+1)} =$$
$$ =\frac{(x-1) \sqrt{2x}-(x-1)\sqrt{x+1} }{2x-x-1} =$$
$$ =\frac{(x-1) \sqrt{2x}-(x-1)\sqrt{x+1} }{x-1} =$$
$$ =\frac{\sqrt{2x}-\sqrt{x+1} }{1} =$$
$$ =\sqrt{2x}-\sqrt{x+1}$$
La integral de la resta anterior es sencilla:
$$ \int{(\sqrt{2x}-\sqrt{x+1})dx}=$$
$$ =\int{\sqrt{2x}dx}-\int{\sqrt{x+1}dx}=$$
$$ =\frac{(2x)^\frac{3}{2}}{3}-\frac{2(x+1)^\frac{3}{2}}{3}+C$$

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.