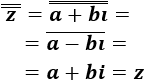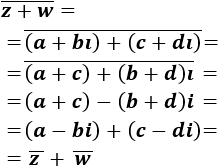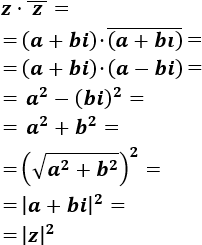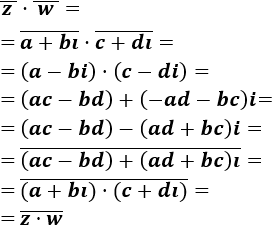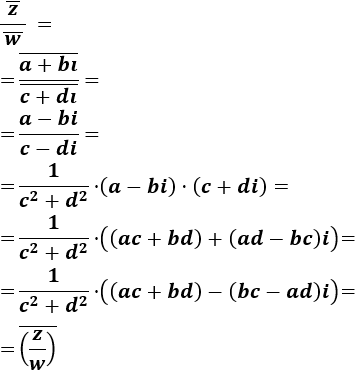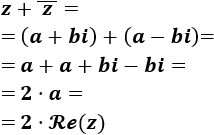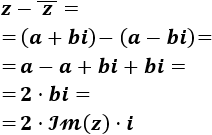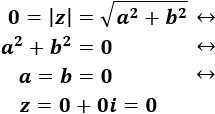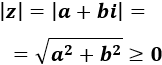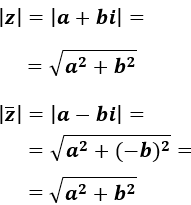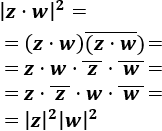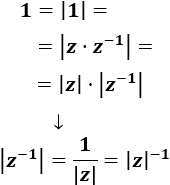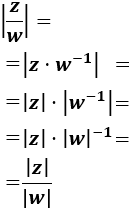Problema 1
Todo complejo es igual al conjugado de su conjugado:
$$ \overline{\overline{z}} = z $$
Ver solución
Sea el complejo \(z = a +bi\). El conjugado se calcula cambiando el signo a la parte imaginaria:
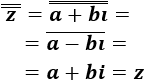
Problema 2
El conjugado de una suma de complejos es la suma de sus conjugados:
$$ \overline{z+w} = \overline{z}+\overline{w}$$
Ver solución
Sean los complejos
$$ z = a + bi $$
$$ w = c + di $$
Calculamos el conjugado de la suma:
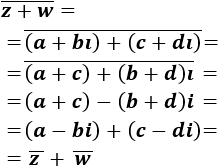
Problema 3
El producto de un complejo por su conjugado es el cuadrado de su módulo:
$$ z·\overline{z} = |z|^2$$
Ver solución
Sea \(z = a+bi\), su conjugado es \(\overline{z} = a-bi\).
Calculamos el producto:
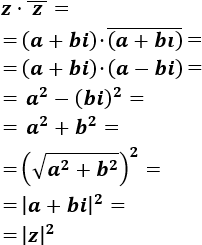
Problema 4
El conjugado de un producto de complejos es el producto de sus conjugados:
$$ \overline{z·w} = \overline{z}·\overline{w} $$
Ver solución
Sean los complejos
$$ z = a + bi $$
$$ w = c + di $$
Calculamos el producto de los conjugados::
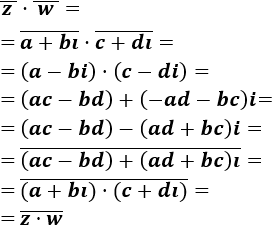
Problema 5
El conjugado de un cociente de complejos es el cociente de sus conjugados:
$$ \overline{\left( \frac{v}{w}\right)} = \frac{\overline{z}}{\overline{w}}$$
Ver solución
Sean los complejos
$$ z = a + bi $$
$$ w = c + di $$
Calculamos el cociente de los conjugados:
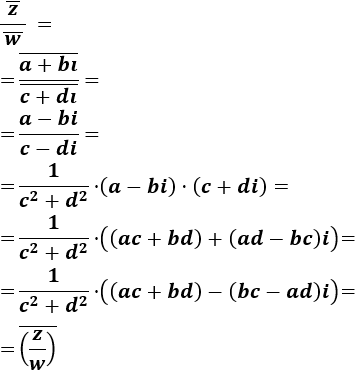
Problema 6
La suma de un complejo \(z\) y de su conjugado es el doble de la parte real de \(z\):
$$ z + \overline{z} = 2·\mathcal{Re}(z) $$
Ver solución
Sea el complejo
$$ z = a + bi $$
La suma de \(z\) con su conjugado es
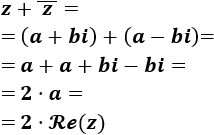
Problema 7
La resta de un complejo \(z\) y de su conjugado es el doble de la parte imaginaria de \(z\) por la unidad imaginaria \(i\):
$$ z - \overline{z} = 2·\mathcal{Im}(z) ·i$$
Ver solución
Sea el complejo
$$ z = a + bi $$
La resta de \(z\) con su conjugado es
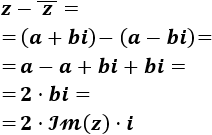
Problema 8
El módulo de un complejo es nulo si, y sólo si, es el complejo nulo:
$$ |z| = 0 \leftrightarrow z = 0$$
Ver solución
Sea el complejo
$$ z = a + bi $$
Entonces,
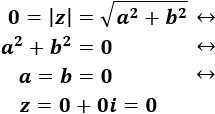
Problema 9
El módulo de un complejo es simpre no negativo:
$$ |z| ≥ 0 $$
Ver solución
Sea el complejo
$$ z = a + bi $$
Su módulo es no negativo por ser la raíz cuadrada de la suma de dos números no negativos:
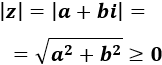
Problema 10
El módulo de un complejo es igual al módulo de su conjugado:
$$ |z| = |\overline{z}| $$
Ver solución
Sea el complejo
$$ z = a + bi $$
El módulo de \(z\) y el de su conjugado son
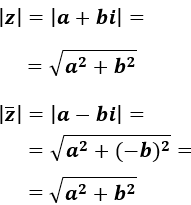
Problema 11
El módulo de un complejo \(z\) es mayor o igual que el valor absoluto de su parte real y de su parte imaginaria:
$$ |\mathcal{Re}(z)|\leq |z| $$
$$ |\mathcal{Im}(z)|\leq |z| $$
Ver solución
Sea el complejo
$$ z = a+bi $$
Su parte real, su parte imaginaria y su módulo son
$$ \mathcal{Re}(z) = a $$
$$ \mathcal{Im}(z) = b $$
$$ |z| = \sqrt{a^2 +b^2}$$
Usaremos que la raíz cuadrada de un número al cuadrado es el valor absoluto del número, es decir,
$$ \sqrt{k^2} = |k| $$
Acotamos el valor absoluto de la parte real:
$$ |\mathcal{Re}(z)| = |a| = $$
$$ = \sqrt{a^2} \leq \sqrt{a^2 + b^2} = |z| $$
De forma análoga,
$$ |\mathcal{Im}(z)| = |b| = $$
$$ = \sqrt{b^2} \leq \sqrt{a^2 + b^2} = |z| $$
Problema 12
El módulo del producto de complejos es el producto de sus módulos:
$$ |z·w| = |z|·|w| $$
Ver solución
Sean los complejos
$$ z = a + bi $$
$$ w = c + di $$
Vamos a utilizar la propiedad del Problema 3 (\(z·\overline{z} = |z|^2\)) y la propiedad del Problema 4 (\(\overline{z·w} = \overline{z}·\overline{w}\)):
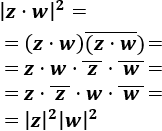
Tomando raíces cuadradas en la igualdad obtenida,
$$ |z·w| = |z|·|w| $$
Problema 13
El módulo del inverso de un complejo \(z\neq 0\) es el inverso del módulo de \(z\):
$$ |z^{-1}| = |z|^{-1}$$
Ver solución
Por definición del inverso,
$$ z\cdot z^{-1} = 1$$
Teniendo en cuenta que el módulo del producto de complejos es el producto de sus módulos,
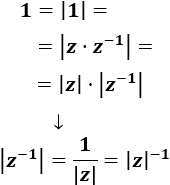
Problema 14
El módulo del cociente de dos complejos es el cociente de sus módulos:
$$ \left| \frac{z}{w} \right| = \frac{|z|}{|w|} $$
Ver solución
Usaremos la propiedad del módulo del producto:
$$ |z\cdot w| = |z|\cdot |w| $$
También, la propiedad del módulo del inverso:
$$ |z^{-1}|=|z|^{-1} $$
La demostración es inmediata:
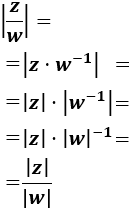
Problema 15
Valor absoluto de la parte imaginaria y de la parte real del producto de complejos:
$$ |\mathcal{Re}(z·w)| ≤ |w|·|z|$$
$$ |\mathcal{Im}(z·w)| ≤ |w|·|z|$$
Ver solución
La propiedad del Problema 11 es
$$ |\mathcal{Re}(z)|\leq |z| $$
$$ |\mathcal{Im}(z)|\leq |z| $$
Por tanto,
$$ |\mathcal{Re}(z·w)|\leq |z·w| $$
$$ |\mathcal{Im}(z·w)|\leq |z·w| $$
Como el módulo del producto es el producto de los módulos,
$$ |\mathcal{Re}(z·w)|\leq |z|·|w| $$
$$ |\mathcal{Im}(z·w)|\leq |z|·|w| $$
Problema 16
Versión compleja de la desigualdad triángular:
$$ |z+w| \leq |z| + |w| $$
Ver solución
Necesitaremos todas las siguientes propiedades demostradas anteriormente:
$$ \begin{align} & |Re(z)| \leq |z| \\
& |z\cdot w| = |z|\cdot |w| \\
& |z| = |\overline{z}|\\
& z\cdot \overline{z} = |z|^2 \\
& \overline{z+w} = \overline{z}+\overline{w} \\
& z + \overline{z} = 2\cdot Re(z) \\
& \overline{\overline{z}} = z \end{align} $$
Vamos a desarrollar el cuadrado del módulo de la suma de los
complejos v y w. Después, tomaremos raíces a ambos lados
de la desigualdad:



Demostraciones de las propiedades básicas de los números complejos-
© -
matesfacil.com

Matesfacil.com
by J. Llopis is licensed under a
Creative
Commons Attribution-NonCommercial 4.0 International License.