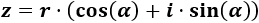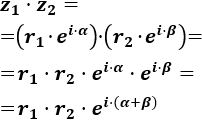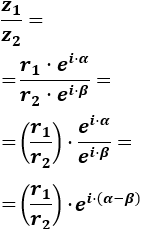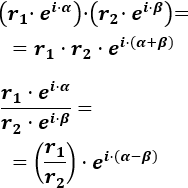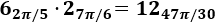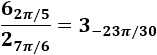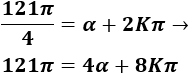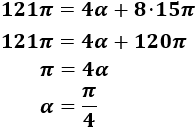logotipo matesfacil

Números complejos o imaginarios en forma polar

Contenido de esta página:

  1. Recordatorio de la forma binómica
  2. Forma polar de un complejo
  3. Calculadora online pasar de la forma binómica a la polar y viceversa (y ejemplos)
  4. Producto y cociente de complejos en forma polar
  5. Problemas resueltos

Enlaces:

1. Forma binómica de un complejo

Recordad que un complejo en (forma binómica) es \(z = a+b·i\), siendo \(a\) y \(b\) números reales. La parte real del complejo \(z\) es \(\mathcal{Re}(z) = a\) y la parte imaginaria es \(\mathcal{Im}(z) = b\).

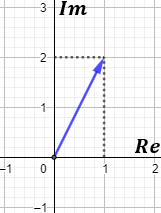
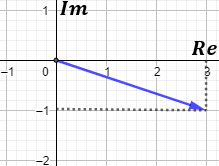
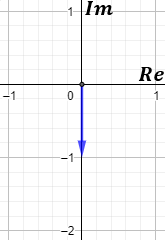
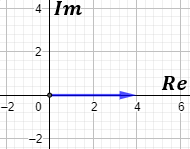
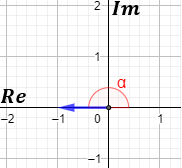
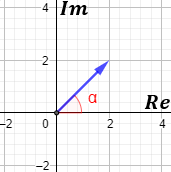
Los complejos se representan en el plano complejo, que es como el plano cartesiano. El complejo \(z = a+b·i\) se representa como el vector \((a,b)\) en el plano real:

Números complejos o imaginarios en forma polar. Calculadora online para pasar de la forma polar a la binómica y viceversa. Incluye las fórmulas para multiplicar y dividir complejos en forma polar. Con problemas resueltos y representaciones. Matemáticas para bachillerato y universidad. TIC

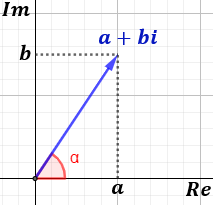
Es decir, la primera coordenada del vector es la parte real y la segunda coordenada es la parte imaginaria.

2. Forma polar de un complejo

Si vemos los complejos como vectores, es lógico pensar en su módulo \(r =|z|\) (longitud del vector) y en el ángulo \(\alpha\) que forma el vector con el eje real.

La forma trigonométrica de un complejo \(z\) con módulo \(r\) y ángulo \(\alpha\) es

Números complejos o imaginarios en forma polar. Calculadora online para pasar de la forma polar a la binómica y viceversa. Incluye las fórmulas para multiplicar y dividir complejos en forma polar. Con problemas resueltos y representaciones. Matemáticas para bachillerato y universidad. TIC

La forma polar de un complejo es cualquiera de las siguientes:

Números complejos o imaginarios en forma polar. Calculadora online para pasar de la forma polar a la binómica y viceversa. Incluye las fórmulas para multiplicar y dividir complejos en forma polar. Con problemas resueltos y representaciones. Matemáticas para bachillerato y universidad. TIC

Para pasar de la forma polar a la binómica, utilizamos la forma trigonométrica (calculando el seno y el coseno del ángulo).

Veamos ahora cómo se definen y calculan el módulo y el ángulo:

El módulo de un complejo \(z = a+b·i\) se representa por \(|z|\) y se define como

$$ |z| = \sqrt{a^2+b^2} \geq 0$$


El ángulo \(\alpha\) de \(z\) se calcula con la función inversa de la tangente:

$$ \alpha = atan\left( \frac{b}{a}\right)$$

Nota: cuando el complejo está sobre el eje vertical o es nulo, es decir, si \(a=0\), entonces el ángulo es

  • \(\alpha = \pi/2\) (90 grados) si \(b>0\),
  • \(\alpha = -\pi/2\) (-90 grados) si \(b< 0\) y
  • \(\alpha = 0\) si \(b=0\).

Además de esto, la función arcotangente proporciona ángulos entre \(-\pi/4\) y \(\pi/4\). Así que,

  • Si el complejo está en el segundo cuadrante (\(a<0\), \(b>0\)), hay que sumar \(\pi \) al ángulo obtenido.

  • Si el complejo está en el tercer cuadrante (\(a<0\), \(b<0\)), hay que restar \(\pi\) al ángulo obtenido.

Recordad que un vector con módulo \(|z|\) y ángulo \(\alpha\) es equivalente al vector con el mismo módulo y ángulo \(\alpha + 2k\pi\). Es por esta razón por la que se define el argumento principal:

El argumento principal de \(z\) se representa por \(Arg(z)\) y es el ángulo de \(z\) equivalente en el intervalo \(\left]-\pi, \pi \right]\).

3. Calculadoras para pasar de la forma binómica a la polar y viceversa

Las entradas de las calculadoras pueden ser fracciones utilizando una barra (como 2/4) o números decimales exactos utilizando un punto (como 2.123). Las calculadoras aproximan con 3 decimales.

Para pasar de la forma polar a la binómica sólo tenemos que calcular el seno y el coseno del ángulo y multiplicar por su módulo.

Ejemplo: el número complejo \(z = 2_{\pi /3} \) en forma binómica es \(z = 1+\sqrt{3}·i\).

Ver operaciones

Calculadora 1: De forma binómica a polar

\(z_1 = \)\(+\)\(·i\)

Para pasar de la forma binómica a la polar tenemos que calcular el módulo y el ángulo.

Ejemplo: el complejo \(z = 2\sqrt{3}+2i \) en forma polar es \(4_{\pi/6}\).

Ver operaciones

Calculadora 2: De forma polar (en grados) a binómica

Módulo:

Ángulo (en grados): \(\alpha = \) \(^\circ \)

4. Producto y cociente en forma polar

La forma polar nos permite calcular el producto y el cociente de dos complejos muy rápidamente por las propiedades de las potencias.

Consideremos los complejos \(z_1 = r_1·e^{i·\alpha}\) y \(z_2 = r_2·e^{i·\beta}\).

Calculamos su producto:

Números complejos o imaginarios en forma polar. Calculadora online para pasar de la forma polar a la binómica y viceversa. Incluye las fórmulas para multiplicar y dividir complejos en forma polar. Con problemas resueltos y representaciones. Matemáticas para bachillerato y universidad. TIC

Nota: si trabajamos con la forma polar que no utiliza la exponencial, no importa:

El producto de los complejos tiene módulo \(r=r_1·r_2\) y ángulo \(\alpha + \beta\).

Calculamos su cociente:

Números complejos o imaginarios en forma polar. Calculadora online para pasar de la forma polar a la binómica y viceversa. Incluye las fórmulas para multiplicar y dividir complejos en forma polar. Con problemas resueltos y representaciones. Matemáticas para bachillerato y universidad. TIC


El cociente de los complejos tiene módulo \(r=r_1·r_2\) y ángulo \(\alpha - \beta\).

5. Problemas resueltos

Problema 1

Representar los siguientes complejos dados en su forma polar o binómica:

  • \(z = 1+2i\)

  • \(z = 3-i\)

  • \( z = -i\)

  • \( z = 4_{0}\)

  • \( z = 1_{\pi}\)

  • \( z = 2\sqrt{2}_{\pi/4}\)

Ver solución

Problema 2

Calcular el módulo y el ángulo (en grados) de los complejos del problema anterior.

Ver solución

Problema 3

Escribir en forma binómica los siguientes complejos escritos en forma polar:

  1. \( z = 8_{30°}\)

  2. \( z = 2_{120°}\)

  3. \( z = \sqrt{2}_{135°}\)

Ver solución

Problema 4

Calcular el producto y el cociente de los siguientes pares de complejos escritos en su forma polar:

  1. \(z_1 = 1_{3\pi/4}\) y \(z_2 = 3_{2\pi/4}\)

  2. \(z_1 =6_{2\pi/5}\) y \(z_2 = 2_{7\pi/6}\)

Ver solución

Problema 5

Calcular el argumento principal de los siguientes complejos:

  1. \( z = 1_{121\pi/4}\)

  2. \( z = \sqrt{2}_{-97\pi/5}\)

Ver solución


contacto

ejercicios interactivos de matemáticas


Números complejos en forma polar - © - matesfacil.com

Creative Commons License
Matesfacil.com by J. Llopis is licensed under a Creative Commons Attribution-NonCommercial 4.0 International License.