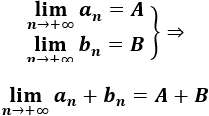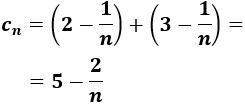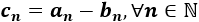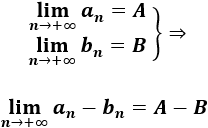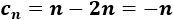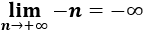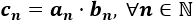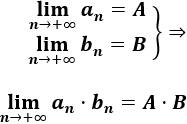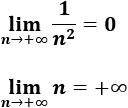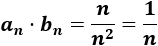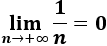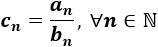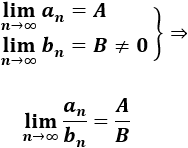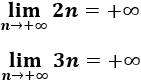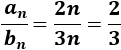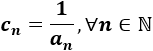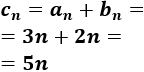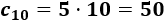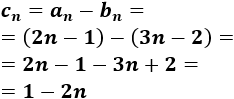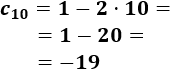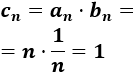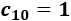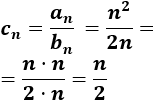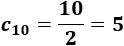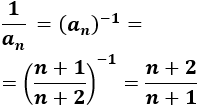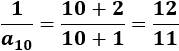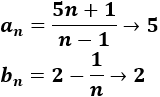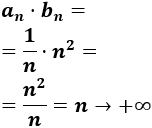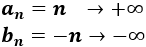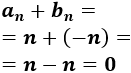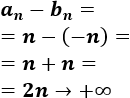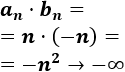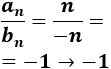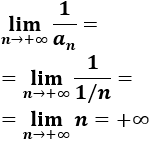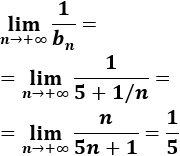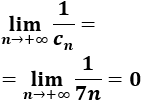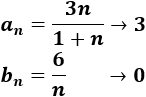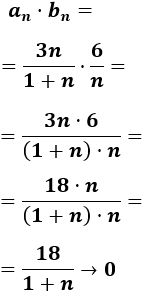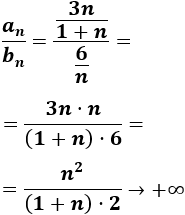Problema 1
Calcular el término general \(c_n\) de la suma de las sucesiones, completar la siguiente tabla y calcular el décimo término de la suma:
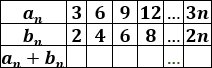
Ver solución
Calculamos el término general de la suma:
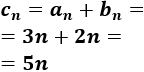
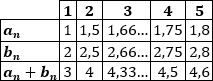
Completamos la tabla:
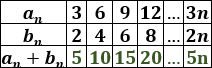
Calculamos el décimo término:
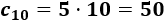
Problema 2
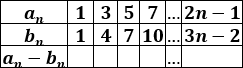
Calcular el término general \(c_n\) de la resta de las sucesiones, completar la siguiente tabla y calcular el décimo término de la resta:
Ver solución
Calculamos el término general de la resta:
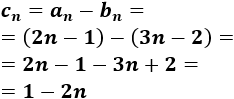
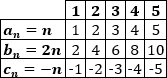
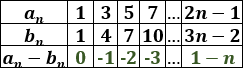
Completamos la tabla:
Calculamos el décimo término:
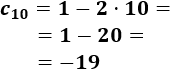
Problema 3
Calcular el término general \(c_n\) del producto de las sucesiones, completar la siguiente tabla y calcular el décimo término del producto:

Ver solución
Calculamos el término general del producto:
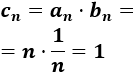
Completamos la tabla:
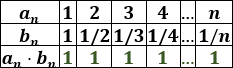
Calculamos el décimo término:
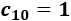
Problema 4
Calcular el término general \(c_n\) del cociente de las sucesiones, completar la siguiente tabla y calcular el décimo término del cociente:

Ver solución
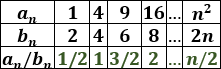
Calculamos el término general del cociente:
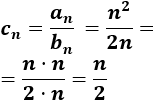
Completamos la tabla:
Calculamos el décimo término:
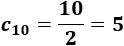
Problema 5
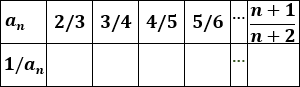
Calcular el término general \(1/a_n\) de la inversa de la sucesión, completar la siguiente tabla y calcular el décimo término de la inversa:
Ver solución
Calculamos el término general de la inversa:
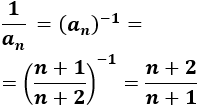
Completamos la tabla:
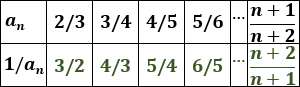
Calculamos el décimo término:
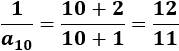
Problema 6
Sean las sucesiones
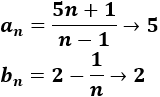
Calcular los límites de
-
La suma \(a_n+b_n\).
-
La resta \(a_n-b_n\).
-
El producto \(a_n·b_n\).
-
El cociente \(a_n/b_n\).
Ver solución
Las dos sucesiones son convergentes a números distintos de 0, así que conocemos la convergencia de las operaciones sin calcular las operaciones.
Problema 7
Vimos en un ejemplo que
-
la sucesión \(a_n=\frac{1}{n^2}\) es convergente a 0,
-
la sucesión \(b_n=n\) es divergente y
-
el producto \(a_n·b_n=1/n\) es convergente a 0.
¿También es convergente el producto de \(a_n=1/n\) y \(b_n=n^2\)?
Ver solución
La sucesión \(a_n=1/n\) es convergente a 0 y la sucesión \(b_n=n^2\) es divergente. Sin embargo, en este caso el producto es divergente:
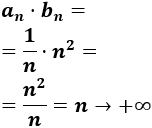
Problema 8
Sean las sucesiones
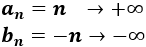
Calcular los límites de
-
La suma \(a_n+b_n\).
-
La resta \(a_n-b_n\).
-
El producto \(a_n·b_n\).
-
El cociente \(a_n/b_n\).
Ver solución
Como las dos sucesiones son divergentes, tendremos que calcular las operaciones para estudiar la convergencia de las sucesiones.
-
La suma es convergente por ser constante:
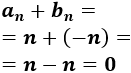
-
La resta es divergente:
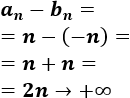
-
El producto es divergente:
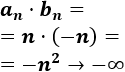
-
El cociente es convergente por ser constante:
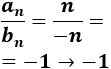
Problema 9
Calcular el límite de la inversa de las siguientes sucesiones:
-
\( a_n=1/n\rightarrow 0 \)
-
\(b_n=5+1/n\rightarrow 5\)
-
\(c_n=7n\rightarrow +\infty \)
Ver solución
-
Calculamos el límite de \(1/a_n\):
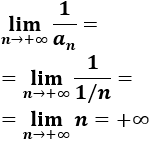
-
Como el límite de la sucesión es \(5\neq 0\), el límite de la inversa es 1/5:
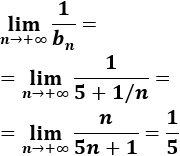
-
Calculamos el límite de \(1/c_n\):
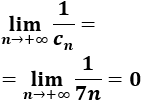
Problema 10
Sean las sucesiones
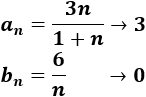
Calcular los límites de
-
La suma \(a_n+b_n\).
-
La resta \(a_n-b_n\).
-
El producto \(a_n·b_n\).
-
El cociente \(a_n/b_n\).
Ver solución
Las dos sucesiones son convergentes.
-
La suma converge a 3.
-
La resta converge a 3.
-
Como una de las sucesiones converge a 0 y la otra no diverge, el producto converge a 0:
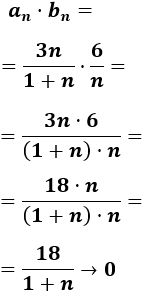
-
El cociente diverge:
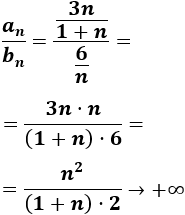
El límite es infinito porque el grado del numerador es mayor que el del denominador.