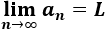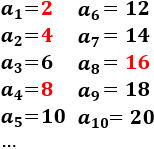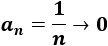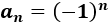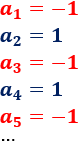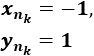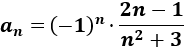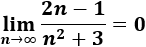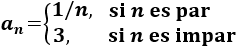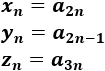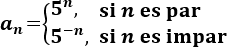Problema 1
Sea la sucesión \(a_n\) convergente a 0 dada por
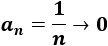
Sus primeros términos son: 1, 1/2, 1/3, 1/4,...
Determinar si las siguientes sucesiones son subsucesiones de \(a_n\):
-
\( a_{n_k} = \frac{1}{2k} \rightarrow 0\)
-
\( a_{n_k} = 1-\frac{1}{k} \rightarrow 1\)
-
\( a_{n_k} = \frac{1}{k^2} \rightarrow 0\)
-
\( a_{n_k} = \frac{2}{k} \rightarrow 0\)
-
\( a_{n_k} = \frac{1+k}{k^2} \rightarrow 0\)
Ver solución
-
\( a_{n_k} = \frac{1}{2k} \rightarrow 0\)
Los primeros términos son 1/2, 1/4, 1/8,... Es una subsucesión de \(a_n\).
-
\( a_{n_k} = 1-\frac{1}{k} \rightarrow 1\)
No es una subsucesión de \(a_n\) porque converge a 1. Sus primeros términos son 0, 1/2, 2/3, 3/4,...
-
\( a_{n_k} = \frac{1}{k^2} \rightarrow 0\)
Los primeros términos son 1, 1/4, 1/9, 1/16,... Es una subsucesión de \(a_n\).
Las dos siguientes sucesiones no son subsucesiones de \(a_n\) porque, por ejemplo, el primer término de ambas es 2, pero 2 no es un término de \(a_n\).
-
\( a_{n_k} = \frac{2}{k} \rightarrow 0\)
Sus primeros términos son 2, 1, 2/3, 1/2, 2/5,...
-
\( a_{n_k} = \frac{1+k}{k^2} \rightarrow 0\)
Sus primeros términos son 2, 3/4, 4/9,...
Problema 2 (dificultad media)
Dada una sucesión \(a_n\), construimos la sucesión constante \(x_n = a_1\). ¿Es \(x_n\) una subsucesión de \(a_n\)?
Ver solución
No. La sucesión \(x_n\) no es una subsucesión de \(a_n\) porque no es un conjunto formado por los términos de \(a_n\) con índice de un subconjunto de los naturales de cardinalidad infinita.
La sucesión \(a_n\) sólo puede tener una subsucesión constante igual a \(k\) si existen infinitos términos de \(a_n\) que sean iguales a \(k\).
Problema 3
Sea la sucesión alternada \(a_n\) dada por
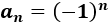
Demostrar que no converge a partir de sus subsucesiones.
Ver solución
La sucesión es alternada y sus primeros términos son
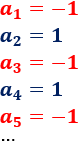
Sean las subsucesiones
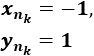
Son sucesiones convergentes porque son constantes, pero sus límites son distintos. Por tanto, \(a_n\) no converge.
Problema 4
Sea la sucesión alternada dada por
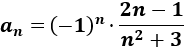
Calcular el límite de las siguientes subsucesiones de \(a_n\):
-
\( x_n = a_{2n}\)
-
\( y_n = a_{2n+1} \)
-
\( z_n = a_{n^2}\)
Ver solución
La sucesión \(a_n\) es alternada, pero es convergente a 0 ya que la fracción tiende a 0:
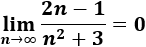
Los términos de \(a_n\) van cambiando de signo, pero aproximándose a 0.
Como consecuencia de la convergencia de \(a_n\), todas las subsucesiones de \(a_n\) convergen también a 0.
Problema 5
Sea la sucesión no convergente definida por
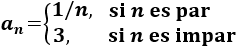
Proporcionar tres subsucesiones \(x_n\), \(y_n\) y \(z_n\) tales que
-
\(x_n\) e \(y_n\) son convergentes con límites distintos.
-
\(z_n\) no es convergente.
Demostrar como consecuencia que la sucesión \(a_n\) no converge.
Ver solución
Sean las subsucesiones
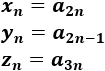
La subsucesión \(x_n\) converge a 0 (son los términos de \(a_n\) con posición par).
La subsucesión \(y_n\) converge a 3 (son los términos de \(a_n\) con posición impar).
La subsucesión \(z_n\) no converge (tiene términos con posición par e impar de \(a_n\): \(a_3\), \(a_6\), \(a_9\),...).
La sucesión \(a_n\) no converge porque tiene dos subsucesiones convergentes a límites distintos.
Problema 6 (dificultad media)
Sea la sucesión definida por
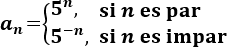
Determinar si las siguientes sucesiones son subsucesiones de \(a_n\):
-
\( x_n = 5\)
-
\( y_n = 5^n\)
-
\( z_n = 5^{-n}\)
-
\( t_n = 5^{n^2}\)
-
\( u_n = 5^{2n^2}\)
Ver solución
-
\( x_n = 5\)
No lo es (Problema 2).
-
\( y_n = 5^n\)
No es subsucesión porque los términos de \(y_n\) con posiciones impares no están en la sucesión \(a_n\).
-
\( z_n = 5^{-n}\)
No es subsucesión porque los términos de \(z_n\) con posiciones pares no están en la sucesión \(a_n\).
-
\( t_n = 5^{n^2}\)
No es subsucesión porque los términos de \(t_n\) tales que \(n^2\) es un número impar no están en la sucesión \(a_n\).
-
\( u_n = 5^{2n^2}\)
Sí es una subsucesión porque el exponente \(2n^2\) es par y, por tanto, los términos de \(u_n\) son términos de \(a_n\).